1. Методика построения матрицы планирования многофакторного эксперимента типа пфп – 22 для исследования оперативно-тактических действий пожарных подразделений при дублировании опытов.

Помимо варьируемых факторов на объект исследования всегда воздействуют различные неконтролируемые факторы (шумы), что приводит к уменьшению точности результатов эксперимента. Влияние мешающих факторов можно в известной степени уменьшить, если каждый опыт экспериментального плана повторять (дублировать) некоторое число раз. Та­кой эксперимент называется экспериментом с дублированными, или с параллельными опытами.

При равномерном дублировании опытов ПФП матрица планирования не теряет своих оптимальных свойств (11.5)-(11.7).

(11.5)

где x_ij - значение i-го фактора в j- м опыте;

i =1, 2, ..., k; j = 1,2, ..., N;

N- число основных опытов.

Нормированность - сумма квадратов элементов столбца любого фактора равна числу опытов:

(11.6)

Ортогональность - сумма почленных произведений любых двух столбцов матрицы равна нулю:

(11.7)

Матрицы планирования, обладающие этими свойствами, называют ортогональными.

Кроме того, сохраняются в силе формулы (11.9), (11.10), (11.19)

(11.9)

(11.10)

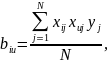(11.19)

для вычисления коэффициентов регрессии, с той лишь разницей, что в качестве выходной величины j-и серии y_j, (j = 1,2, ...,N) следует брать ее среднее арифметическое _j, по всем дублированным опытам этой серии:

, (11.20)

где n - число дублированных опытов в каждой серии

Отметим, что необходимыми предпосылками правильности дальнейшей статистической обработки результатов эксперимента являются нормальность распределения выходной величины эксперимента и однородность дисперсий опытов.

2. Роль коэффициента Стьюдента в изучении параметров оперативно тактических действий пожарных подразделений. Привести примеры.

Проверять нулевую гипотезу относительно средних ₁ и ₂двухвыборок можно, только если соответствующие оценки дисперсийS₁²и S₂²однородны. Поэтому проверке нулевой гипотезы относительно средних должна предшествовать проверка однородности оценок дисперсий этих выборок.

Проверка нулевой гипотезы относительно двух выборочных средних ₁ и ₂производится следующим образом.

После проверки однородности оценок дисперсийS₁²и S₂²находят:

(8.28)

и суммарное число степеней свободы

f = f₁ + f₂, (8.29)

где f₁иf₂ - число степеней свободы первой и второй выборок соответственно.

Далее рассчитывают значение величины t_расч:

(8.30)

По табл. п 2 Приложения для данного числа степеней свободыfи уровня значимостиq находят значение t_табл. Величина t_табл показывает, какое наибольшее значение может принять величина t_расчпри условии, что нулевая гипотеза о равенстве двух выборочных средних справедлива. Следовательно, если t_pасч<t_табл, принимают гипотезу о том, что ₁ и ₂ являются оценками одного и того же генерального среднего (математического ожидания)М_у, то есть расхождение между ₁ и ₂несущественно (незначимо).

Изложенная процедура проверки нулевой гипотезы о двух выборочных средних называется проверкой по t - критерию Стьюдента.

Билет 6