1. Технология оперативно-тактических действий по развертыванию насосно-рукавных систем по транспортированию раствора и подачи пены.

Раствор пенообразователя в воде для получения в воздушно механической пены можно подавать насосной установкой МСП, емкость которого заполнен пенообразователем. Воздушно-механическую пену можно подавать с использованием МСП, емкости, которых не заполнены пенообразователем. В этом случае пеносмеситель забирает пенообразователь из посторонней емкости.

Иногда емкость для воды автоцистерны заполнена раствором воды и пенообразователя. Тогда не следует включать в работу пеносмеситель. Раствор, попадая в насос, подается последним по рукавной линии к воздушно-пенному стволу.

При развертывании отделения для транспортирования раствора ПО в воде и подачи воздушно-механической пены обязанности пожарного расчета остаются такими же, как при развертывании НРС для транспортирования и подачи воды. Только к обязанностям добавляются действия по работе с оборудованием для пенообразования.

Работая на насосной установке с пеносместиелем, необходимо знать, что:

- при задействовании насосной установки для получения воздушно-механической пены исключается подача чистой воды;

- при заборе воды из водопровода давление у всасывающего патрубка должно быть не более 1/3 давления развиваемого насосом МСП;

- при нормальной работы воздушно-пенных стволов напор у ствола должен быть не менее 40-60 м. Поэтому напор на насосе должен быть равен напору у ствола плюс потери напора на сопротивление в рукавной линии и рукавной арматуре.

После окончания работы пеносмесителя необходимо тщательно промыть пенные коммуникации.

Алгоритм действий пожарного расчета при подаче пены, определяется рабочей документацией на МСП.

При недоступных подъездах к водоисточнику рекомендуется мотопомп или мотонасосов, использовать для забора воды и ее транспортировке к указанным местам.

2. Методика определения коэффициентов уравнения регрессии при проведении экспериментов с дублированными опытами при планировании дробного многофакторного эксперимента типа 2 к-1.

11.4 Проведение эксперимента с дублированными опытами

Помимо варьируемых факторов на объект исследования всегда воздействуют различные неконтролируемые факторы (шумы), что приводит к уменьшению точности результатов эксперимента. Влияние мешающих факторов можно в известной степени уменьшить, если каждый опыт экспериментального плана повторять (дублировать) некоторое число раз. Та­кой эксперимент называется экспериментом с дублированными, или с параллельными опытами.

При равномерном дублировании опытов ПФП матрица планирования не теряет своих оптимальных свойств (11.5)-(11.7). Кроме того, сохраняются в силе формулы (11.9), (11.10), (11.19) для вычисления коэффициентов регрессии, с той лишь разницей, что в качестве выходной величины j-и серии y_j, (j = 1,2, ...,N) следует брать ее среднее арифметическое _j, по всем дублированным опытам этой серии:

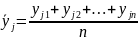, (11.20)

где n - число дублированных опытов в каждой серии

Отметим, что необходимыми предпосылками правильности дальнейшей статистической обработки результатов эксперимента являются нормальность распределения выходной величины эксперимента и однородность дисперсий опытов.

11.5 Обработка результатов эксперимента при

равномерном дублировании опытов

В случае равномерного дублирования опытов результаты эксперимента обрабатываются в такой последовательности.

1. Вычисляются средние арифметические выходных величин по каждой серии дублированных опытов (см. формулу (11.20). Результаты расчетов записывают во 2-й столбец табл.11.7

2. Вычисляют коэффициенты регрессии (для ПФП см. формулы (11.9), (11.10), (11.19). В этих формулах вместо у_j, следует взять средние значение _j по каждой серии дублированных опытов. Записать полученную математическую модель.

В найденное уравнение регрессии (в нормализованных обозначениях факторов) подставляются значения факторов х₁, х₂, ..., х_n, соответствующие условиям 1-го, 2-го, ..., N-го опытов. (Здесь N - число серий дублированных опытов). Таким образом, вычисляются значения выходной величины ŷ₁, ŷ₂ , …, ŷ_N предсказанные уравнением регрессии для каждого из опытов. Например, для уравнения регрессии (11.11), найденного в результате реализации ПФП 2² (табл.11.3), имеем:

ŷ₁ = b₀ + b₁(+1) + b₂(-1); (11.20)

ŷ₂ = b₀ + b₁(-1) + b₂(-1) и т. д. (11.21)

Результаты расчетов записывают в 3-й столбец табл.11.7.

Вычисляют оценки дисперсии для каждой серии дублированных опытов по формуле

(11.22)

где n - число дублированных опытов в каждой серии (n = 4 для ПФП в табл. 11.7);

у_ji.. - значение выходной величины в i-м дублированном опыте j-й серии;

j=1,2,...,N; i = 1,2, ...,п.

Для расчетов удобнее использовать второе выражение.

Результаты расчетов записывают в 4-й столбец таблицы.

Проверяют однородности дисперсий опытов по критерию Кохрена. Вычисляют оценку дисперсии, характеризующей ошибку экспе­римента, S²{у}. Она является средним арифметическим оценок дисперсий дублированных опытов:

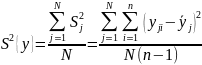( 11.23)

Для расчетов удобнее использовать первое выражение.

Число в знаменателе формулы (11.23)

f_y = N(n-1) (11.24)

представляет собой число степеней свободы, связанное с оценкой дисперсии S²{у}.

Вычисляют оценки дисперсий коэффициентов регрессии. Коэффициенты регрессии b_i, b_ji являются случайными величинами. Оценки дисперсий коэффициентов регрессии характеризуют точность, с которой они найдены. Для ПФП оценки дисперсий всех коэффициентов равны друг другу и определяются по формуле

(11.25)

Оценивают значимости коэффициентов регрессии. Эта процедура позволяет выявить незначимые факторы или их взаимодействия, приравняв к нулю коэффициенты при соответствующих факторах или их взаимодействиях.

Коэффициенты регрессии оказываются незначимыми в том случае, если соответствующий ему фактор или взаимодействие оказывает пренебрежимо малое влияние на изменение выходной величины объекта исследования.

Оценка значимости коэффициентов регрессии проводится с помощью t-критерия Стьюдента в следующем порядке:

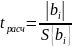(11.26)

а) для каждого коэффициента регрессии b_i, вычисляется расчетное t-отношение:

где S {b_i} - среднеквадратическое отклонение коэффициента b_i, равное корню из его оценки дисперсии;

б) из таблиц t-распределения (см. табл. Приложения 1 ) по величине f_y для уровня значимости q = 0,05 берётся табличное t-отношение t_табл;

в) проверяется условие t_pacч ≤ t_табл. Коэффициенты регрессии, для которых это условие выполняется, являются незначимыми.

Незначимые коэффициенты регрессии исключаются из математической модели.

Билет 5