19(2) Методика определения количества измерений и интервалов между измерениями при исследовании оперативно – тактических действий.

Определив доверительный интервал, мы тем самым определяем точность, с которой выборочное среднее совпадает с генеральным средним М_у. Можно поставить и обратную задачу: найти такой объем выборки n_р, чтобы вероятность р отклонения выборочного среднего от генерального среднего М_у на величину, большую Δ, была достаточно мала. Надежность полученного таким образом результата (уровень достоверности) будет равна:

p = 1-q

Например, мы хотим, чтобы вероятность отклонения выборочного среднего от генерального среднего М_у = 36,6 с (см. пример из предыдущего пункта) на величину, большую Δ = 3 с, была равна 0,01. Отклонение выборочного среднего от действительного на величину больше 3 с при этих условиях наблюдалось бы только в одном случае из 100. Спрашивается, сколько наблюдений и мы должны произвести, чтобы это условие выполнялось?

Выборка, которая с достаточной точностью представляет параметры генеральной совокупности, называется представительной, или репрезентативной.

Для определения объема репрезентативной выборки предварительно ставится серия наблюдений объемом n. Число n опытов предварительной серии наблюдений определяется априорной информацией о степени изменчивости изучаемой величин (при исследовании оперативно-тактических действий число n рекомендуется брать порядка 50-150).

По результатам серии предварительных опытов необходимо:

Вычислить выборочное среднее и выборочную дисперсию S²;

Найти объем n_р репрезентативной выборки по формуле:

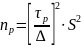
Величина Δ представляет собой абсолютную допускаемую ошибку определения среднего значения выборки. Относительно допускаемая ошибка ε будет равна

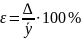
Если при определении объема репрезентативной выборки требуется учитывать относительную ошибку, то следует использовать формулу

где υ- коэффициент вариации.

Формулы справедливы и в том случае, если объем n серии предварительных опытов невелик (n< 120).

Чтобы проверить, является ли выборка из n_р наблюдений действительно репрезентативной, нужно найти доверительный интервал для выборочного среднего , полученного из этой выборки.

Порядок оценки основных параметров статистической совокупности

• Принять длину h интервалов статистического ряда в нашем примере равной 100 (табл. 8.2)

определить, их количество к по формуле:

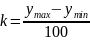
где y_min - наименьшее значение случайной величины;

y_max - ее наибольшее значение.

При этом значение y_min берется на 100 единиц меньше минимального оцифрованного значения шкалы, а y_max - на 100 единиц больше максимального оцифрованного значения шкалы.

• По образцу табл. 8.2 подготовить рабочую таблицу. В первый столбец этой таблицы заносят номера i = 1, 2...,к интервалов, на которые разбит весь диапазон изменения случайной величины. Во втором столбце указаны нижние у_iн и верхние у_iв- границы этих интервалов. В третий столбец таблицы заносят срединное значение у_i* каждого i-го интервала:

Рабочая таблица облегчает построение статистического ряда. Она заполняется непосредственно во время проведения эксперимента. Случайная величина, попавшая в какой-либо интервал, отмечается в четвёртом столбце таблицы точкой. Таким образом, каждая точка соответствует одному значению случайной величины, попавшей в данный интервал. По окончании эксперимента количество точек в каждом интервале суммируют и определяют частоту р_i, попадания случайной величины в каждый i-й интервал.

Для удобства подсчета числа попаданий в интервал ис­пользуют метод точкования. В соответствии с этим методом первые 4 попадания случайной величины в интервал последовательно отмечаются точками, расположенными в вершинах квадрата . Следующие 4 попадания отмечают черточками, образующими стороны квадрата и, наконец, 9-е и 10-е попадания отмечаются черточками, образующими диагонали квадрата . Полученная в результате фигура соответствует десяти попаданиям в i-й интервал.

Если случайная величина попадает на границу двух интервалов, включить ее в интервал с большим номером.