Билет 1

1. Методика сравнения средних двух статистических выборок при изучении оперативно-тактических действий. Привести пример. Проверять нулевую гипотезу относительно средних ₁ и ₂двухвыборок можно, только если соответствующие оценки дисперсийS₁²и S₂²однородны. Поэтому проверке нулевой гипотезы относительно средних должна предшествовать проверка однородности оценок дисперсий этих выборок.

Проверка нулевой гипотезы относительно двух выборочных средних ₁ и ₂производится следующим образом.

После проверки однородности оценок дисперсийS₁²и S₂²находят:

(8.28)

и суммарное число степеней свободы

f = f₁ + f₂, (8.29)

где f₁иf₂ - число степеней свободы первой и второй выборок соответственно.

Далее рассчитывают значение величины t_расч:

(8.30)

По табл. п 2 Приложения для данного числа степеней свободыfи уровня значимостиq находят значение t_табл. Величина t_табл показывает, какое наибольшее значение может принять величина t_расчпри условии, что нулевая гипотеза о равенстве двух выборочных средних справедлива. Следовательно, если t_pасч<t_табл, принимают гипотезу о том, что ₁ и ₂ являются оценками одного и того же генерального среднего (математического ожидания)М_у, то есть расхождение между ₁ и ₂несущественно (незначимо).

Изложенная процедура проверки нулевой гипотезы о двух выборочных средних называется проверкой по t - критерию Стьюдента.

2. Методика построения уравнения регрессии для двух переменных факторов с помощью графоаналитического метода при изучении параметров тушения пожаров.

При применении графоаналитического метода для установления уравнений регрессии на графике в системе координат с равными шкалами изображается зависимость от одного фактора при постоянных значениях других факторов.

Если расположение точек при нанесении их на график указывает, что зависимость носит прямолинейный характер, то нормативная линия выражается уравнением:

Y=a x+b₀, (10.8)

где у и х – значения зависимой и независимой переменных на оси ординат и абсцисс

а- угловой коэффициент прямой, равный численному значению тангенса угла наклона прямой к положительному направлению оси абсцисс;

b₀- свободный член уравнения, численно равный отрезку, отсекаемому прямой на оси ординат.

Если расположение точек на графике в системе координат равномерными шкалами приближается к кривой линии, то зависимость будет носить степенной характер и выражается уравнением:

Y=b₀ xⁿ, (10.9)

Где n- показатель степени, равный численному значению тангенса угла наклона нормативной линии к положительному направлению оси абсцисс.

В системе координат с логарифмическими шкалами уравнение вида изображается прямой линией. Для определения координат нормативной линии в системе координат с логарифмическими шкалами необходимо уравнение прологарифмировать, и оно примет вид:

, (10.10)

Где y₁=lgy, b₁=lgb₀ и x₁=lgx.

Определение параметров уравнения регрессии осуществляется в следующей последовательности:

Находиться среднеарифметическое значение независимого переменного факторов – х_ср и y_ср; все факторы разбиваются на две группы, в первую включаются факторы, имеющие значения x<x_ср, а во вторую все значения x>x_ср. Для каждой группы находиться среднеарифметическое значения х и и и соответствующие и ;

определяется на основе полученных данных тангенса угла наклона нормативной линии, которой численно равен угловому коэффициенту нормативной линии (а) или показатель степени (n)

(10.11)

- Греческая буква алфавита

Свободный член уравнения определяется непосредственно из уравнения Y=a x+b₀, преобразовать его в вид b₀= y- a x,

Где х- численно равный среднеарифметическому значению независимых переменных (x_ср);

y- численно равный среднеарифметическому значению независимых переменных (y_ср).

Если затраты времени зависят одновременно от двух факторов (Y₁=a₁ x+b₁, и Y₂=a₂ z+b₂), то общая зависимость затрат времени о факторов выражается уравнением:

Y₁=a₁ x+a₂ z+b₀ (10.12)

При этом свободный член определяется по формуле:

(10.13)

Где – постоянное значение x, при котором изучалось влияние на y измерений;

- постоянное значение z, при котором изучалось влияние на измерений x;

Билет 2

1. Методики сравнения средних двух статистических выборок, полученных при исследовании оперативно-тактических действий.

Поставить две серии опытов в одинаковых условиях (по n опытов в каждой серии). Результаты первой серии опытов заносить во второй столбец табл.8.7, второй серии в четвертый столбец.

Таблица 8.7

• По формуле (8.40) найти значение выборочных средних ₁и ₂

для каждой из выборок:

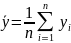(8.40)

Гдеп - число опытов;

y_i- результат i-го опыта.

• По формуле (8.41) найти оценки дисперсийS₁²иS₂²для каждой из выборок:

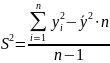(8.41)

• Проверить гипотезу об однородности двух выборочных сред них ₁и ₂. Для этого:

а) по формуле (8.43) найти среднюю оценку дисперсии

(8.43)

б) по формуле (8.44) найти значение t_расч:

(8.44)

в) сравнить найденное значениеt_расч с полученным значением t_табл;

г) если t_расч≤t_табл принять гипотезу об однородности выборочных средних ₁и ₂, В противном случае нулевую гипотезу следует отвергнуть.

• Проанализировать полученные результаты. Сделать выводы: для средних значений обеих серий опытов справедлива /несправедлива нулевая гипотеза. Между ними нет существенного различия /имеется существенное различие.