3.2 Стадии напряж-дефор состояния жбэ
Три стадии напряженно-деформированного состояния железобетонных элементов.
Опыты с различными железобетонными элементами - изгибаемыми, внецентренно
растянутыми, внецентренно сжатыми с двузначной эпюрой напряжений показали, что при
постепенном увеличении нагрузки можно наблюдать 3 характерные стадии напряженно -
деформированного состояния:
стадия 1 - до появления в бетоне растянутой зоны трещин, когда напряжения в бетоне
меньше временного сопротивления растяжению и растягивающие усилия воспринимаются
арматурой и бетоном совместно;
стадия II - после появления трещин в бетоне растянутой зоны, когда растягивающие
усилия в местах, где образовались трещины, воспринимаются арматурой и участком бетона
над трещиной, а на участках между трещинами - арматурой и бетоном совместно;
стадия III - стадия разрушения, характеризующаяся относительно коротким периодом
работы элемента, когда напряжения в растянутой стержневой арматуре достигают физического
или условного предела текучести, а в высокопрочной проволоке - временного сопротивления, а
напряжения в бетоне сжатой зоны - временного сопротивления сжатию. В зависимости от
степени армирования элемента последовательность разрушения зон - растянутой и сжатой может изменяться.
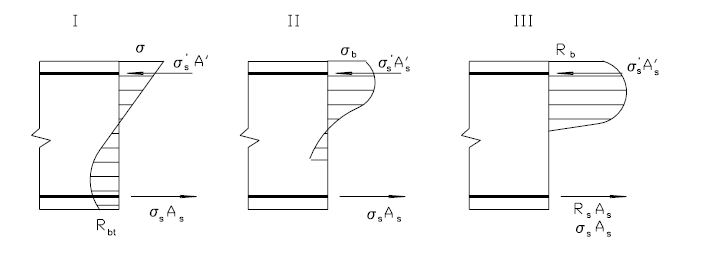
Стадия II. В том месте растянутой зоны, где образовались трещины, растягивающее
усилие воспринимается арматурой и участком бетона над трещиной. В интервалах между
трещинами в растянутой зоне сцепление арматуры с бетоном сохраняется, и по мере удаления
от краев трещин растягивающие напряжения в бетоне увеличиваются, а в арматуре -
уменьшаются. С дальнейшим увеличением нагрузки на элемент в бетоне сжатой зоны
развиваются неупругие деформации, эпюра нормальных напряжений искривляется, а ордината
максимального напряжения перемещается с края сечения в его глубину. Конец стадии II
характеризуется началом заметных неупругих деформаций в арматуре.
Стадия I. При малых нагрузках на элемент напряжения в бетоне и арматуре невелики,
деформации носят преимущественно упругий характер; зависимость между напряжениями и
деформациями - линейная, эпюры нормальных напряжений в бетоне сжатой и растянутой зон
сечения - треугольные. С увеличением нагрузки на элемент в бетоне растянутой зоны
развиваются неупругие деформации, эпюра напряжений становится криволинейной,
напряжения приближаются к пределу прочности при растяжении. Этим характеризуется конец
стадии 1. При дальнейшем увеличении нагрузки в бетоне растянутой зоны образуются
трещины, наступает новое качественное состояние.
3.3.1 Метод расчета по допускаемым напряжениям.
Метод расчета прочности сечений изгибаемых элементов по допускаемым напряжениям
исторически сформиовался первым; в нем за основу взята стадия II напряженно -
деформированного состояния и приняты следующие допущения: бетон растянутой зоны не работает, растягивающее напряжение воспринимает арматура; бетон сжатой зоны работает упруго, а зависимость между напряжениями и деформациями - линейная согласно закону Гука; нормальные к продольной оси сечения, плоские до изгиба, остаются плоскими после изгиба (гипотеза плоских сечений).
Как следствие этих допущений, в бетоне сжатой зоны принимается треугольная эпюра
напряжений (рис. 2.3) и постоянное отношение модулей упругости материалов. Рассматривают приведенное однородное сечение, в котором площадь сечения растянутой арматуры заменяют площадью сечения бетона, равной αАs. Исходя из равенства деформаций бетона и арматуры
σs = ασb.
Краевое напряжение в бетоне
σb = Mx/Ired;
Напряжения в растянутой арматуре
σs = αM(ho- x)/Ired;
Напряжения в бетоне и арматуре ограничивают допускаемыми напряжениями, которые
устанавливают, как некоторые доли временного сопротивления бетона сжатию
σb = 0.45R (марка бетона, принимаемая равной кубиковой прочности бетона) и предела
текучести арматуры
σs = 0.5σy;
Основной недостаток метода расчета сечений по допускаемым напряжениям
заключается в том, что бетон рассматривается как упругий материал. Действительное же
распределение напряжений в бетоне по сечению в стадии II не отвечает треугольной эпюре напряжений, а отношение модулей упругости число переменное, зависящее от значений напряжений в бетоне, продолжительностиего действия и других факторов. Как результат, напряжение в арматуре меньше вычисленных. Это приводит к излишнему расходу материалов, требует установки арматуры в местах, где она не используется и т.д.