Расчет параллельно соединенных трубопроводов

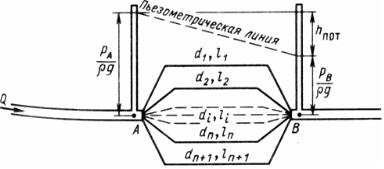
Параллельно соединенные трубопроводы относятся к сложным системам. Схема параллельно соединенного трубопровода представлена на рис.. Пусть в точке A трубопровод разветвляется, а в точке В его ветви сходятся.

Длина и диаметр каждой ветви соответственно обозначены l₁, l₂,... l_n+1 и d₁, d₂,... d_n+1.

Потери напора в каждой ветви одинаковы и равны H=h_w, так как концы ветвей смыкаются в точках А к В, в каждой из которых может быть только один напор; кроме того, сумма расходов отдельных ветвей равна магистральному или общему расходу. Исходя из этого, напишем расчетные уравнения для потери напора:

для первой ветви hw = Q 1₂ l₁ /K₁² 

для второй ветви hw = Q ₂²l₂ /K²² 

для n-й ветви hw = Q _n² l_n /K_n² 

Получается всего n уравнений, в которых содержитcя n+1 неизвестных, в том числе n неизвестных расходов плюс потери напора hw. Чтобы найти все неизвестные, надо иметь еще одно уравнение. Напишем уравнение неразрывности для угловых точек А или В т. е.

Q=Q₁ +Q₂ +…+Q_n

Имея n+1 уравнений, можно определить все неизвестные. Расходы определяются по отдельным ветвям в соответствии с зависимостью

Q₁/Q₂=K₁/K₂ =.

Отсюда

Q₂=Q₁ ,

Q_n=Q₁ ,

Тогда

Q₁=Q/(1+ +…+ ).

47. Сложные трубопроводы

Длинные трубопроводы – это трубопроводы, у кото­рых местные потери напора незначительны и не превышают 5-10% от потерь напора по длине, к ним относятся водо­проводы, участки магистральных нефтепроводов. При расчете длинных трубопроводов находят потери напора по длине hл, затем увеличивают их на 5-10%.

При расчете длинных трубопроводов местными сопротивлениями и скоростным напором на выходе пренебрегают и уравнение приобретает вид:

H=h _л= λl/d *v²/2g

Т.е. напор в трубопроводе равен сумме потерь напора по длине, определяемых по формуле Дарси-Вейсбаха.

Запишем формулу относительно скорости в трубопроводе, подставив в нее диаметр трубы, выраженный через гидравлический радиус d = 4R, и гидравлический уклон i=h_л /l.

v= * , обозначив С= , получим формулу Шези

v=С * .

Расход в трубопроводе определяется по формуле:

Q=vw=wC .

Произведение wC обозначают буквой К и называют расходной характеристикой трубопровода, тогда уравнение имеет вид

Q=K .

Размерность К такая же, как и расхода. Численно значение равно расходу при уклоне, равном единице.

Величина 1/K² = А называется удельным сопротивлением.

Потери напора по длине с помощью этих параметров выражаются

hл=AlQ²=lQ²/K².

Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).

Рис. 6.6. Схемы сложных трубопроводов

Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q _B и Q_D и Q_E .

Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках P_B и P_D и P_E.

Для этого случая возможны два вида задач:

Задача 1. Дан расход Q в основной магистрали M_A. Необходимо определить расходы Q_B и Q_D и Q_E, а также потребный напор в точке М.

Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.

Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:

уравнение расходов:

Q = Q_B = Q_D = Q_E

уравнение равенства потребных напоров для ветвей CD и CE

H_{ст D} + K_CDQ_D^т = H_{ст E} + K_CEQ_E^т

уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD

H_{ст B} + K_ABQ_B^т = H_{ст D} + K_CDQ_D^т + K_AC(Q_D + Q_E)^т

выражение для потребного напора в точке М

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых; 2) строят кривые потребных напоров для каждого из простых трубопроводов; 3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов; 4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).

Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.