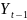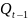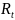Задача 44
Для
линейного уравнения регрессии
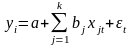
(m
- число независимых переменных уравнении)
исследуйте остатки на наличие
автокорреляции на уровне значимости
 ,
используя тест Дарбина-Уотсона,
если известны значения
,
используя тест Дарбина-Уотсона,
если известны значения
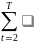 и
и
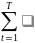 , число наблюдений равно n.
, число наблюдений равно n.
|
|
Число независимых переменных m |
число наблюдений равно n |
Уровенеь значимости
, |
0,91 |
0,97 |
4 |
18 |
0,05 |
Решение
Проверим нулевую гипотезу об отсутствии автокорреляции.
Конкурирующие гипотезы
и
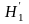 соответственно о наличии положительной
и отрицательной автокорреляции в
остатках.
соответственно о наличии положительной
и отрицательной автокорреляции в
остатках.
Рассчитаем критерий Дарбина-Уотсона по формуле:
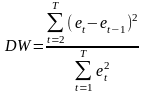
По
таблице критических точек Дарбина-Уотсона
определим
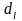 (нижнее) и
(нижнее) и
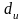 (верхнее) значения критерия
Дарбина-Уотсона для заданного
числа наблюдений
(верхнее) значения критерия
Дарбина-Уотсона для заданного
числа наблюдений
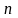 =18,
числа независимых переменных модели
m=4
и уровня значимости
=0,05.
=18,
числа независимых переменных модели
m=4
и уровня значимости
=0,05.
По
этим значениям числовой промежуток
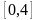 разобъём на пять отрезков:
разобъём на пять отрезков:
1).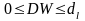 ,
2).
,
2).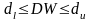 ,
3).
,
3). ,
4).
,
4).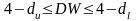 и 5)
и 5) .
.
DW
=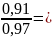 0,938
0,938
По таблице Дарбина-Уотсона для n=18 и m=4 (уровень значимости 5%) находим:
= 0,82; = 1,87
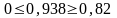
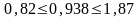
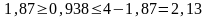

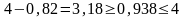
Поскольку найденное значение DW=0,938 попадает во второй интервал ( ), то можно сделать вывод , что значение попадает в так называемую зону неопределенности и не имеем возможности ни опровергнуть, ни принять ни одну из гипотез.
Задача 59
В результате
анализа динамики объёма продаж торгового
предприятия за
2001-2013гг.
было выявлено , что модель временного
ряда имеет только трендовую составляющую
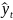 = a + b∙
t
( где t=
1,2, . . .
,14) . Сделайте точечный и интервальный
прогноз объёма продаж продукции
предприятия в момент
= a + b∙
t
( где t=
1,2, . . .
,14) . Сделайте точечный и интервальный
прогноз объёма продаж продукции
предприятия в момент
 ,
если уровень значимости равен α
, а остаточная сумма квадратов
,
если уровень значимости равен α
, а остаточная сумма квадратов
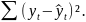
Дано
: а=14,3 млн.руб.,
b=0,1 млн.руб.,
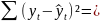 0,7,
α = 0,01,
0,7,
α = 0,01,
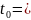 15.
15.
Решение
Точечный прогноз : . = 14,3 + 0,1∙ 14,3 + 0,1∙15 = 15,8 млн.руб.
Предельная ошибка прогноза:
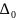 = t(n-2;
α)
∙
= t(n-2;
α)
∙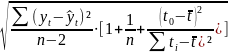
По таблице значений критерия Стьюдента найдем :
t(n-2; α) = t(12; 0.01) = 3,055
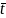 =
=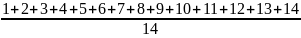 =
=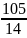 =
7,5
=
7,5
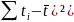 = (1-7,5)² +(2-7,5)²
+(3-7,5)² +(4-7,5)²
+(5-7,5)² +(6-7,5)²
+(7-7,5)² +(8-7,5)²
+ +(9-7,5)²
+(10-7,5)² +(11-7,5)²
+(12-7,5)² +(13-7,5)²
+(14-7,5)² =
= (1-7,5)² +(2-7,5)²
+(3-7,5)² +(4-7,5)²
+(5-7,5)² +(6-7,5)²
+(7-7,5)² +(8-7,5)²
+ +(9-7,5)²
+(10-7,5)² +(11-7,5)²
+(12-7,5)² +(13-7,5)²
+(14-7,5)² =
= 2∙ (6,5² + 5,5² + 4,5² +3,5² +2,5² +1,5² +0,5² ) = 227,5
Предельная ошибка прогноза будет равна:
=3,055 ∙
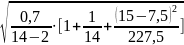 0,85
0,85
Интервальный прогноз:
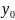 -
-
 +
+
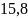 -
-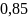
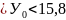 +
+
14,95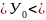 16,65
16,65
Таким образом , с вероятностью 0,95 можно утверждать, что в 2014г. объём продаж продукции будет в диапазоне от 14,95 до 16,65 млн.руб.
Задача 62
Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели .
Модель Менгеса:
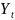 =
=
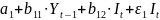 =
=
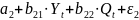
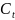 =
=

 =
=
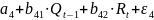 ,
,
где Y - национальный доход;
С - расходы на личное потребление;
I - чистые инвестиции;
Q - валовая прибыль экономики;
Р - индекс стоимости жизни;
R - объем продукции промышленности;
t - текущий период;
t-1 - предыдущий период.
Решение:
Модель включает
четыре эндогенные переменные (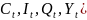 и пять предопределенные переменные
(две экзогенные переменные -
и пять предопределенные переменные
(две экзогенные переменные -
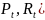 и
три лаговые эндогенные переменные -
).
и
три лаговые эндогенные переменные -
).
Проверим необходимое условие идентификации для каждого уравнения модели.
Необходимое условие идентификации (НУИ):
D+1=H - Уравнение идентифицируемо.
D+1 H - Уравнение сверхидентифицируемо.
D- число предопределенных переменных, отсутствующих в анализируемом уравнении, но присутствующих в системе;
Н- число эндогенных переменных, которые присутствуют в рассматриваемом уравнении. Предопределенные переменные - это экзогенные и лаговые переменные( за предыдущие моменты времени) эндогенные переменные.
Первое уравнение. Это уравнение включает две эндогенные переменные (Yt и It) и одну преопределенную переменную (Yt-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 4+1=5 > 2.
Уравнение сверхидентифицировано.
Второе уравнение. Это уравнение включает три эндогенные переменные (Qt, Yt и It) и ноль преопределенных переменных. Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 5+1 =6 > 3.
Уравнение сверхидентифицировано.
Третье уравнение.
Уравнение включает
две эндогенные переменные (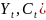 и две преопределенных переменных (Рt
и Сt-1
). Следовательно, число
предопределенных переменных, не входящих
в это уравнение, плюс 1, больше числа
эндогенных переменных, входящих в
уравнение: 3+1=4 > 1.
и две преопределенных переменных (Рt
и Сt-1
). Следовательно, число
предопределенных переменных, не входящих
в это уравнение, плюс 1, больше числа
эндогенных переменных, входящих в
уравнение: 3+1=4 > 1.
Уравнение сверхидентифицировано..
Четвёртое уравнение. Это уравнение включает одну эндогенную переменную (Qt ) и две преопределенных переменных (Rt и Qt-1 ). Следовательно, число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение: 3+1=4 > 1.
Уравнение сверхидентифицировано.
Проверим достаточное условие идентификации для каждого уравнения модели.
Достаточное условие идентификации (ДУИ):
Определитель матрицы, составленный из коэффициентов , отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы:
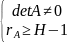
Cоставим матрицу коэффициентов при переменных рассматриваемой модели:
|
Yt |
|
It |
Qt |
Сt |
Ct-1 |
Рt |
|
|
I уравнение |
-1 |
b11 |
b12 |
0 |
0 |
0 |
0 |
0 |
0 |
II уравнение |
b21 |
0 |
-1 |
b22 |
0 |
0 |
0 |
0 |
0 |
III уравнение |
b31 |
0 |
0 |
0 |
-1 |
b32 |
b33 |
0 |
0 |
IV уравнение |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
b41 |
b42 |
Первое уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 .
.
Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:
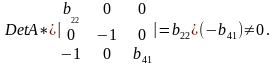 Достаточное
условие идентификации для первого
уравнения выполняется.
Достаточное
условие идентификации для первого
уравнения выполняется.
Второе уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
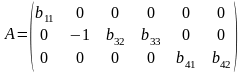
Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:
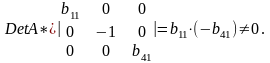
Достаточное условие идентификации для второго уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
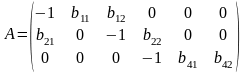 .
.
Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:
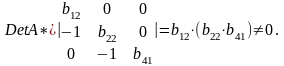
Достаточное условие идентификации для третьего уравнения выполняется.
Четвёртое уравнение.
Матрица коэффициентов при переменных,
не входящих в уравнение, имеет вид:
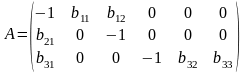 .
.
Ее ранг равен 3, так как определитель квадратной подматрицы 3 х 3 этой матрицы не равен нулю:
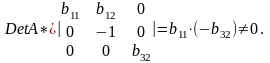
Достаточное условие идентификации для четвертого уравнения выполняется.
Все уравнения модели сверхидентифицированы.
Модель в целом является сверхидентифицируемой.