Задача 16

Зависимость объёма производства У(тыс.ед.) от численности занятых Х(чел) по 15 заводам концерна характеризуется следующим образом:

Уравнение регрессии =30 - 0,4х + 0,04х² доля остаточной дисперсии в общей 9%.

Определите: 1)индекс корреляции; 2)статистическую значимость уравнения регрессии с помощью критерия Фишера( 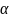= 0,05); 3) коэффициент эластичности, предполагая, что численность занятых составляет 30 человек.

Решение

Имеем уравнение нелинейной регрессии.

Общая дисперсия объясняемой переменной равна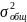 = 100 % , доля остаточной дисперсии, в общей составило 0,9, т.е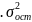 = 9%.

1) Определим индекс корреляции.

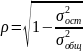= 0,954

Проверим статистическую значимость уравнения регрессии с помощью критерия Фишера на уровне значимости 0,05.

Индекс корреляции равен 0,954,тогда индекс детерминации равен R² = (0,954)² 0,91.

2)Проверяется нулевая гипотеза Hо об отсутствии нелинейной связи между переменными Х и У, т.е. R² =0 , конкурирующая гипотеза – о наличии нелинейной связи между переменными Х и У , т.е. R² 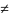0 .

Рассчитаем наблюдаемое значение критерия Фишера: n=15

= ∙ ( n -2),

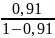= ∙ ( 15 -2) 131,4

Найдём табличное значение критерия Фишера, .

Для нашей задачи: ( ; ; α ),Степени свободы: =1, = n-2=15-2=13, уровень значимости α =0,05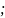

( ; ; 0,05) =4,67

Поскольку наблюдаемое значение 131,4 = > F_табл= 4,67, то нулевая

гипотеза Но об отсутствии нелинейной связи между переменными Х и У отклоняется на уровне значимости α =0,05 и принимается конкурирующая гипотеза , т.е. признаётся статистическая значимость уравнения регрессии.

3)Найдём коэффициент эластичности, предполагая, что численность занятых составляет 30 человек. Имеем уравнение полинома 2-ой степени : 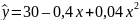Коэффициент эластичности найдём по формуле:

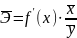
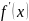= - 0,4 + 0,08х , 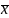= 30

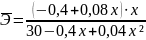= 1,11 ;

Задача 28

По 20 предприятиям региона изучается зависимость выработки продукции одного работника у (тыс.руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%).

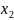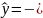1,835+0,956 + 0,086 , где 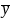= 9,6 ; 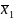= 6,19 ; 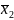= 22,3.

Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат. Ранжировать факторы по силе влияния. Найти скорректированный коэффициент детерминации, если множественный коэффициент детерминации равен 0,83.

Решение

Уравнение множественной регрессии имеет вид:

,

где 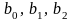– параметры модели.

Для нашей задачи имеем : 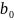= -1,835 ; 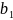= 0,956; 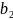= 0,086.

= 9,6 ; = 6,19 ; = 22,3 ; R² = 0,83 , n =20, р = 2.

Определим коэффициенты эластичности по формуле:

.

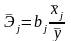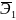= 0,956 ∙ 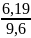0,6164 ; 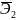= 0,086 ∙ 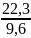0,1998

Коэффициент эластичности = 0,6164 < 1, следовательно, его влияние на результативный признак Y незначительно.

Коэффициент эластичности = 0,1998 < 1, следовательно, его влияние на результативный признак Y также незначительно.

Сравнивая значения и ранжируем Х_i по силе их влияния на У:

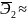а) 0,62 ; б) 0,20.

С увеличением среднего уровня ввода в действие новых основных фондов (% от стоимости фондов на конец года) (Х₁) на 1 % от его среднего уровня , средний уровень выработки продукции одного работника (У) увеличивается примерно на 0,62% от всего среднего уровня ; при повышении среднего уровня удельного веса рабочих высокой квалификации в общей численности рабочих Х₂)на 1 % , средний уровень выработки продукции одного работника (У) повышается примерно на 0,2 % от всего среднего уровня.

Таким образом , ввод в действие новых основных фондов оказывает большую силу влияния на выработку продукции одного работника , чем число рабочих высокой квалификации ( в удельном весе от общей численности рабочих).

Скорректированный коэффициент детерминации определим по формуле:

Задача 35

В результате исследования зависимости среднедневной заработной платы У от среднедушевого прожиточного минимума в день одного трудоспособного Х по n территориям региона было получено линейное уравнение регрессии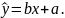 Исследуйте остатки данного уравнения регрессии на гетероскедастичность с помощью теста Голдфельда- Квандта на уровне значимости α , если остаточные суммы квадратов для первой и второй групп соответственно равны 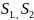; число степеней свободы остаточных сумм квадратов равны .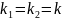

Дано: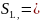 18,09; 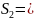95,62; ; α=0,05.

Решение

Проверяется нулевая гипотеза 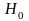об отсутствии гетероскедастичности остатков. Конкурирующая гипотеза – наличие гетероскедастичности остатков

Наблюдаемое значение критерия Фишера найдём по формуле:

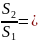
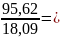= = 5,29

Найдём табличное значение критерия Фишера

( ; ; α ) = ( ; ; 0,05) =3,18.

Сравним наблюдаемое и табличное значение критерия Фишера :

Поскольку наблюдаемое значение 5,29 = > F_табл= 3,18, то нулевая

гипотеза Но об отсутствии гетероскедастичности остатков отклоняется на уровне значимости α =0,05 и принимается конкурирующая гипотеза , т.е. признаётся гетероскедастичность остатков.