2 Подготовка данных для исследования влияния демпферной обмотки на вынужденные колебания угла нагрузки

Студент исследует переходные процессы синхронного двигателя, который был спроектирован им при выполнении курсового проекта по курсу «Инженерное проектирование электромеханических устройств - Синхронные машины»

Для исследования' статической устойчивости двигателя необходимы следующие данные:

-номинальное напряжение , В

• номинальный ток 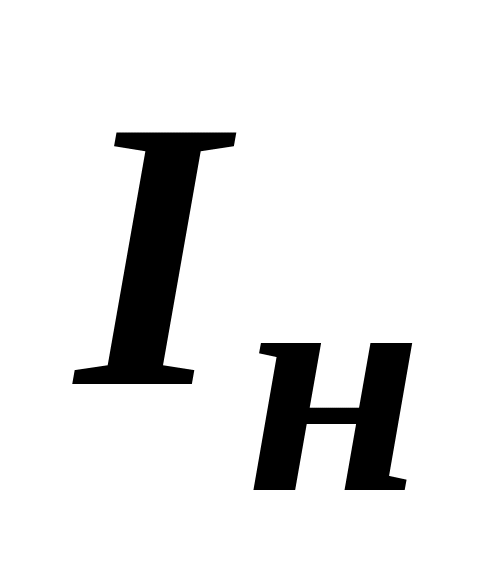, А

• число пар полюсов, ;

• перегрузочная способность двигателя 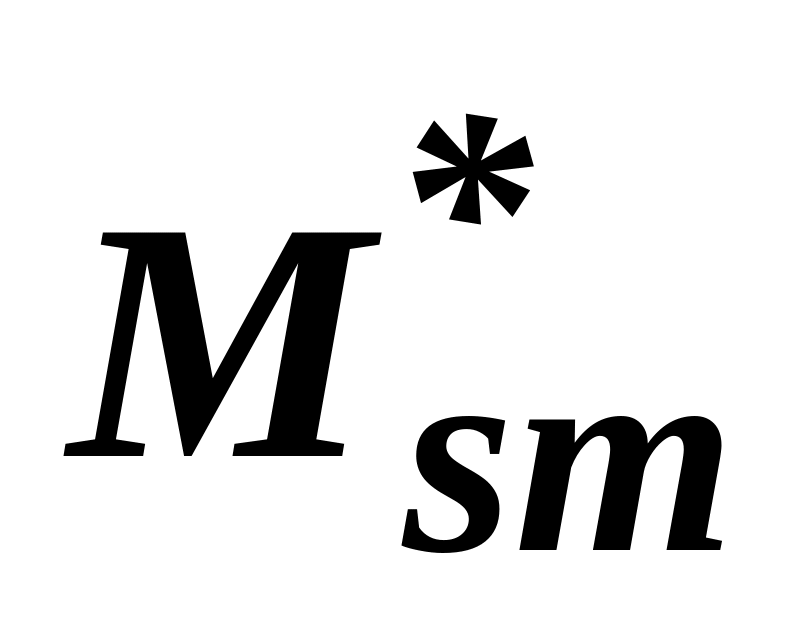, о.е.

• коэффициент нагрузки, (задается преподавателем);

• момент инерции ротора , кг м2.

Момент инерции вращающихся масс можно рассчитать

где К - коэффициент приведения момента инерции механизма к валу синхронной машины с учетом массы вала (задается преподавателем),

- масса активных материалов ротора;

где - масса меди обмотки возбуждения, кг;

- масса меди стержней пусковой обмотки, кг;

- масса меди короткозамыкающих колец, кг;

- масса стали полюсов, кг;

- масса стали обода ротора, кг;

Амплитуда гармонической составляющей момент сил сопротивления принимается равной номинальному моменту, которая в относительных единицах равна

Пример подготовки данных для построения графика изменения угла нагрузки, приведен в таблице 2.1. В качестве примера взяты данные синхронного двигателя, рассчитанного в [1].

Таблица 2.1 - Исходные данные для исследования переходных режимов

Данные курсового проекта					Рассчитываемые величины
кВт		о.е.	о.е.	о.е.	кг	кг м2	о.е.	о.е.	о.е.	о.е.	о.е.
500	6	2.2	1.98	0.2	1120	454	780	23.8	0.015	0.053	0.0358

3 Решение уравнения (1.21) средствами MathCada

Для решения дифференциального уравнения второго порядка воспользуйтесь операторным методом решения дифференциальных уравнений. Найдите изображение уравнения по методу Лапласа:

3.1 Получение уравнения (1.21) в операторной форме

Внимание. Обратите внимание на то, что для проведения замен необходимо пользоваться копированием переменных или частей уравнения, а не переписывать их. Это значительно сократить время на преобразование уравнений и позволит избежать ошибок в обозначении величин. Помните, что MathCad различает большие и малые прописные буквы.

Наберите левую часть уравнения (1.21)

• пометьте переменную

• вызовите команду "преобразование Лапласа" меню Symbolics (Символы), получите:

-введите начальные условия:

Сброс или наброс нагрузки вызывает первоначальное изменение угла нагрузки на величину . Обозначьте в уравнении (3.2): как .

Скорость изменения угла нагрузки в начальный момент переходного режима равна 0:

• введите обозначение:

- получите уравнение (1.21) в операторной форме