ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ СИНХРОННЫХ МАШИН

Лабораторная работа 4

Исследование влияния демпферной обмотки на качания ротора

синхронной машины при наличии гармонических сил

сопротивления

Цель работы: Изучить влияние демпферной обмотки на вынужденные колебания ротора синхронной машины, исследовать закон движения ротора синхронной машины с демпферной обмоткой средствами MathCAD, рассмотреть влияние демпферной обмотки на амплитуду вынужденных колебаний в зависимости от величины демпфирующего момента, от соотношения частот . Исследовать влияние демпферной обмотки на резонанс.

Программа лабораторной работы:

1. Составить математическую модель малых качаний ротора синхронной машины с демпферной обмоткой при наличии гармонических составляющих момента сил сопротивления.

2. Изучить особенности применения MathCAD для решения неоднородных дифференциальных уравнений операторным методом.

3. Составить математическую модель синхронной машины с демпферной обмоткой при наличии гармонических составляющих момента сил сопротивления;

4. Исследовать качания ротора синхронной машины с демпферной обмоткой при наличии гармонической составляющей момента сил сопротивления;

5. Построить графики изменения угла нагрузки при переходных режимах и исследовать зависимость переходных процессов:

• от частоты и амплитуды гармонической составляющей момента сил сопротивления;

• от величины демпфирующего момента;

• исследовать влияние демпферной обмотки на амплитуду вынужденных колебаний при различном соотношении частот , при резонансе.

I Основные вопросы теории, которые необходимо изучить при подготовке к отработке лабораторной работы.

1. Уравнение движения ротора

При исследовании динамической устойчивости синхронной машины угловая скорость вращения ротора является неизвестной и переменной величиной, приводящей к изменению угла нагрузки

Для получения аналитического решения при исследовании динамический устойчивости синхронной машины можно пренебречь электромагнитными переходными процессами, В этом случае можно рассматривать только механические переходные процессы с учетом только механических характеристик и уравнение движения ротора будет иметь. следующий вид.

где - момент инерции ротора, кг-м2;

- угловая скорость вращения ротора, рад/с;

- электромагнитный момент синхронной машины, Нм;

- асинхронный (демпфирующий) момент короткозамкнутой обмотки;

- момент сил сопротивления, Нм.

Следует помнить, что в электрических машинах различают геометрический угол (геометрический радиан) и электрический угол (электрический радиан). Эти углы связаны между собой зависимостью:

где - число пар полюсов.

Угловая скорость вращения ротора определяется геометрическим углом, а угол нагрузки выражается электрическими радианами. Для приведения величин к одной системе измерения углов выразим угловую скорость вращения ротора через электрические радианы, получим:

Уравнение движения ротора примет следующий вид

Для получения уравнения (1.3) в относительных единицах разделите левую и правую часть уравнения на базовый момент В этом случае все моменты уравнения (1.3) будут выражены в относительных единицах.

1.2 Динамический момент

Динамический момент возникает в результате изменения угловой скорости вращения ротора:

Выразите угловую скорость вращения ротора ω через приращение угла нагрузки и получите

Получите выражение динамического момента в относительных единицах (см. [4])

где 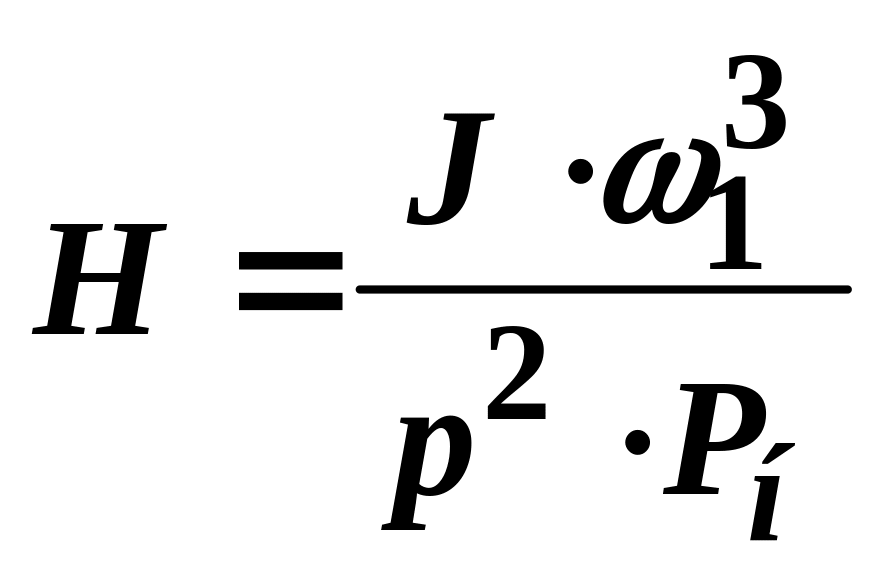- механическая постоянная вращающихся масс

1.3 Синхронизирующий момент при малых качаниях ротора

1.3.1 Синхронный электромагнитный момент

Синхронный электромагнитный момент обусловлен взаимодействием вращающегося поля якоря с главными полюсами. Рассмотрите его при условии, что реактивной составляющей синхронного момента можно пренебречь.

где - угол между осью результирующего магнитного поля в воздушном зазоре машины и продольной осью ротора;

- максимальная величина синхронного момента.

При работе двигателя с постоянной нагрузкой машина имеет постоянный угол нагрузки . При сбросе или набросе нагрузки происходит изменение угла нагрузки ( ) в результате чего возникает дополнительный синхронизирующий момент, который при малых изменениях угла нагрузки пропорционален отклонению угла от среднего значения : .

Из уравнения (1.7) следует, что дополнительный синхронизирующий момент знакопеременный (зависит от знака ), что при наличии инерционности вращающихся масс приводит к возникновению собственных незатухающих колебаний ротора, которые были изучены в [1].