22. Барометри́чна фо́рмула — формула, за якою визначають залежність тискуабо густини газу від висоти. Ця залежність зумовлена дією поля тяжіння Землі і тепловим рухом молекул газу (повітря). Припускаючи, що газ є ідеальним газом сталоїтемператури, і вважаючи поле тяжіння Землі однорідним, отримують барометричну формулу такого вигляду:

p=p0exp(−mghkT),

де p₀ — тиск на нульовому рівні (на рівні вибою в газових свердловинах, біля поверхні Землі або на рівні моря), Па;

p — тиск на висоті h, м над цією поверхнею, Па;

m — маса молекули (для повітря дорівнює масі молекули азоту), кг;

g — прискорення вільного падіння, м/с²;

k — стала Больцмана, Дж/К;

T — абсолютна температура повітря, К

Записана барометрична формула є наближеною: при виведенні її не враховано залежності g i T від висоти, відхилення газу від ідеального газу тощо. Нею можна користуватися для визначення атмосферного тиску до висоти 11 км (з поправками на зміну температури).

Барометричну формулу з певним обмеженням можна використати для визначення розподілу кількості колоїдних частинок по висоті рідинної або газової дисперсної системи, на які діє поле тяжіння. Барометрична формула є окремим випадком розподілу Больцмана.

24. Внутрішньою енергієюназивають повну енергію тіла за винятком кінетичної енергії тіла як цілого і потенціальної енергії тіла в зовнішньому полі сил. Отже, внутрішня енергія складається з кінетичної енергії хаотичного руху молекул, потенціальної енергії взаємодії між ними і внутрішньомолекулярної енергії.

У термодинамічні формули входить не сама енергія, а її зміна, що пов’язана зі зміною деякого параметра. Тому внутрішню енергію можна визначати з точністю до довільної адитивної сталої, вибираючи її так, щоб вираз для енергії був простим. Так, зазвичай вивчаються процеси, при яких внутрішньомолекулярна енергія залишається постійною. Тому цю енергію у внутрішній енергії можна не враховувати.

Внутрішня енергія системи тіл складається із внутрішньої енергії кожного з окремих тіл й енергії взаємодії між тілами. Остання являє собою енергію взаємодії в тонкому шарі на границі між тілами. Вона є малою у порівнянні з енергією окремих макроскопічних тіл. Тому нею можна знехтувати й вважати, що внутрішня енергія системи макроскопічних тіл дорівнює сумі внутрішніх енергій цих окремих тіл. Отже, внутрішня енергія є величина адитивна.Внутрішня енергія є функцією стану системи. Це означає, що незалежно від попередньої історії системи її енергія в даному стані має визначені йому значення. Тому збільшення внутрішньої енергії при переході системи з одного стану в інший завжди дорівнює різниці значень внутрішньої енергії в кінцевому й початковому станах незалежно від шляху (процесу), за яким відбувався перехід системи з одного стану в інший. Теплоємністю тіланазивається величина, що дорівнює кількості теплоти, яку потрібно передати тілу, щоб підвищити його температуру на один градус Кельвіна. Тобто

,

де  – кількість теплоти, передача якої підвищує температуру тіла на  . Теплоємність тіла виміряється в джоулях на кельвін (Дж/К).

Питомою теплоємністю називають теплоємність одиниці маси речовини

,

де  – маса тіла. Виміряється вона в джоулях на кілограм-кельвін (Дж/(кг∙К)).

Молярною теплоємністю називають теплоємність моля речовини .

,

де  – кількість молів речовини тіла. Виміряється вона в джоулях на моль-кельвін (Дж/(моль∙К)).

Питома й молярна теплоємності пов'язані співвідношенням

25. Зміна внутрішньої енергії закритої системи, яка відбувається в рівноважному процесі переходу системи із стану 1 в стан 2, дорівнює сумі роботи, зробленої над системою зовнішніми силами, і кількості теплоти, наданої системі: ΔU = A' + Q. Робота здійснена системою над зовнішніми тілами в процесі 1->2 (Назвемо її просто А) A=-A', тоді закон приймає вигляд:

.

Кількість теплоти, що надається системі, витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

Для елементарної кількості теплоти δQ; елементарної роботи δA і малої зміни dU внутрішньої енергії перший закон термодинаміки має вигляд:

26. Адіаба́тний проце́с (грец. αδιαβατος — неперехідний) — в термодинаміці зміна стану тіла без обміну теплом з навколишнім середовищем. Його можна здійснити, проводячи стискання чи розширення тіла (наприклад, газу) дуже швидко.

Так, при поширенні звукових хвиль у повітрі чи іншому тілі, у місцях згущення частинок температура підвищується, а в місцях розрідження — знижується. За дуже малий період коливання не відбувається помітного обміну теплом між місцями згущення і розрідження.

Під час адіабатного стискування тіла внутрішня енергія його збільшується, а при адіабатичному розширенні — зменшується. Виконана робота при цьому дорівнює за величиною і протилежна за знаком зміні внутрішньої енергії системи.

де P — тиск, V — об'єм,   — показник адіабати,

 — молярна теплоємність за умов постійного тиску, а   — молярна теплоємність за умов постійного об'єму

28. Дру́гий закон термодина́міки — один із основних законів фізики, закон про неспадання ентропії в ізольованій системі. Він накладає обмеження на кількість корисної роботи, яку може здійснити тепловий двигун. На засадничому рівні другий закон термодинаміки визначає напрямок протікання процесів у фізичній системі - від порядку до безпорядку. Існує багато різних формулювань другого закону термодинаміки, загалом еквівалентних між собою.

Для системи із сталою температурою існує певна функція стану S — ентропія, яка визначається таким чином, що

1. Адіабатичний перехід із рівноважного стану A в рівноважний стан B можливий лише тоді, коли

.

2. Приріст ентропії у квазістаціонарному процесі дорівнює

,

де T — температура.

29. Електричний заряд – це невіддільна властивість деяких елементарних частинок.

До елементарних частинок відносяться такі мікрочастинки, для яких сучасними засобами фізики не можна доказати, що вони є об’єднаннями інших мікрочастинок.

Відомо, що заряди бувають двох видів – позитивні й негативні. Носієм елементарного негативного заряду є електрон. Елементарним позитивним зарядом наділений протон.

За абсолютною величиною елементарні заряди електрона й протона однакові. За одиницю електричного заряду прийнято кулон (Кл).

Точковим джерелом заряду називається заряджене тіло, форма й розміри якого в даних умовах не є суттєвими.

 

Дослідним способом було доказано, що сила взаємодії двох нерухомих точкових зарядів пропорційна величині кожного із зарядів і обернено пропорційна квадрату відстані між ними.

Закон взаємодії точкових зарядів називається законом Кулона

 

де q₁ і q₂ - точкові електричні заряди;  - діелектрична стала; r – відстань між точковими зарядами.

27. Коловим процесом (циклом) називається процес, при якому система, пройшовши через ряд станів, повертається у вихідний стан. На діаграмі процесів цикл зображається замкненою кривою.

Тіло, яке здійснює коловий процес і обмінюється енергією з іншими тілами, називається робочим тілом. Звичайно таким тілом є газ.

Цикл, який виконує ідеальний газ, можна розбити на процеси розширення   і стискання   газу (рис.30). Робота розширення, яка визначається площею фігури  , додатна  , робота стискування, що визначається площею фігури  , від'ємна  . Робота, яка виконується газом за цикл:

.

Рис.30.           Ця робота визначається заштрихованою площею, що охоплюється кривою   .

 

 

Якщо за цикл виконується додатна робота   (цикл виконується за годинниковою стрілкою), то він називається прямим.

Тепловий двигун характеризується коефіцієнтом корисної дії  , який дорівнює відношенню роботи  , яка виконана тілом за цикл роботи, до кількості теплоти  , що отримало тіло від нагрівника:

.

Теорема Карно: із всіх періодично діючих теплових машин, що мають однакові температури нагрівачів і холодильників, найбільший К.К.Д. мають оборотні машини; при цьому К.К.Д. оборотних машин, що працюють при однакових температурах нагрівачів і холодильників, дорівнюють один одному і не залежать від конструкції машини.

Цикл Карно складається з двох ізотерм і двох адіабат (рис.34).        

  Рис.34

 

Ізотермічне розширення і стиск задані відповідно кривими   і  , адіабатне розширення і стиск - кривими   і  . Для виконання циклу Карнонеобхідні термостат з температурою   (нагрівник) і термостат з температурою   (холодильник), причому  . При проходженні адіабатних ділянок циклусистема повинна бути термоізольованою від навколишнього середовища.

Визначимо К.К.Д. циклу Карно. При ізотермічному процесі   і робота розширення газу   дорівнює кількості теплоти  , що отримав газ від нагрівника:

.

При адіабатному розширенні робота виконується за рахунок зміни внутрішньої енергії:

.

21.Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.

Матеріальна точка, що довільно рухається у просторі, має три ступені вільності  . Якщо ця точка рухається по деякій поверхні або вздовж певної кривої,то вона відповідно має два або один ступені вільності.

Абсолютно тверде тіло має 6 ступенів вільності. Щоб визначити його положення в просторі, треба задати три координати   (3 ступені вільності поступального руху) центра мас тіла (рис.8); два кути   і  , які визначають положення в просторі певної осі  , яка проходить через центр мас і яку-небудь іншу фіксовану точку тіла і необхідно задати кут  , який визначає напрямок другої зв’язаної з тілом осі, яка перпендикулярна до першої (  - 3 ступені вільності обертального руху).

Рис.8

 

Якщо тіло не абсолютно тверде і його частини можуть зміщуватись одна відносно одної, то необхідно ввести ще додаткові ступені вільності коливального руху.

Молекули одноатомного газу можна розглядати як матеріальні точки на тій підставі, що маса такої частинки зосереджена в ядрі, розміри якого дуже малі. Молекула одноатомного газу має три ступені вільності поступального руху (рис.9).

 

Рис.9

 

Її середня кінетична енергія   дорівнює кінетичній енергії молекули, що рухається з швидкістю, яка дорівнює середній квадратичній швидкості  :

.

Враховуючи, що  , маємо:

.

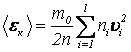Середня кінетична енергія, що припадає на один ступінь вільності (с.в.) молекули, на рух вздовж осі   дорівнює:

,

тому що рух вздовж цієї осі відбувається тільки за рахунок складової   вектора   швидкості  -тої молекули газу. Внаслідок хаотичності теплового руху молекул ідеального газу:

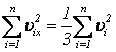, тому  .

У класичній статистичній фізиці виводиться закон Больцмана про рівномірний розподіл енергій за ступенями вільності молекул: для статичної системи, що перебуває у стані термодинамічної рівноваги, на кожний поступальний і обертальний ступінь вільності припадає в середньому кінетична енергія, що дорівнює  , а на кожний коливний ступінь вільності - в середньому енергія  .

Коливний ступінь має вдвічі більшу енергію тому, що на нього припадає не лише кінетична енергія (як у разі поступального і обертального руху), але і потенціальна енергія, причому середні значення кінетичної і потенціальної енергій однакові:

.

Таким чином, середня енергія молекули:

,

де   - кількість ступенів вільності молекули.

30. Напряженность и потенциал электрического поля и связь между ними.

Напряженность это силовая характеристика, а Потенциал это энергетическая характеристика. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал   , на близко расположенную эквипотенциальную поверхность, имеющую потенциал  Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения  С другой стороны   . Из этих уравнений получаем

Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

31. Электрическая емкость. Конденсаторы.

Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд, измеряется в фарадах.

где   — заряд,   — потенциал проводника.

Конденса́тор  двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля

32. Электрический ток. Сила и плотность тока.

Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц

Сила тока — физическая величина  , равная отношению количества заряда  , прошедшего через некоторую поверхность за время  , к величине этого промежутка времени^[1]:

измеряется в амперах

По закону Ома сила тока   для участка цепи прямо пропорциональна приложенному напряжению   к участку цепи и обратно пропорциональна сопротивлению  проводника этого участка цепи:

По закону Ома сила тока   для участка цепи прямо пропорциональна приложенному напряжению   к участку цепи и обратно пропорциональна сопротивлению  проводника этого участка цепи:

Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичной площади^[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:

где I — сила тока через поперечное сечение проводника площадью S

33.Электро движущая сила. Закон Ома.

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил  , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре   ЭДС будет равна:

где   — элемент контура.

Закон Ома для полной цепи:

где:

 — ЭДС источника напряжения,

 — сила тока в цепи,

 — сопротивление всех внешних элементов цепи,

 — внутреннее сопротивление источника напряжения.

Закон Ома для участка цепи: