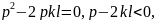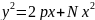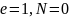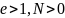Парабола.

Параболаның жабайы теңдеуі. Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын нүктелердің геометриялық орындарын парабола дейміз.

Параболаның жабайы теңдеуін қорытып шығару үшін жоғарғы анықтамаға сәйкес сызба сызайық

54-сызба

Берілген F нүктесінің координаталары былайша белгіленеді: (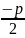 ,0) . Бұл нүкте параболаның фокусы деп аталады. Координаталардың бас нүктесінен қашықтықтағы әрі ордината осіне параллель берілген (D) түзуін параболаның директрисасы дейміз. Параболаның бойындағы кез келген нүктені M(x, y) дейік.

Анықтама бойынша:

FM=ME (1)

Екі нүктенің ара қашықтығының формуласы бойынша:

FM=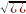 +x=CO+ON.

Осы қашықтықтардық мәндерін (1) теңдігіне қойып , параболаның жабайы теңдеуін табамыз:

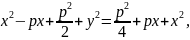
Мұндағы p- берілген фокус пен деректрисаның арасындағы қашықтық, параболаның параметрі; х пен у-параболаның бойындағы кез келген нүктенің ағымдық координаталары.

ME=R параболаның радиус- векторы деп аталады. Оның теңдігінің мынаған тең екенін көреміз:

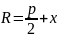
Парболаның дириктрисасы 54-сызбадан анықталады:

Параболаның эксцентриситетті:

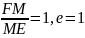
Мысал. Параболаның 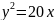теңдеуі бойынша оның фокусының директрисаға дейінгі қашықтығын және радиус- вектордың теңдеуін табайық.

Шешуі. Параболаның теңдеуі Осыдан 2p=20, p=10.

Бұл –фокустың директрисаға дейінгі қашықтығы. Радиус- вектор:

Параболанның түрін оның жабайы бойынша зерттеу .

55-сызба

Параболаның түрін зерттеу үшін оның жабайы теңдеуін у арқылы шешейік; у=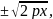 мұндағы p , х пен у – айнымалы шамалар. х-ке әр түрлі мән беріп, соған сәйкес у- тің мәндерін табамыз. Осыдан параболанның бойында жататын нүктелерді белгілеп, параболаның координаталар системасында қалай орналасатындығын қарастырайық.

1. Егер х=0, онда у=0. Демек , парабола координаталардың бас нүктесіннен өттеді.

2. Егер х , онда у= жорамал сан. Сондықтан ордината осінің сол жағында параболаның нақты нүктесі болмайды.

3. Егер х , онда у-тің осыған сәйкес нақты мәндері болады. х өскен сайын у-тің абсолют мәні де өсіп отырады. -тің әр бір мәніне у-тің әр қашанда екі мәні сәйкес келеді, яғни параболанің абсцисса осіне қарағанда симметриялы екі нүктесі болады.Бұл зерртеулерден мынадай қорытынды шығады: парабола – координаталардың бас нүктесінен өтіп, абсцисса осіне симметриялы, шексізге дейін өсе беретін қисық сызық (55-сызба).

Параболаның анықтамасы бойынша: FO=OC , F =

3.Параболаға жүргізілген жанама мен нормальдің теңдеулері. Параболаның теңдеуі және оның бойында жатқан нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін табайық. Параболаның =2px жабайы теңдеуі және (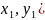 нүктесі берілген. Осы нүктеден жанама, нормаль және бір көмекші қиюшы түзу жүргізейік 57-cызба).

57-сызба

Қиюшы түзудің теңдеуі у- =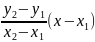 болады. және нүктелері параболаның бойында жатқандықтан, олардың координаталары параболаның теңдеуін қанағаттандырады. Сондықтан бұл екі нүктені координаталарын параболаның теңдеуіне қойып, оны түрлендірейік: 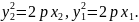Бірінші теңдеуден екінші теңдеуді алсақ

( ,

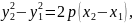
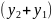Енді нүктесі нүктеге ұмтылса, онда болады. Бұл жағдайда қиюшы (Қ) түзуі (Ж) жанамасына айналады. Сондықтан

Осыдан

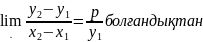
Бұл- параболаға жүргізілген жанаманың тедеуі.

Екі түзудің перпендикулярлық шарты бойынша нормальдық теңдеуі мынадай болады:

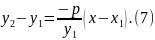
(6) теңдеуді қолайлы түрге келтірейік:

у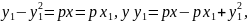

у яғни

у . (6’)

4. Параболаның диаметрлері. Анықтама. Берілген ба-ғытқа параллель хордалардың ортасындағы нүктелердің геомет-риялық орындарын параболаның осы бағытқа түйіндес диаметрі дейміз (58-сызба).

58-сызба

Параболаның у² = 2рх теңдеуі және осы параболаны қиып өте-тін А₁ В₁ хордасының у=һх +l теңдеуі берілген.

А₁ В₁ хордасының А₁ және В₁ нүктелері параболаның бойында жатқандықтан, бұл екі теңдеуден осы нүктелердің координаталарын табамыз:

у² = 2рх, у=һх +l, осыдан ,

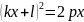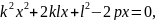
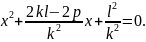
Осы квадрат теңдеуден Виет теоремасы бойынша:

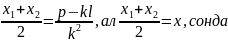
Виет теоремасы боиынша

Сонымен, хорданың ортасындағы нүктесінің координаталары:

А₁ В₁ хордасының ортасындағы С нүктесінің координаталары C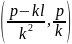 болады. Әрбір параллель хорданың l бос мүшесі әр түрлі болғандықтан, х-тің мәні әрбір хорданың ортасындағы нүкте үшін, мысалы С₁, С₂ нүктелері үшін (58-сызба), әр түрлі болады.

Ал хорданың ортасындағы нүктенің ординатасы параболаның параметрі мен хорданың теңдеуінің бұрыштық коэффициентіне тәуелді. Ендеше бұл ордината — барлық параллель хордалардың ортасындағы нүктелер үшін тұрақты шама. Сондықтан берілген к бағытына сәйкес параболаның диаметрі мынадай болады:

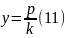
Бұл теңдеуден мынадай қорытындыға келеміз: параболаның диаметрі абсцисса осіне параллель болады. Демек, параболаның барлық диаметрлері абсцисса осіне параллель болу керек. к коэффициентінің мәніне сәйкес абсцисса осіне параллель әр түрлі диаметрлер болуы мүмкін. Егер к= 1 болса, онда диаметр у=р бола-ды. Егер к=∞ , онда диаметр у=0 болады. Соңғы жағдайда абсцисса осі параболаның диаметрі болады. Бұл параболаның бас диаметрі деп аталады (у = 0).

Эллипстің немесе гиперболаның барлық диаметрлері берілген нүктеде қиылысады. Осы диаметрлердің қиылысқан нүктесі эллипстің немесе гиперболаның центрі болады. Осыған байланысты эллипс пен гиперболаны центрлік қисықтар дейміз. Ал диаметрлері өз ара параллель болғандықтан, параболаны центрсіз қисық дейміз. Басқаша айтқанда, параллель диаметрлер шексізде қиылысады, сондықтан параболаның центрі шексізде болады.

5. Параболаның түзумен қиылысуы. Параболаның у² = 2рх теңдеуі мен түзудің у = bх+l теңдеуі берілген.

Егер түзу параболаны қиып өтсе, онда парабола мен түзудің қиылысқан нүктелерінің координаталары осы екі теңдеуді қанағаттандырады. Сондықтан бұл екі теңдеуді біріктіріп шығарайық:

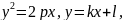
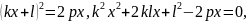
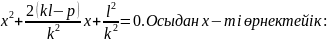
Мұндағы дискриминанттың мәніне байланысты үш түрлі жағдай болуы мүмкін:

1. 

2. 

3. 

р>0 оң таңбалы сан.

Бірінші жағдайда түзу параболаны екі нүктеден қияды. Мұндағы х-тің нақты екі мәніне у-тің нақты екі мәні сәйкес келеді.

Екінші жағдайда түзу парабодаға жанама болады, яғни түзу мен парабола бір нүктеде қиылысады. Түзудің параболаға жанама болу шарты: р — 2kl = 0, осыдан

р = 2kl. (13)

Бұл жағдайдағы жанасу нүктесінің координаталары: M .

Үшінші жагдаида түзу параболаға қиюшы да және жанама да болмайды, яғни түзу параболаның сыртынан өтеді. Сонда (12) теңдеудегі х-тің мәндері жорымал сан болады. Екінші жағдайдағы жанасу нүктесінің координаталары тіпті оңай табылады: (12) теңдіктен

Енді M нүктесінің координаталары оңайланды:

M .

Сонымен, түзу параболаға жанама , болса, онда:

Осы (13) шарт орындалғанда жанама, парабола жане оның

диаметрі бір нүктесінде қиылысады.

6. Эллипс, гипербола және параболаның графиктерін анықтамалары бойынша салу. Эллипс, гипербола және параболаның графиктерін анықтамалары бойынша салайық.

1. Эллипстің екі Ғ₁, Ғ₂ фокусы және 2а үлкен осі берілген. Оның графигін салайық.

Эллипстің графигін құру үшін оның анықтамасын пайдаланайық. Берілген Ғ₁, Ғ₂ фокустар-ды және 2а үлкен осьті тік бұрышты координаталар системасына өлшеп салайық (60-сызба). Ғ₁Ғ₂ = 2с кесіндінің ортасын табайық: Ғ₁О = Ғ₂О немесе N₁O=ON₂. О нүктесінен М₁М₂ кесіндісін жүргізейік. N ₁O = а радиусымен Ғ₁ фокусынан доғашықтар жүргізіп, М₁ және М₂ нүктелерін табайық: ОМ₁ = ОМ₂ = b. Ғ₁ және О нүктелердің арасынан өз еркімізше бірнеше нүкте алайық: А, В, С, О,... Енді N₁A, N₂А радиустарымен Ғ₁ және Ғ₂ фокустарынан доғашықтар жүргізіп, эллипстің 4 нүктесін табамыз. Өйткені N₁A + N₂А = 2а. Сол сияқты N₁B, N₂В радиустары мен Ғ₁ Ғ₂—фокустарынан доғашықтар жүргізіп, тағы да эллипстің 4 нүктесін (С_1, С₂, С₃, С₄) табамыз. Осы нүктелерді коссақ, эллипстің графигі шығады (60-сызба).

2. Гиперболаныц фокустары және нақты осі берілген. Оның графигін салайық.

Кесінді арқылы берілген 2а мен 2с-ні тік бүрышты координаталар осьтерінің бойына өлшеп салайық. Онан кейін Ғ₁Ғ₂=2с кесіндінің ортасындағы нүктені табайық: Ғ₁О = = Ғ₂О немесе N₁О =О N₂=а. Ғ фокусының сол жағынан еркімізше бірнеше А, В, С, D, ... нүктелерін алайық (61-сызба).

60-сызба

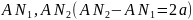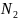радиустарымен екі фокустан доғашықтар жүргізіп, гиперболаның 4 нүктесін табамыз. B , B (В — =2а) радиустарымен екі фокустан тағы да доғашықтар жүргізіп, гиперболаның нүктелерін анықтаймыз. Осы нүктелерді қоссақ, гпперболаның графигі шығады (61-сызба).

61-сызба

3. Параболаның Ғ фокусы мен ( ) директрисасы берілген. Оның графигін салайық.

62-сызба

Параболанын анықтамасы бойынша, оның нүктелерін табу үшін ең әуелі фокус пен директрисаның ортасындағы нүктені аныктайық: АВ = ВҒ (62-сызба). В нүктесі параболаның төбесі. Енді В нүктесінің оң жағынан өз еркімізше бірнеше С, М, Е, D... нүктелерін алып, сол нүктелерден директрисаға параллель түзулер жүргізейік (62-сызба). АС радиусымен Ғ фокусынан доғашықтар жүргізейік. Сол сиякты МА, ЕА радиустарымен фокустан тағы да доғашықтар жүргізіп, параболаның нүктелерін табамыз. Осыдан шыққан нүктелерді қоссақ, параболаның графигі шығады.

^{1.Тік бұрыш координаталар системасындағы екінші ретті қисықтарды төбелері сәйкес келетін тедеңдеу. Эллипс, гипербола және параболанның әрқайсысының жабайы формулаларын жеке-жеке қорытып шығардық. Енді координаталар системасындағы осы үш қисықтың теңдеуін қанағаттандыраттын бір жалпы теңдеуді қорыттып шығарайық.}

Ең әуелі эллипстің 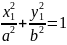теңдеуін қарастырайық. Бұл- центрі координаталардың осьтері координаталар осьтерінің бойында жатқан эллипстің теңдеуі (63-сызба).

^{63-сызба}

^{Енді координаталар системасының бас нүктесін эллипстің сол жағындағы төбесіне орнатайық, басқаша айтқанда координаталар системасын ордината осіне паралель жылжытып, оның бас нүктесін эллипстің сол жағындағы төбесіне көшірейік. Ескі координаталар системасы} ал жаңа координаталар системасы хОу болсын (63-сызба). Координаталар системасының түрлендіру формуласы бойынша:

Осы мен 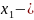дің мәндерін теңдеуіне қойып, оны түрлендірейік:

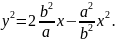
Мұндағы p=

Осы мәндерді алдыңғы теңдікке қойып, эллипстыің сол төбесіне сәйкес келетін теңдеуді табайық:

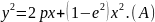
Енді 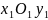координаталар системасына сәйкес келетін гиперболаның жабайы теңдеуін қарастырайық.

Жаңа координаталар системасы хОу болсын. Осьтердің бағыттарын өзгертпей, координаталардың бас нүктесін гиперболанның оң төбесіне көшірсек, онда түрлендіру формуласы бойынша

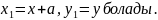
Ескі координаталардың орнына жаңа кллрдинаталарды қойып, гиперболанның оң жақ төбесіне сәйкес келетін теңдеуін табайық:

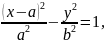
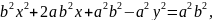
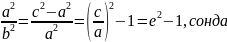
Сонымен, (А) және (В) тецдеулері бірдей болып шыкты.

Төбесіне сәйкес келетін параболаныц жабайы теңдеуі бізге белгілі у² = 2рх. Енді осы екі теңдеуді (А, В) салыстырсақ, бұлардың бір-бірінен айырмасы эксцентриситетке байланысты, яғни е<1 эллипс, е> 1 гипербола, е=1 парабола болады.

е= 1 болғанда (В) тендеуі у² = 2рх теңдеуіне айналады.

Сөйтіп, үш қисықтың төбелеріне сәйкес келетін жалпы теңдеуі мынадай болады:

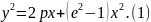
Бұл тендеуге сәйкес келетін үш қисықтың координаталар системасында қалай орналасатынын 64-сызбадан көруге болады. Мұнда үш қисықтың жалпы төбесі О нүктесінде жатыр. Осы үшеуіне ортақ жаңа координаталар системасы хОу. Бұл түрлендірудегі р параметрінің таңбасы оң (р>0) болады.

Егер түрлендіру эллипс үшін

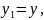
ал гипербола үшін

болса, онда р параметрі теріс таңбалы (p<0) болады. Бұл жағдайдағы график 65-сызбада көрсетілген.

64-сызба

Егер е²- 1=N десек, онда (1) теңдеу былайша жазылады:

мұндағы N теңдеудің параметрі деп аталады.

Егер N<0 болса, онда теңдеу эллипстікі. Егер N=0 болса, тецдеу

мұндағы N теңдеудің параметрі деп аталады.

Егер N<0 болса, онда теңдеу эллипстікі. Егер N=0 болса, теңдеу

параболанікі.

65-сызба

Егер N>0 болса, онда тендеу гиперболанікі. Эксцентриситеттің (е) немесе параметрдің (N) мәніне байланысты шығатын үш түрлі жағдай 2-таблицада көрсетілген.

N=
Қисық	Эллипс	Парабола	Гипербола

2. Эллипс, гипербола және параболаның жалпы полярлық теңдеуі. Бүл параграфта эллипс, гипербола және параболаның жалпы полярлық теңдеуін қарастырайық.

1) Эллипстің полярлық теңдеуін шығару үшін фокусты по­люс деп, ал М нүктесінің полярлық координаталарын ρ және φ деп алайық (66-сызба).

тік бұрышты үшбүрышынан , осыдан

Эллипстің радиус-векторының формуласы бойынша

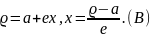
(А) және (В) теңдіктерін теңестіріп, эллипстің сол жағындағы фокусқа сәйкес келетін полярлық тендеуін табайық:

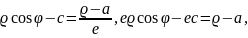
66-сызба

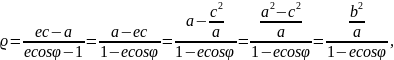
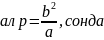
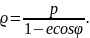
2) Гиперболаның полярлык, теңдеуін шығару үшін оның оң жағындағы фокусын полярлық полюс деп, ал гиперболаның бойындағы М нүктесінің координаталарын тағы да ϱ және φ деп алайық (67-сызба).

67-сызба

тік бұрышты үшбұрышынан

Гиперболаның радиус-векторының формуласы бойынша

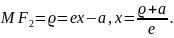
Соңғы екі теңдіктегі x-тің мәндерін теңестіріп, гиперболаның оң фокусына сәйкес келетін полярлық теңдеуін табайық:

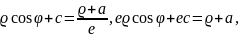
67-сызбадағы 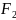фокусы по­люс, φ бүрышы амплитуда, ал радиус-вектор болады.

3) Параболаның полярлық теңдеуін шығару үшін оның жалғыз фокусын полярлык полюс деп, ал параболаның бойында жатқан М нүктесінің координаталарын ϱ және деп белгілейік (68-сызба).

68-сызба

МҒD тік бүрышты үшбүрышынан:

Параболаның анықтамасы бойынша , осыдан

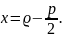
Соңғы екі теңдеудегі х-тің мәндерін теңестіріп, параболаның полярлык, теңдеуін табайық:

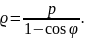
Сөйтіп, эллипс, гипербола, параболаның жалпы полярлык теңдеуі мынандай болады:

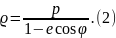
Егер е<1 болса, бұл теңдеу эллипстікі. Егер е>1 болса, онда бұл теңдеу гиперболанікі. Егер е= 1 болса, онда теңдеу параболанікі. Ал амплитуда, ол 0-ден 2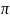 -ге дейін өзгереді.

Осы екі параграфтағы эллипс, гипербола және параболанын (1) және (2) теңдеуінің шығуы сол үш қисықтың жалпы қасиетіне негізделген. Яғни берілген фокустан қисықтың бойында жатқан нүктеге дейінгі қашықтықтың сол нүктеден осы қисықтарға сәйкес келетін директрисаға дейінгі қашықтыққа қатынасы (66, 67, 68-сызбалар) эксцентриситет деп аталатын түрақты шамаға тең:

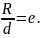
Егер эллипс, гипербола және параболадағы поляр координата­лар системасының бағытын өзгертпей, олардың полюсін басқа фокустарға сәйкес алсақ, онда (2) формула мынадай түрде жазылады:

Бүл жағдайда парабола полярлық осьтің сол жағына қарай бағытталады.

3. Екінші ретті қисықтың теориясына қосымша мәселелер. Аполлоний теоремалары. 1. Эллипстің екі түйіндес диаметрі квад-раттарынын қосындысы оның екі осьтері квадраттарының қосын-дысына тең, яғни (69-сызба):

69-сызба

Дәлелдеме. 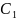С₂ диаметрінің теңдеуі у=кх болсын. Осы диаметрдің эллипспен киылысатын нүктелерінің ко­ординаталарын табайык. Ол 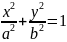және у=kx тендеулерін біріктіріп шешейік:

b²х² + а²к²х² = а²b². Осыдап х-тің мәнін, сонан кейін у-тің

мәнін табамыз:

Ал нүктелерін координаталары арқылы жазайық:

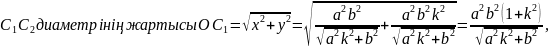
Енді эллипстің С₂ диаметріне түйіндес 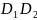диаметрімен ки­ылысатын нүктелердің координаталарын іздейік. Ол үшін диаметршің 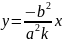теңдеуі мен эллипстін теңдеуін біріктіріп шығарайық:

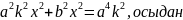
Бұл нүктелерінің координаталары. диаметрінін жартысы

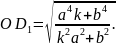
Жоғарыда шығарылған екі түйіндес жарты диаметр тендеулерінің екі жағын квадраттап қосайық, яғни

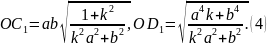
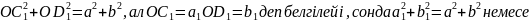
Осымен дәлелденді.

2. Эллипстің екі түйіндес диаметрлерінен құрылған параллелограмның ауданы оның екі осьтерінен күрылған тік бұрышты төртбұрыштың ауданына тең (69-сызба), яғни

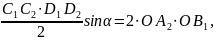
мүндағы α екі түйіндес диаметрдің арасындағы бұрыш.

Дәлелдеме. Екі 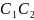және түйіндес диаметрлерінің арасындағы бұрышты анықтайық. Бұл түйіндес диаметрлердің теңдеулері мынадай:

Екі түзудің арасындағы бұрышты анықтайтын формула бой­ынша:

Осыдан 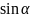табайық:

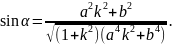
Түбірдің таңбасы плюс, өйткені а< 180°.

Енді жоғарыдағы 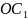және дің мәндерін (4) пайдаланайық:

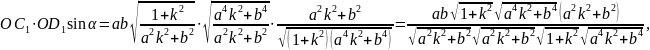
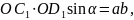
Немесе

Ал

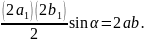
Немесе

Осымен дәлелденді.

70-сызба

3. Гиперболаның екі түйіндес диаметрі квадраттарыныц айырымы онын екі осьтері квадраттарының айырымына тең (70-сызба), яғни

Немесе

Дәлелдеме. диаметрінің гиперболамен қиылысатын нүктелерінің координаталарын табайық. Ол үшін гиперболанын теңдеуі мен диамстрініц у = kх теңдеуін біріктіріп шешейік:

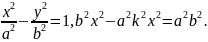
Осыдан

Мұндағы 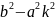>0 деп ұйғарамыз. Сонда

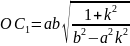
диаметріне түйіндес диаметрі гиперболаны емес (70-сызба), осы гипсрболага түйіндес гиперболаны

қияды. Сондықтан диаметрінің у= 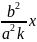теңдеуін берілген

гиперболаға түйіндес гиперболаның теңдеуімен біріктіріп шығарып, және нүктелерінің координаталарын табайық:

Бұл — мсп нүктелерінің координаталары. Ал диаметрінің жартысы

Енді мына eкі теңдіктің

екі жағын квадраттап, бірінен екіншісін алсақ, онда іздеген формуламыз шығады, яғни

Ал

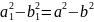
Немесе

4. Гиперболаның екі түйіндес диаметрінен кұрылған параллелограмның ауданы оның екі осьтерінен кұрылған тік бұрышты төртбұрыштың ауданына тең:

Дәлелдеме. Екі түйіндес диаметрдің арасындағы бұрышты олардың теңдеулері арқылы табайық:

Мұнан табамыз:

Енді жоғарыдағы 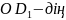мәндерін пайдаланайық:

немесе

Сонымен, мынадай төрт формула шықты:

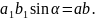
Бұл формулаларды алғаш шығарған грек ғалымы Аполлоний Перский. Ол біздің эрамызға дейінгі III ғасырда өмір сүрген. Аполлонийдің негізгі еңбегі «Конустык кималар» деп аталады. Конустық қималарды зерттеп, оның негізгі теориясын жасаған да Аполлоний болды.