Кіріспе

Геометрия (гр.geometrіa, ge — Жер және metrio — өлшеймін) — математиканың кеңістіктік пішіндер (формалар) мен қатынастарды, сондай-ақ, оларға ұқсас басқа да пішіндер мен қатынастарды зерттейтін саласы. Фигуралар кеңістіктік пішіндер болып есептеледі. Ал Аналитикалық геометрия – геометрияның қарапайым геометрия бейнелерді (түзулер, жазықтықтар, қисықтар, екінші реттік беттер) координаттар әдістерінің негізінде алгебралық амалдар арқылы зерттейтін бөлімі. Түзулерден кейін қисықтар ұғымы пайда болған. Сосын олардың түрлі қасиеттері зерттелген. Сол қисықтардың түрліше қасиеттеріне байланысты әр түрлі атауларға ие болады.

Жоғарыда айтылып кеткен жайттар біздің санамызда келесі сұрақтардың пайда болуына әсерін тигізеді:

Қисық ұғымы қалай және қандай себептерге байланысты пайда болды? Жалпы қисықтың қандай түрлері бар? Олар қандай қасиеттерге ие және олар қандай салада қолданыс табады? Бұл сұрақтардың жауаптарына біз осы курстық жұмыста келтірілген дәлелдеулер мен анықтамалар көмегімен көз жеткіземіз.

Курстық жұмыcтың өзектілігі: Екінші ретті қисықтар .

Зерттеудің мақсаттары: Екінші ретті қисықтар тақырыбын толық ашу. Аналитикалық гиометрия пәнінде екінші ретті қисық сызықтардың теориясы қанда й орын алатынын ашып көрсетті. Үш қисықтың қандай болаттынын ашып және практикада қолдануын қарастыру.

Зерттеудің міндеттері: эллипс, парабола, гиперболаның анықтамасы бойынша зертеу, қисық сызықтың жабайы теңдеулерін тік бұрышты координаталар системасында қорытып, сонымен қатар осы қисықтарды және олардың қасиеттерін теңдеулері арқылы зерттейік.

Зерттеудің пәні: Аналитикалық геометрия

Курстық жұмыстың құрылымы: Курстық жұмыс кіріспеден, төрт бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен құралған. Кіріспеде курстық жұмыстың өзектілігі, мақсаты және оларды шешу жолдары көрсетілген. Бірінші тарауда эллипс, гиперболла, парабола анықтамалары, сызбалары зерттелді. Екіншіэллипс, гипербола және параболаның графиктерін анықтамалары бойынша салу және жалпы теңдеулері көрсетілген. Үшінші тарауында екінші ретті қисықтарды практикада қолдану жазылған. Соңғысы қорытынды және пайдаланылған әдебиеттер тізімі қарастырылған.

Эллипс

Эллипстің жабайы теңдеуі. Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын эллипс дейміз. Енді эллипстің жабайы теңдеуін қорытып шығарайық. Ол үшін анықтамаға сәйкес сызба сызайық (36- сызба) . Анықтама бойынша:

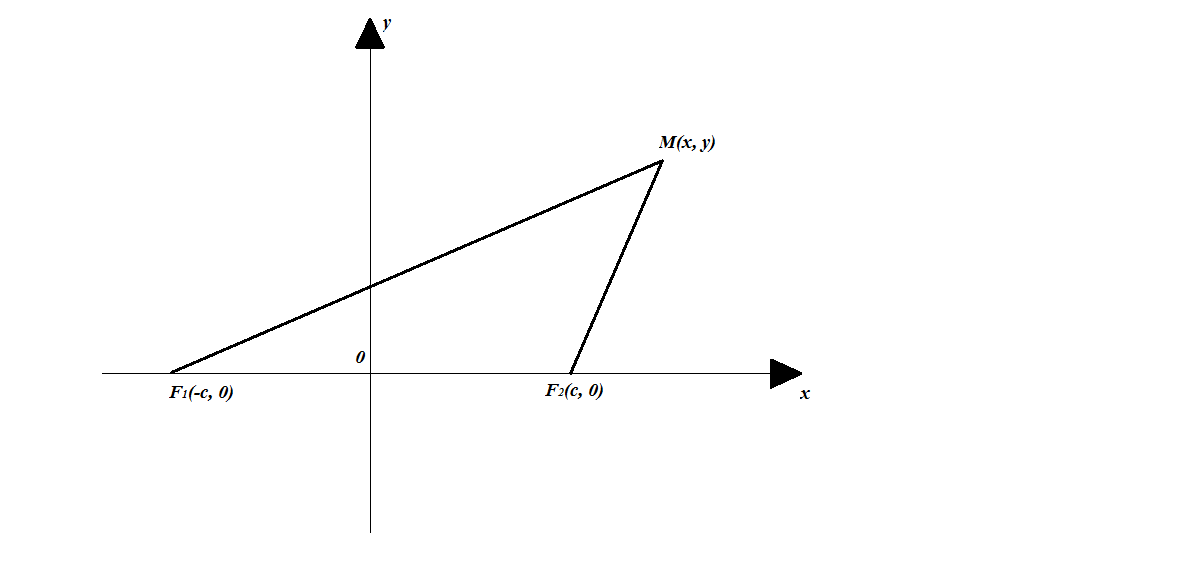36-сызба

Мұндағы фокус деп аталатын берілген нүктелер, М(х,у)-эллипстің бойындағы кез келген нүкте, – тұрақты шама.

Егер және Ғ₂ нүктелерінің ара қашыктығы Ғ₂ = 2с десек, онда осы екі нүктенің координаталары былай анықталады:

М және Ғ₂М қашықтықтарын

М,

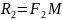
деп белгілесек, онда (1) теңдік мынадай түрде жазылады:

( )

Екі нүктенің ара қашықтықтығының формуласы бойынша:

.

Осы мәндерді ( ) теңдікке қояйық:

Бүл теңдікті түрлендіріп, эллипстің жабайы теңдеуін табайық:

,

+

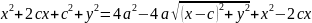a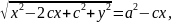

( )

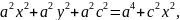
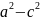егер а>с болса, а² — с²>0 болады, сондықтан

(2)

деп белгілейік, олай болса b²х² + а²у⁹ = а²b², осыдан

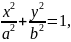(3)

мұндағы х пен у — эллипстің бойындағы кез келген нүктелердің координаталары, а — зллипстің үлкен жарты осі, b — оның кіші жарты осі. Бұл теңдеу эллипстің жабайы теңдеуі деп аталады. (3) теңдеудің дәрежесі жұп болғандықтан, эллипстің бойындағы М нүктесінің координаталары әрқашан да мынадай болады: М(±х, ±у). Сондықтан координаталар осьтері эллипске симметриялы, ал симметриалы осьтердің қиылысқан нүктесі эллипстің центрі болады.

Эллипстің түрін оның жабайы теңдеуі бойынша зерттеу.

Эллипстің жабайы теңдеуін у арқылы шешейік:

(3

мұндағы х пен у — айнымалы шамалар. x-тің мәндеріне сәйкес y-тің әр түрлі мәндері шығады. Енді (3') теңдеуін зерттейік.

_{1) Егер} х = 0 болса, онда 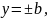яғни болады. Бұлар — ордината осінде жатқан эллипстің бойындағы нүктелер.

2) Егер х=±а болса, онда у = 0, яғни 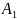(—а, 0), А₂(а, 0) бола-ды. Бұлар — абсцисса осінде жатқан эллипстің бойындағы нүктелер.

3) (3') теңдеуі х-тің барлық нақты мәндерінде қанағаттанады. Егер х-тің шамасы а-дан артық болса, онда у жорымал сан болады. Сондықтан эллипстің бойында жатқан нақты нүктелердің коорди-наталары а мен b-нің сәйкес шамаларынан артық болмау керек. Эллипстің барлық нүктелері қабырғалары 2а және 2b болатын тік төртбұрышпен шектелген, яғни —а х а және -b .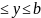

4) теңдігінен: а>b, а>с немесе 2a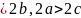 _. Мұндағы 2а — эллипстің үлкен осі, 2b — эллипстің кіші осі, 2с — эллипстің фокустарының ара қашықтығы.

Эллипстің жабайы теңдеуін зерттегеннен мынадай қорытынды шығады: эллипс координаталар системасында өзінің центріне симметриялы болып орналасатын тұйық қисық сызық (37-сызба) болады. Эллипстің центрі координаталар системасының центрінде жатады. 37-сызбадан: Ғ₂= 2c немесе = 2а.

Егер мен Ғ₂ нүктелерін қоссақ, онда О Ғ₂ тік бұрышты үшбұрыш шығады. Осыдан Пифагор теоремасы бойынша:

O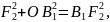

осыдан с² + b² = а². Бұл теңдік а, b, с шамаларының өз ара байланысын көрсетеді. 37-сызбадан және с² + b² = а² теңдігінен ОА₂=Ғ₂ екенін көреміз, яғни үлкен жарты ось әрқашан да фокустың нүктесінен ордината осінің бойындағы немесе В₂ нүктесіне дейінгі қашықтықа тең болады. А_1,В_1, А₂, В₂ нүктелері эллипстің төбелері деп аталады.

y

M(x, y)

x

0

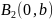
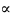
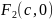
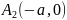
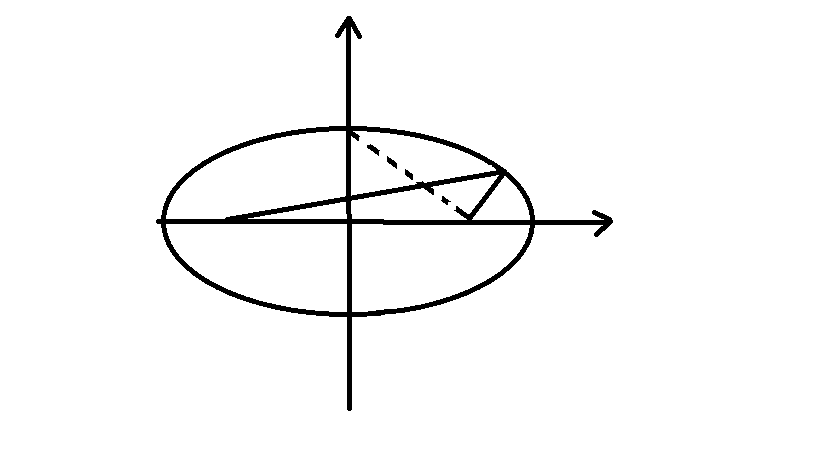37-сызба

Радиус-вектор және эксцентриситет. 1-параграфта эллипстің жабайы теңдеуін шығарумен байланысты мынадай теңдік шықты: . Бүл теңдіктің сол жағы +у²= сонда 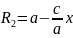. Анықтама бойынша

R₂-нің мәнін осы анықтамаға қойып, -ді табайық: = 2а-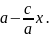 Сонымен, мынадай екі теңдік шықты:

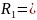- , (4)

мұндағы және эллипстің радиус-векторлары деп аталады. (4) теңдік — осы эллипстің радиус-векторларының формуласы.

қатынасы эллипстің эксцентриситеті деп аталады. Эксцентриситет е әрпімен белгіленеді.

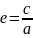. (5)

2-параграфтағы а² = b² + с² формуласынан а>с дегенбіз. Ендеше, эллипстің эксцентриситеті әрқашанда дұрыс бөлшек болады, яғни

е<1 немесе

Енді (4) теңдіктегі қатынасының орнына е-ні қойсақ, мынадай теңдіктер шығады:

- , (4´)

Егер МҒ₂ абсцисса осіне перпендикуляр болса (37-сызба), онда формуласындағы х = с болады. R₂=Р деп белгілесек, ондаp=a- яғни

мұндағы р фокальдық параметр деп аталады.

4.Шеңбер — эллипстің дербес жағдайы. Эллипстің жабайы

теңдеуі . Егер а = b болса, онда шеңбердің теңдеуі шығады: х²+у² = а². Бұл — центрі координаталардың бас нүктесінде жатқан, радиусы а-ға тең шеңбердің теңдеуі.

Алдыңғы параграфта а² = b² + с² теңдігі үш кесіндінің байланысын көрсетеді дегенбіз. Бұл жағдайда а=b болғаңдықтан, с=0. Ендеше шеңбердің эксцентритеті нольге тең, яғни 38-сызбада эллипстің жабайы теңдеуі мен шеңбердің х²+у² = а² теңдеуіне сәйкес келетін график керсетілген.

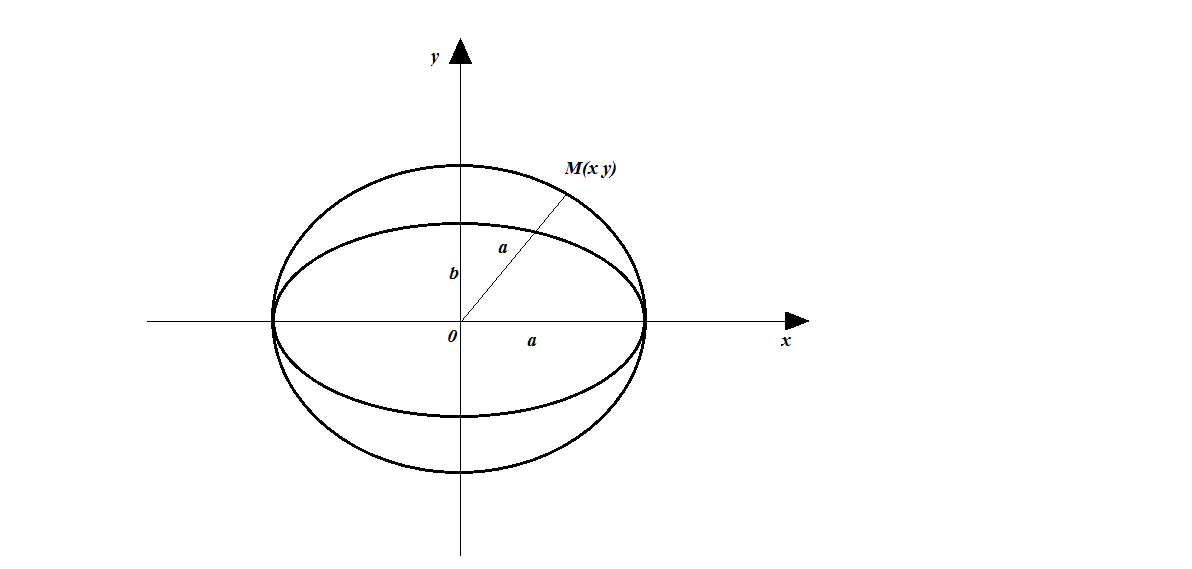
38- cызба

6. Эллипске жүргізілген жанама мен нормальдың теңдеулері.

Эллипстің теңдеуі және оның бойында жатқан бір нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін қорытып шығарайық.

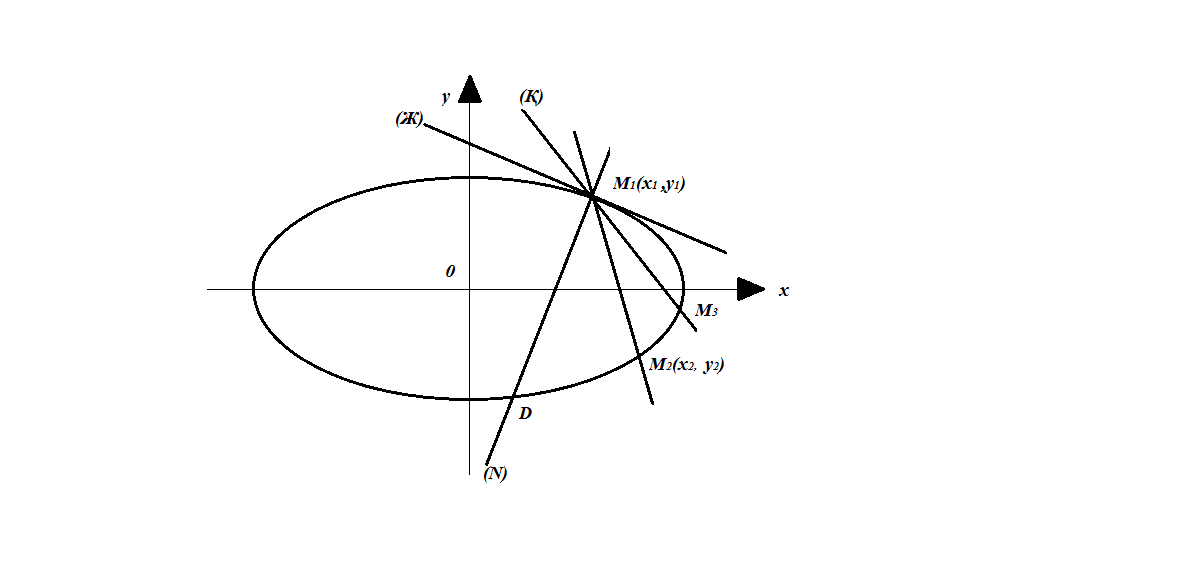
40-сызба

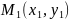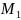1. теңдеуі, нүктесі берілген. Енді (Ж) жанамасы мен (N) нормалының теңдеулерін іздейік (40-сызба). нүктесінен қиюшы (Қ) түзуін жүргізейік. Берілген нүктесі қозғалмайтын, М₂ нүктесі қозғалатын нүктелер болсын. М₂ нүктесі берілген нүктесіне ұмтылғанда, қиюшы (Қ) түзуі жанамаға ұмтылады, яғни М₂ нүктесінің координаталары нүктесінің координаталарына тең болғанда = 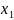, = 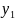яғни қиюшы түзу жанама болады. Қиюшы түзудің (екі нүктеден өтетін түзудің) теңдеуін жазайық:

Қиюшы түзудің және М₂ нүктелерінің координаталары эллипстің теңдеуін қанағаттандырады:

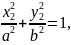
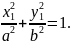
^Осы екі теңдіктің біріншісінен екіншісін алып тастап, қатынасын табайық:

М₂ нүктесі нүктесіне беттескенде limх₂ = , limу₂= болады. Сондықтан

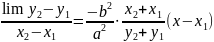
Қиюшы түзудің теңдеуіне (А) қатынасының мәнін қояйық:

М₂ нүктесі нүктесімен беттескенде қиюшы түзу жанама болады. Осыдан жанаманың теңдеуі шығады:

2. Берілген жанамаға перпендикуляр болатын түзуді нормаль деп атайды. 40-сызбада — жанамаға перпендикуляр. Ендеше, екі түзудің перпендикулярлық шарты 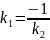бойынша нормальдың теңдеуі жазылады:

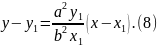
3. Жанаманың теңдеуін қолайлы түрге келтірейік. Ол үшін (7) теңдеуді түрлендірейік.

Осы теңдіктің оң жағындағы қосынды эллипстің жабайы формуласы бойынша бірге тең. Сонда іздеген жанаманың жабайы теңдеуі шығады:

4. Нормальдың теңдеуін екінші түрге келтірейік. Ол үшін (8) теңдеуді түрлендірейік:

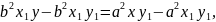
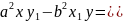
1-параграфтағы (2) формула бойынша: а² — b² = с², сонда

=

7. Эллипстің түйіндес диаметрлері. Эллипстің центрінен өтетін түзулерді эллипстің диаметрлері дейміз. Эллипстің екі нүктесінен өтетін түзуді эллипстің хордасы, ал центрден өтетін хорданы оның диаметрі дейміз. Сонымен, эллипске көптеген диаметрлер мен хордалар жүргізуге болады. Эллипстің осындай диаметрлерінің ішіндегі түйіндес екі диаметрін қарастырайық.

Аныцтама. Бір диаметрге параллель жүргізілген хордаларды екінші диаметр қақ бөлсе, онда осы екі диаметрді (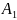 А₂ және В1В₂, 42-сызба) түйіндес диаметрлер дейміз. Бұл анықтама бойынша түйіндес диаметрлердің әрқайсысы параллель хордалардың орталарынан етегін нүктелердің геометриялық орындары болады. Мұнымен қатар әрбір түйіндес диаметрге параллель хордалар екінші диаметрге түйіндес болады.

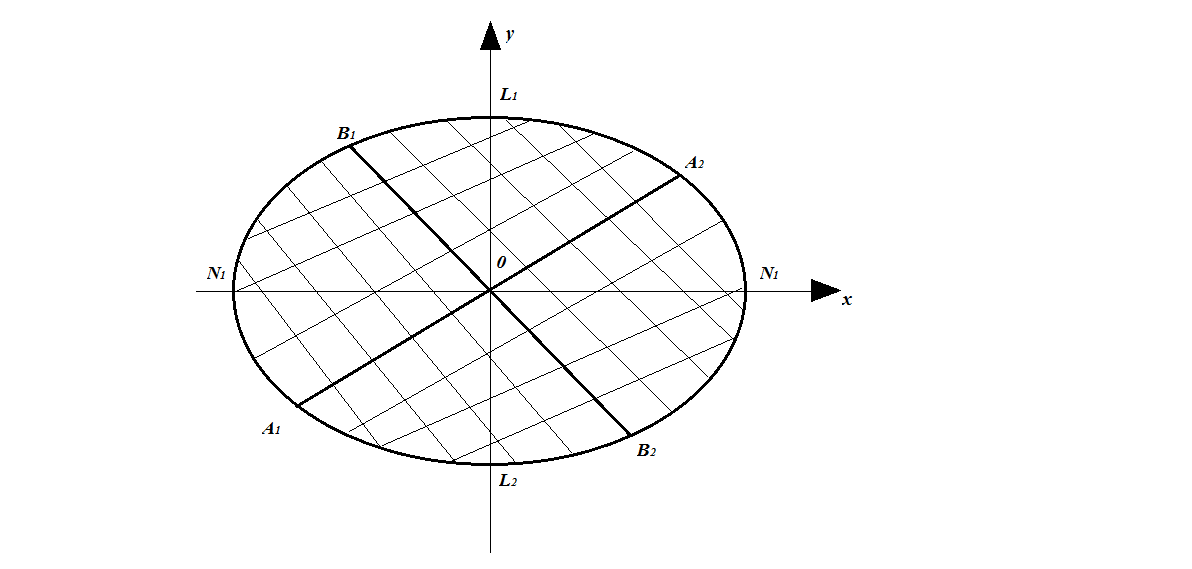42-сызба

42-сызбадағы А₁А₂ және В₁В₂ диаметрлері — түйіндес диаметрлер. Эллипстің және 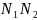осьтері де — өз ара (ортогональдық) түйіндес диаметрлер.

Эллипстің теңдеуі және эллипстің диаметріне түйіндес хорданың у = kх + l пең-деуі берілген. Осы хордаға түйіндес диаметрдің теңдеуін табайық.

Ол үшін түйіндес екі А₂, В₂ диаметрін жүргізіп, берілген хорда мен (х) түйіндес диаметрінің қиылысқан нүктесінен абсцисса осіне МО перпендикулярын (43-сызба) түсірейік.

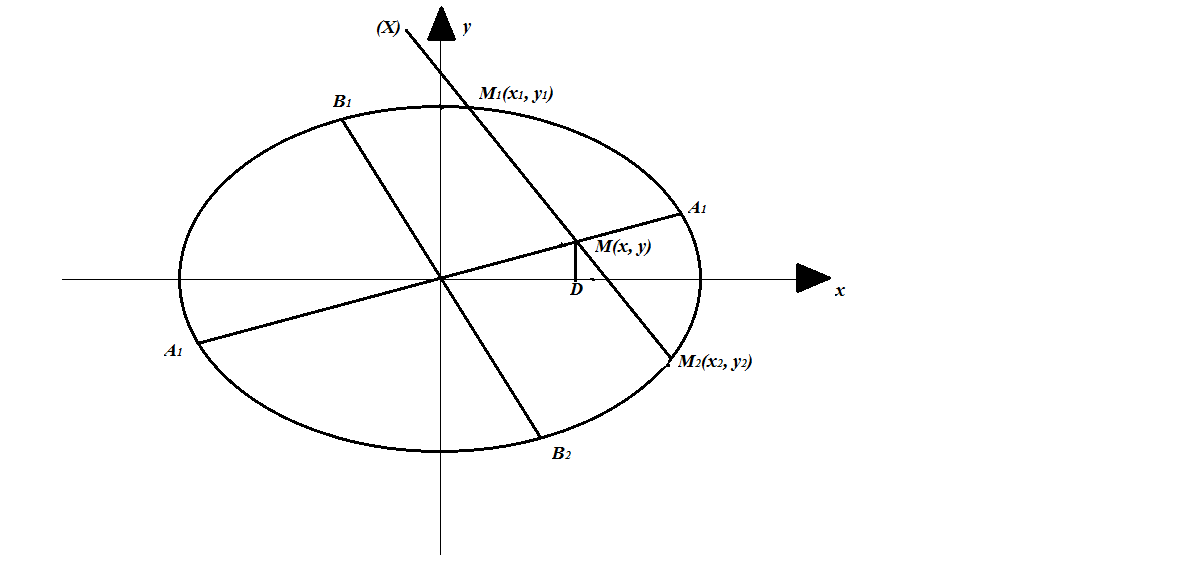43-сызба

Хорданың және М₂ ңүктелері эллипстің бойында жатқандықтан, эллипстің теңдеуі мен хорданың теңдеуін біріктіріп шешейік:

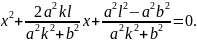
Бұл квадрат теңдеуден Виет теоремасы бойынша:

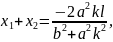
Енді осы сияқты мен у₂ қосындысының жартысын, яғни 43-сызбадағы М₁М₂ хордасының ортасындағы нүктенің координаталарын іздейік. Хорданың теңдеуінен Осыны эллипстің теңдеуіне қойсақ:

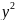( ) -2

Виет теоремасы бойынша:

М(х, у) нүктесі (43-сызба) хорданы дәл екіге бөледі. Сондықтан

яғни

Соңғы екі теңдіктен:

Демек, (13) теңдеу — берілген у = кх + l хордаға түйіндес диаметрдің теңдеуі.

Бұл теңдеуді қарастырғаннан мынадай қорытынды шығады:

1) эллипстің диаметрі координаталардың бас нүктесінен өтеді;

2) деп белгілесек, онда (13) теңдеу былайша жазылады:

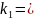
мұндағы хордаға түйіндес А₁А₂ диаметрінің бұрыштық коэффициенті. к және к_х бұрыштық коэффициенттерінің

кебейтіндісі к₁к = — тұрақты теріс шама. Ендеше, эллипстіц

түйіндес екі диаметрінің бұрыштық коэффициенттерінің таңбалары

қарама-қарсы болады, яғни бірінің таңбасы оң болса, екіншінің

таңбасы теріс болады. Ал түйіндес диаметрдің біреуі Ох осімен

сүйір бұрыш жасаса, екіншісі доғал бұрыш жасайды.

8. Эллипстің директрисалары. Эллипстің графигін салып, оның екі жағынан бірдей қашықтықта тұратын, ордината осіне параллель екі түзу жүргізейік (45-сызба). Бұл екі түзудің әрқайсысы ордината осінен d қашықтықта болсын. Радиус-вектор R₂ = МҒ₂=а—ех. 45-сызбадан d=ЕС, МС = ЕС-ЕМ = d-Od = d-х.

Сонымен, МС = d—х.

Енді радиус-вектордың эллипстің бойындағы нүктеден түзуге дейінгі қашықтыққа қатынасын қарастырайық:

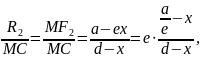
мұндағы М — эллипстің бойымен қозғалып отыратын нүкте

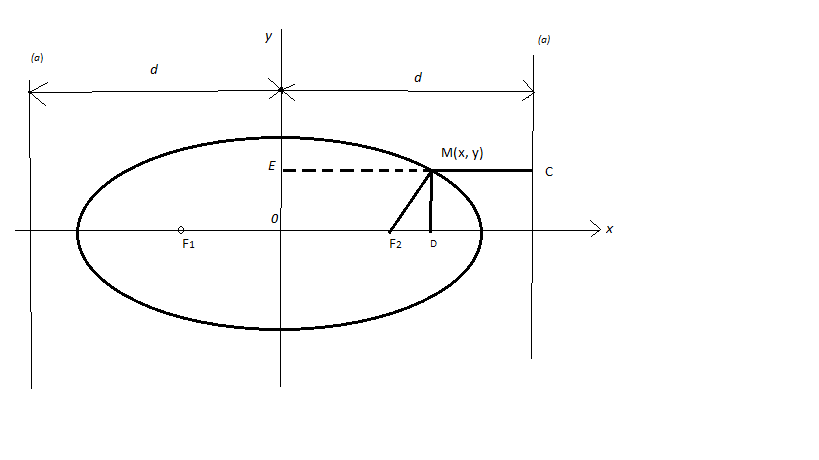
45-сызба

болғандықтан, х — айнымалы шама. Сондықтан соңғы қатынас осы х-ке тәуелді. Нүкте қозғалып, х өзгергенде бұл қатынас та өзгереді. Ендеше, бұл қатынасы х-тің функциясы.

Енді х-ке тәуелді болмайтын жағдайды қарастырайық. Бұл жоғарғы жазылған қатынастың дербес жағдайы болады. Алдыңғы айтқанымызға сәйкес ордината осіне параллель (а) түзулері де ордината осінен әр түрлі қашықтықта болады. Осы (а) түзулерінің толып жатқан әр түрлі жағдайында оның қашықтығы ордината осінен d=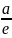 тұрақты шамасына тең болуы мүмкін, яғни жоғарғы қарастырып отырған

қатынасы эллипстің эксцентриситетіне тең.

Сонымен, ордината осіне параллель түзулердің ішіндегі бір түзудің эллипстің кіші осшен қашықтығы әрқашан да d = катынасына тең тұрақты шама болса, онда мұндай түзуді эллипстің директрисасы деп атайды. Бұл d = жағдаиында =е қатынасы х-ке тәуелді емес. Сондықтан ол эллипстің эксцентриситетіне тең. Бұл — эллипстің оң жағындағы директриса, ал оның сол жағындағы директрисаның таңбасы теріс болады, яғни d=- .

Сонымен, эллипстің әрбір нүктесінен фокусқа дейінгі қашықтықтың сол нүктеден директрисаға дейінгі қашықтыққа қатынасы әрқашан да тұрақты шама, ол эксцентриситетке тең:

=е (14 )

Директрисаның ордината осінен қашықтығының формуласы

d = ± (15)

Эллипстің эксцентриситеті е = . Осыны (15) формулаға.қойсақ:

(15´)

Эллипстің үлкен осі (2а), оның екі фокусының арасындағы қашықтықтан (2с) артық, яғни 2а>2с, а>с. Сондықтан >а. Ал директрисаның екеуі де ылғи эллипстің сыртында жатады.

9 Эллипстің түзумен қиылысуы. эллипстің теңдеуі мен у=kx+l түзуінің теңдеулері берілсін.

Эллипстің бойындағы нүктелердің ағымдық координаталары берілген түзудің теңдеуін қанағаттандырса, онда бұл екі теңдеуді біріктіріп шығарып, х арқылы өрнектейік:

Осы квадрат теңдеудегі коэффициенттерді былай белгілейік :

Cонда

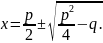
Эллипстің түзумен қиылысуы не қиылыспауы квадрат теңдеуінің дискриминантыныңи мәніне байланысты болады. Мұнда үш түрлі жағдай болуы мүмкін: 1) түзу эллипсті екі нүктеден қиып өтеді, 2) түзу эллипсті бір нүктеден жанап өтеді, 3) түзу эллипспен қиылыспайды.

Бірінші жағдайда дискриминантының нольден артық: мұнда түзу мен эллипстің қиылысатын екі нақты нүктелері бар.

Екінші жағдайда дискриминант нольге тең: , мұнда түзу эллипсті бір нүктеден жанап өтеді. Осы түзудің эллипске жанама болуы шартын табайық. Ол үшін теңдігіне p мен q-дің мәндерін қояйық.

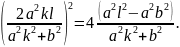
Осыдан:

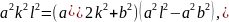
Бұл теңдік түзудің эллипске жанама болу шартын көрсетеді. Енді жанасу нүктесінің координаталарын табайық. 7-параграфта нүкте хорданы қақ бөлгенде, оның координаталары мынадай болып шыққан:

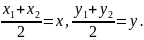
хорда жанамаға айналғанда нүктесі мен мен 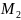нүктесінің координаталары өз ара тең болады: 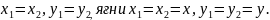Сондықтан 7-параграфтағы х теңдеулеріне (16) формуладағы 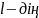мәнін қойып, жанасу нүктесінің координаталарын табайық:

Сонымен, жанасу нүктесінің координаталары мынадай болады:

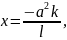
Үшініші жағдайда дискриминант нольден кем: , мұнда түзу эллипспен қиылыспайды. Ал квадрат теңдеудің түбірлері жорымал болады.

10. Эллипс пен шеңбердің параметрлік теңдеулері. Тік бұрышты координаталар системасындағы эллипстің теңдеуі берілсін:

F(x, y) (18)

Бұл теңдеудегі х пен у – белгісіз айнымалы шамалар. Осы екі айнымалы шама бір айнымалы шамаға тәуелді болсын:

Егер екі немесе онан да көп айнымалы шамалар бір айнымалы шамаға тәуелді болса, онда бұл айнымалы шамалар функция деп, ал олардың тәуелді болғані болған шамасты параметр деп аталады. (19) теңдеулердегі t-параметр, х пен y-сол параметрге тәуелді функциялар. Біз эллипстың теңдеуін жалпы түрде (18) формуламен жаздық. Енді эллипстің жабайы теңдеуін алайық :

Эллипстің бойыннан кез келген М(х, у) нүктесін алып, оны координаталардың бас нүктесімен қосып, осы М нүктесінен абсцисса осіне МD перпендикулярын түсіріп, эллипске іштей және сырттай екі шеңбер жүргізейік 46-(сызба). Бұл сызбадан: ОD=x, DM=y, DM₁=Y, M(x, y), M₁(x, Y), OE=OM₁=a, OM₂=OF=b, DM=BM₁=y.

DM₁>DM немесе У>y.

OM₁D тік бұрышты үшбұрышыннан:

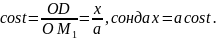
OM₂B тік бұрышты үшбұрышынан:

Сонда у= .

Сонымен, эллипстің параметрлік теңдеулері мынадай болады:

Егер а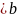 болса, онда эллипс шеңберге айналады. Шеңбердің параметрлік теңдеулері мынадай болады:

(20) теңдеудегі а мен 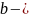эллипстің жарты осьтері, t – өзгеріліп отыратын бұрыш (46-сызба). Ал (21) теңдеудегі a-шеңбердің радиусы, t параметрі- абсцисса осі мен радиустың арасындағы бұрыш.