- •2. Практична частина:
- •Теоретична частина Статистика бюджету України
- •1.1 Роль державного бюджету України
- •1.2 Складові елементи державного бюджету України
- •1.3 Державний бюджет України
- •Кореляційне дослідження
- •2.Практична частина
- •Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4.Індекси
- •Висновки
- •Список використаної літератури:
Завдання 2
За результатами типологічного групування, що виконане в завданні 1, розрахувати:
середню кількість вантажних автомобілів для всієї сукупності і для кожної групи окремо;
моду і медіану за допомогою формул та графічно;
показники варіації кількості вантажних автомобілів: розмах варіації, середнє лінійне і квадратичне відхилення, загальну дисперсію трьома методами; коефіцієнт осциляції, квадратичний коефіцієнт варіації; групові дисперсії виробітку на 100 машинотон та середню з групових дисперсій, між групову і загальну дисперсії за цією ж ознакою та за правилом складання дисперсій перевірити рівність суми середньої з групових і між групової дисперсій загальній; коефіцієнт детермінації, емпіричне кореляційне відношення, дисперсію долі автотранспортних підприємств третьої групи.
Зробити висновки.
Таблиця 2.1
Розрахункові дані для обчислення характеристики варіації
Групи АТП за кількістю автомобілів |
Кількість авто |
Розрахункові величини
|
||||||
Середина інтервалу |
xf |
x |
|x |f |
|
х 2 |
|
||
[20-35) |
5 |
27,5 |
137,5 |
-21 |
105 |
2205 |
855,56 |
5988,92 |
[35-50) |
9 |
42,5 |
382,5 |
-6 |
54 |
324 |
1914,06 |
15312,48 |
[50-65) |
7 |
57,5 |
402,5 |
9 |
63 |
567 |
3393,06 |
10179,18 |
[65-80] |
4 |
72,5 |
290 |
24 |
96 |
2304 |
5292,56 |
37047,92 |
Всього |
25 |
- |
1212,5 |
- |
318 |
5400 |
- |
68528,5 |
Середня кількість вантажних автомобілів для всієї сукупності:
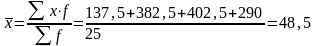 ;
де:
;
де:
х – середина інтервалу,
f – кількість АТП.
Середня кількість вантажних автомобілів для кожної групи окремо:


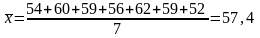

Таблиця 2.2
Дані для обчислення характеристик центру розподілу
Групи АТП за кількістю вантажівок |
Кількість АТП |
Накопичена частота |
[20-35) |
5 |
5 |
[35-50) |
9 |
14 |
[50-65) |
7 |
21 |
[65-80] |
4 |
25 |
Всього |
25 |
- |
Мода:
 де:
де:
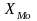 -
нижня границя модального інтервалу,
-
нижня границя модального інтервалу,
 -
розмір модального інтервалу,
-
розмір модального інтервалу,
 -
частота модального інтервалу,
-
частота модального інтервалу,
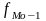 -
частота попереднього інтервалу,
-
частота попереднього інтервалу,
 -
частота інтервалу наступного за
модальним.
-
частота інтервалу наступного за
модальним.
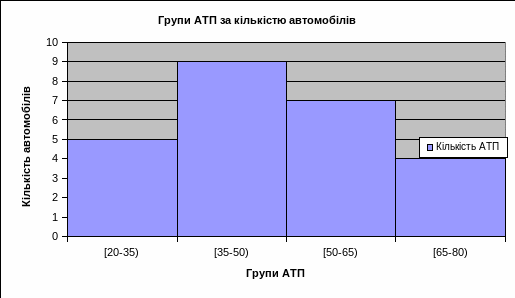
Модальний інтервал – (35-50]

Рис. 2.1 Графічне зображення моди.
Медіана:
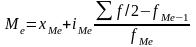 ,
де:
,
де:
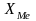 -
нижня границя медіанного інтервалу,
-
нижня границя медіанного інтервалу,
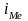 -
розмір медіанного інтервалу,
-
розмір медіанного інтервалу,
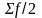 -
півсума накопичених частот,
-
півсума накопичених частот,
 -
сума накопичених частот, які передують
медіанному інтервалу,
-
сума накопичених частот, які передують
медіанному інтервалу,
 -
частота медіанного інтервалу.
-
частота медіанного інтервалу.
Медіанний інтервал: [35-50)
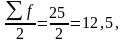 то
то

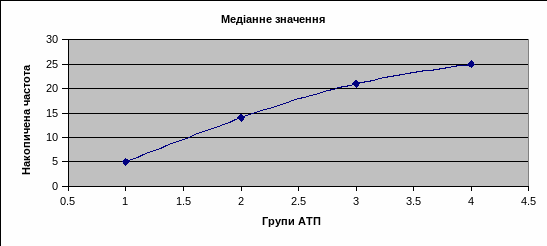
Рис. 2.2 Графічне зображення медіани
Показники варіації кількості вантажних автомобілів:
Розмах варіації


Середнє лінійне відхилення:
 ,
де:
,
де:
х – індивідуальне значення ознаки,
 -
середнє значення ознаки,
-
середнє значення ознаки,
f – частота ознаки.
Середнє квадратичне відхилення:

Визначаємо дисперсію:
А)Як квадрат квадратичного відхилення:
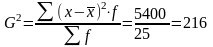
Б)Як різницю квадратів:

В)За методом моментів:
 ,
де
,
де
 і
і

За А вибираємо число, яке знаходиться посередині варіаційного ряду,
і – ширина інтервалу.
і=15; а=(42,5+57,5)/2=50

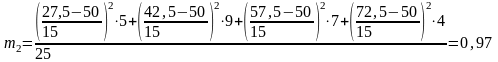
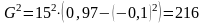
Коефіцієнт осциляції:
 де:
де:
R – розмах варіації,
– середнє значення ознаки.
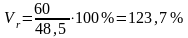
Квадратичний коефіцієнт варіації:

Оскільки
 ,
то статистична сукупність є однорідною.
,
то статистична сукупність є однорідною.
Групування АТП за виробітком на 100 машинотон:
Крок зміни (за виробітком на 100 машинотон):
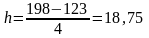
[123-141,75) = 135,123,134,138,124 (разом 5)
[141,75-160,5) =152,149,154,142,156,145, 156 (разом 7)
[160,5-179,25) = 163,175,170, 162, 167, 162, 162, 178, 164 (разом 9)
[179,25-198) = 182,198, 191, 196 (разом 4)
Таблиця 2.3
Комбінаційний розподіл АТП за кількістю автомобілів та за виробітком на сто машинотон.
АТП за кількістю автомобілів |
За виробітком на 100 машинотон, т/км |
Разом |
||||
[123-141,75) |
[141,75-160,5) |
[160,5-179,25) |
[179,25-198] |
|||
[20-35) |
3 |
- |
2 |
- |
5 |
|
[35-50) |
2 |
6 |
- |
1 |
9 |
|
[50-65) |
- |
- |
5 |
2 |
7 |
|
[65-80] |
- |
1 |
2 |
1 |
4 |
|
Разом |
5 |
7 |
9 |
4 |
25 |
|
Розрахуємо середній виробіток на 100 машинотон для всієї сукупності:
 т/км
т/км
Розрахуємо середній виробіток на 100 машинотон для кожної групи:
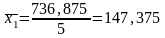
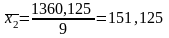

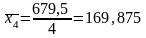
Таблиця 2.4
Розрахункові дані для обчислення групових дисперсій
Кількість вантажних автомобілів |
Виробіток на 100 машинотон |
Кількість АТП f |
Розрахункові дані |
|||||
|
|
|
|
|||||
20-35 |
123-141,75 |
3 |
132,375 |
397,125 |
-15 |
675 |
||
141,75-160,5 |
0 |
151,125 |
0 |
3,75 |
0 |
|||
160,5-179,25 |
2 |
169,875 |
339,75 |
22,5 |
1012,5 |
|||
179,25-198 |
0 |
188,625 |
0 |
41,25 |
0 |
|||
Разом |
- |
5 |
- |
736,875 |
- |
1687,5 |
||
35-50 |
123-141,75 |
2 |
132,375 |
264,75 |
-18,75 |
703,125 |
||
141,75-160,5 |
6 |
151,125 |
906,75 |
0 |
0 |
|||
160,5-179,25 |
0 |
169,875 |
0 |
18,75 |
0 |
|||
179,25-198 |
1 |
188,625 |
188,625 |
37,5 |
1406,25 |
|||
Разом |
- |
9 |
- |
1360,125 |
- |
2109,375 |
||
50-65 |
123-141,75 |
0 |
132,375 |
0 |
-42,855 |
0 |
||
141,75-160,5 |
0 |
151,125 |
0 |
-24,105 |
0 |
|||
160,5-179,25 |
5 |
169,875 |
849,375 |
-5,355 |
143,38 |
|||
179,25-198 |
2 |
188,625 |
377,25 |
13,395 |
358,85 |
|||
Разом |
- |
7 |
- |
1226,625 |
- |
502,23 |
||
65-80 |
123-141,75 |
0 |
132,375 |
0 |
-37,5 |
0 |
||
141,75-160,5 |
1 |
151,125 |
151,125 |
-18,75 |
351,56 |
|||
160,5-179,25 |
2 |
169,875 |
339,75 |
0 |
0 |
|||
179,25-198 |
1 |
188,625 |
188,625 |
18,75 |
351,56 |
|||
Разом |
- |
4 |
- |
679,5 |
- |
703,12 |
||
Всього |
|
|
|
4003,125 |
|
5002,225 |
||
Обчислимо внутрішньо групові дисперсії:
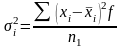 ,
де:
,
де:
 -
значення ознак окремих елементів
сукупності,
-
значення ознак окремих елементів
сукупності,
n – кількість АТП.


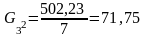
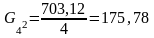
Середня з внутрішньо групових дисперсій:

Міжгрупова дисперсія:
 ,
де:
,
де:
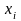 -
групові середні ,
-
групові середні ,
- загальна середня для всієї сукупності,
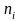 -
чисельність окремих груп.
-
чисельність окремих груп.



Перевіримо отриманий результат обчисливши загальну дисперсію, як середньозважену:

Результати майже збіглися, відхилення виникло за рахунок заокруглень.
Обчислимо коефіцієнт детермінації:
 ,
,
це означає, що 41,3% загальної дисперсії виробітку на 100 машинотон обумовлено кількістю вантажних автомобілів, а решта зумовлено іншим фактором.
Емпіричне кореляційне відношення:
 ,
,
тобто залежність між середнім виробітком на 100 машинотон і кількістю вантажних автомобілів становить 64%.
Розрахуємо дисперсію частин АТП третьої групи.
Частка підприємств третьої групи складає:

Тоді дисперсія:

Висновок:
Згідно обрахунків досліджувана статистична сукупність є однорідною.
Середня кількість вантажних автомобілів для всієї сукупності становить 48,5. Мода встановилась на рівні 50; а медіана 44. Обчислення були достатньо точними, про що свідчить невелика розбіжність між значеннями величин обрахованих різними способами. Залежність між середнім виробітком на 100 машинотон і кількістю вантажних автомобілів становить 64%.

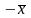
 ƒ
ƒ ƒ
ƒ