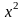- •2. Практична частина:
- •Теоретична частина Статистика бюджету України
- •1.1 Роль державного бюджету України
- •1.2 Складові елементи державного бюджету України
- •1.3 Державний бюджет України
- •Кореляційне дослідження
- •2.Практична частина
- •Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4.Індекси
- •Висновки
- •Список використаної літератури:
Кореляційне дослідження
Дослідимо залежність індексу продукції промисловості від доходів населення.
Для визначення залежності між даними показниками скористаємось формулою:
Ŷх = a0 + a1x,
Де Ŷх – вирівняне значення індексу продукції промисловості.
х – величина доходу населення.
а0, а1 – шукані параметри.
Таблиця 1.
Розрахункова таблиця для обчислення показників кореляції
Роки
|
Доходи Населення млрд. грн. (х) |
Індекс продукції промисловостї % (у)
|
Розрахункові дані |
|||
ху |
|
|
Ух |
|||
2008 |
845,6 |
94,8 |
80162,88 |
715039,36 |
8987,04 |
94,79 |
2009 |
894,3 |
78,1 |
69844,83 |
799772,49 |
6099,61 |
95,39 |
2010 |
1101,2 |
111,2 |
122453,44 |
1212641,44 |
12365,44 |
97,95 |
2011 |
1266,8 |
107,6 |
136307,68 |
1904782,24 |
11577,76 |
100,01 |
2012 |
1407,2 |
98,2 |
138187,04 |
1980211,84 |
9643,24 |
101,75 |
Разом |
5515,1 |
489,9 |
546955,87 |
6612447,37 |
48673,09 |
489,9 |
Середні |
1103,02 |
97,98 |
109391,174 |
1322489,474 |
9734,618 |
97,98 |
Параметри рівняння зв’язку визначимо способом найменших квадратів з складеної системи рівнянь з двома невідомими:
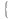
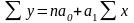





Розв’язавши дану систему рівнянь, отримуємо такі параметри:

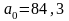
Параметри а0 та а1 можна розрахувати за формулами:
 ;
;
 .
.
Тоді лінійне рівняння зв’язку між середньомісячним доходом населення за видавничою діяльністю буде мати наступний вигляд:

Отже, зі зростанням діяльності середньомісячна заробітна плата найманих працівників за видавничою діяльністю зросте на 0,0124 грн.
Послідовно підставивши в дане рівняння значення факторної ознаки х, отримаємо теоретичні значення результативної ознаки Yх:
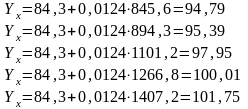
Тепер зобразимо залежність наочно, скориставшись графіком:
Графік залежності індексу продукції промисловості від доходів населення

Обчислення лінійного коефіцієнта кореляції.
Обчислимо:



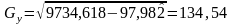
Лінійний коефіцієнт кореляції:


Зв’язок
прямий r>0 і тісний |r|
R=r^2=0,03^2=0,0009
Висновок: Отже, зміни доходів населення населення на 0,09% впливає на індекс продукції промисловості.
2.Практична частина
Варіант 1 [1-25]
Завдання 1
На основі даних по 25 автотранспортним підприємствам (АТП) необхідно виконати:
Групування АТП за кількістю вантажних автомобілів, виділивши чотири групи з рівними інтервалами. Для кожної групи підрахувати число АТП, питому вагу групи в загальній чисельності АТП, кількість вантажних автомобілів в середньому на одне АТП, середню продуктивність та середній процент використання вантажних автомобілів. Результати групування представити у вигляді таблиці (оформленої з урахуванням всіх правил оформлення статистичних таблиць) і проаналізувати.
Здійснити комбінаційний розподіл АТП за кількістю вантажних автомобілів і коефіцієнтом використання вантажних автомобілів, використовуючи результати першого групування та утворюючи чотири групи за другою ознакою. Охарактеризувати одержані групи і підгрупи рядом показників, необхідних для аналізу. Зробити висновки.
Вихідні дані:
Таблиця 1.1.
Дані про автотранспортні підприємства
№ автопідприємства |
Кількість вантажних автомобілів |
Коефіцієнт використання вантажівок |
Виробіток на 100 машинотонн, т/км |
1 |
33 |
67 |
135 |
2 |
46 |
60 |
123 |
3 |
32 |
66 |
134 |
4 |
54 |
69 |
163 |
5 |
39 |
67 |
152 |
6 |
41 |
68 |
149 |
7 |
35 |
67 |
154 |
8 |
60 |
73 |
175 |
9 |
41 |
72 |
182 |
10 |
80 |
61 |
142 |
11 |
34 |
66 |
170 |
12 |
67 |
77 |
198 |
13 |
46 |
69 |
156 |
14 |
20 |
64 |
138 |
15 |
70 |
68 |
162 |
16 |
23 |
72 |
167 |
17 |
48 |
65 |
124 |
18 |
36 |
67 |
145 |
19 |
59 |
78 |
162 |
20 |
46 |
63 |
156 |
21 |
56 |
66 |
162 |
22 |
62 |
80 |
191 |
23 |
59 |
63 |
196 |
24 |
68 |
72 |
178 |
25 |
52 |
68 |
164 |
Крок зміни (за кількістю вантажних автомобілів):
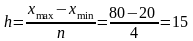
де: хmax , xmin – максимальне і мінімальне значення ознаки;
n – кількість груп.
I група - [20-35) = 33, 32, 34, 20, 23.
II група - [35-50) = 46, 39, 41, 35, 41, 46, 48, 36, 46.
III група - [50-65) = 54, 60, 59, 56, 62, 59, 52.
IV група - [65-80] = 80, 67, 70, 68.
Число АТП для кожної групи:
I – 5
II – 9
III – 7
IV – 4
Питома вага групи в загальній чисельності АТП:
100% – 25
 %
– 5
%
– 5
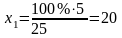 %
%
100% – 25
 %
– 9
%
– 9
 %
%
100% – 25
 %
– 7
%
– 7
 %
%
100% – 25
 %
– 4
%
– 4
 %
%
Кількість вантажних автомобілів в середньому на одне АТП для кожної групи:
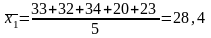 ;
;
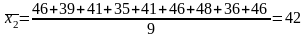 ;
;
 ;
;
 .
.
Середня продуктивність використання ватажних автомобілів для кожної групи:
 ;
;
 ;
;
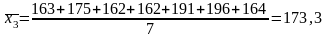 ;
;
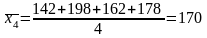 .
.
Середній процент використання вантажних автомобілів для кожної групи:
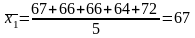 ;
;
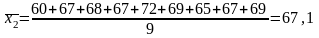 ;
;
 ;
;
 .
.
Групування АТП за кількістю вантажних автомобілів наведений у таблиці 1.2
Таблиця 1.2
Групування АТП за кількістю вантажних автомобілів
№ Групи |
Розподіл АТП за кількістю вантажних автомобілів |
Кількісь АТП
|
Питома вага , % |
Середня кількість вантажних автомобілів на одне АТП |
Середня продукти-вність |
Середній процент використання автомобілів |
1 |
[20-35] |
5 |
20 |
28,4 |
148,8 |
67 |
2 |
[35-50] |
9 |
36 |
42 |
149 |
67,1 |
3 |
[50-65) |
7 |
28 |
57,4 |
173,3 |
71 |
4 |
[65-80] |
4 |
16 |
71,3 |
170 |
69,5 |
За даними таблиці найбільшу кількість АТП має друга група – 9. Найбільша питома вага у другої групи – 36%. Найбільша кількість вантажних автомобілів в середньому на одне АТП у четвертої групи – 71,3, а найменше у першої – 28,4. Найбільша середня продуктивність у третьої групи – 173,3, а найменша у першої – 148,8. Найбільший середній процент використання автомобілів у третьої групи – 71, а найменший у першої – 67.
Крок зміни (за коефіцієнтом використання вантажних автомобілів):
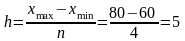
[60-65) = 60, 61, 64, 63, 63.
[65-70) = 67, 66, 69, 67, 68, 67, 66, 69, 68, 65, 67, 66, 68.
[70-75) = 73, 72, 72, 72.
[75-80] =77, 78, 80.
Комбінаційний розподіл АТП за кількістю вантажних автомобілів і коефіцієнтом використання вантажних автомобілів наведений у таблиці1.3.
Таблиця 1.3
Комбінаційний розподіл АТП
Кількість вантажних автомобілів |
Коефіцієнт використання автомобілів |
Разом |
|||
[60-65)
|
[65-70)
|
[70-75) |
[75-80]
|
||
[20-35) |
1 |
3 |
1 |
- |
5 |
[35-50) |
2 |
6 |
1 |
- |
9 |
[50-65) |
1 |
3 |
1 |
2 |
7 |
[65-80] |
1 |
1 |
1 |
1 |
4 |
Разом |
5 |
13 |
4 |
3 |
25 |
Висновок:
Згідно комбінаційного розподілу ми можемо зробити висновок, що більшим попитом користуються АТП з кількістю 35-50 машин, а найбільш розповсюджений коефіцієнт використання 65-70.