Задача 2

Для десяти цехів машинобудівного підприємства наведено такі дані (табл. 2). Побудувати багатофакторну лінійну регресію, яка описуватиме зв’язок продуктивності праці з наведеними чинниками.

Таблиця 2. Вихідні дані задачі

Номер цеху	Продуктивність праці, тис. грн.	Середньомісячна зарплата, грн.	Фондомісткість продукції, тис. грн.	Виконання норми виробітку , %
1	45	2120	0,20	130
2	42	1888	0,04	127
3	50	2056	0,30	151
4	55	2232	0,20	149
5	40	1808	0,10	140
6	70	2800	0,10	141
7	56	2224	0,25	152
8	57	2096	0,03	188
9	55	2152	0,15	120
10	53	2000	0,32	126

Розв’язання

Продуктивність праці залежить від трьох чинників – середньомісячної зарплати, фондомісткості продукції та відсотку виконання норми виробітку. Загальний вигляд трифакторної регресійної лінійної моделі буде такий:

,

де – продуктивність праці, тис. грн.; – середньомісячної зарплата, грн., – фондомісткість продукції, тис. грн., – відсоток виконання норми виробітку; – стохастична складова, – параметри моделі, а вибіркової регресійної моделі:

,

де – оцінки параметрів моделі.

Щоб мати явний вигляд залежності, необхі­дно знайти (оцінити) невідомі параметри за МНК.

Введемо допоміжну змінну , яка відповідатиме параметру і запишемо модель в матричному вигляді: . Тоді оцінки параметрів можна знайти за формулою:

;

;

Виконавши необхідні розрахунки, отримуємо:

В результаті модель має вигляд:

Виконаємо перевірку статистичної значимості оцінок параметрів моделі за допомогою t-критерію Стьюдента. Для цього виконаємо необхідні розрахунки:

; ; ;

; ; ;

Коли стандартні помилки параметрів більші за абсолютні значення оцінок цих параметрів, то це може означати, що оцінка параметра є зміщеною. Якщо, наприклад, стандартна помилка на 10 % перевищує абсолютне значення оцінки параметра, то можна говорити про те, що цей параметр має зміщення щодо його істинного значення. Така ситуація спостерігається стосовно оцінки і її стандартної помилки : або .

Критичне значення критерію Ст’юдента для рівня значимості та ступенів вільності ( – кількість параметрів ) знаходимо за допомогою таблиць –розподілу Ст’юдента: .

Оскільки, < , то оцінка вважається статистично значимою, тобто, зі ймовірністю 95% вплив рівня середньомісячної зарплати на продуктивність праці визнається істотним. > , > , > , тому оцінки зі ймовірністю 95% не є статистично значимими, що підтверджує нульову гіпотезу про неістот­ність впливу змінних та на результативну ознаку .

Довірчі межі коефіцієнтів регресії зі ймовірністю 0,95:

або

або

або

або

Коефіцієнт детермінації використовується як критерій щільності зв’язку між залежною та незалежними змінними:

З цього випливає, що варіація залежної змінної на 86% визначається варіацією незалежних змінних.

З урахуванням кількості чинників та кількості спостережень обчислимо скоригований коефіцієнт детермінації:

Виконаємо перевірку моделі на адекватність за –критерієм Фішера.

Задаємо рівень значимості: .

За статистичними таблицями –розподілу Фішера з ступенями вільності та заданим рівнем значимості знаходимо критичне значення критерію: . , то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною.

Оскільки побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Припустимо, нам відомі значення чинників в період – , тоді ми можемо отримати прогнозне значення :

Інтервальні прогнози результативної змінної з рівнем довіри для побудованої моделі:

для індивідуального значення:

;

для математичного сподівання:

	A	D	C	D	E	F	G	h	J	I	K
1	Обласні філіїї банку	Кредитовий оборот, млн. грн.у	Чисельність клієнтів банку, тис. осіб, х
2	1,0	7,4	6,0	7,9	0,2	1,8	6,0	9,7	0,6	7,3	8,4
3	2,0	7,2	5,0	6,9	0,4	1,8	5,1	8,7	0,6	6,3	7,5
4	3,0	8,6	7,0	8,8	2,0	1,9	7,0	10,7	0,7	8,1	9,6
5	4,0	9,5	8,0	9,8	5,8	2,0	7,8	11,8	1,0	8,8	10,8
6	5,0	4,6	4,0	5,9	2,6	1,9	4,0	7,8	0,8	5,1	6,7
7	6,0	7,3	5,0	6,9	0,4	1,8	5,1	8,7	0,6	6,3	7,5
8	7,0	8,6	7,0	8,8	2,0	1,9	7,0	10,7	0,7	8,1	9,6
9	8,0	9,8	7,0	8,8	2,0	1,9	7,0	10,7	0,7	8,1	9,6
10	9,0	7,0	4,0	5,9	2,6	1,9	4,0	7,8	0,8	5,1	6,7
11	10,0	4,8	3,0	4,9	6,8	2,0	2,9	7,0	1,1	3,9	6,0
12	Сума	74,8	56		24,4
13	Середнє значення	7,5	5,6
14	Σ ху=	442,70		b1=	0,98	b1=	0,98
15	Σ х2=	338,00		b0=	2,01	b0=	2,01
16	Е =	0,73
17
18		4,54			0,57		6,40
19		24,40			0,02		2,27
20					0,79	tкр.=	2,31
21	r =	0,91
22	R2 =	0,84
23	F =	85,73
24	Fкр. =	5,32

Умова задачі 2:

Визначити параметри лінійної моделі залежності витрат на споживання ( С ) від рівня доходів ( D ), збережень ( S ) та заробітної плати ( L ).

а) виконати перевірку статистичної значимості оцінок параметрів, знайдених за методом найменших квадратів, та знайти інтервали довіри для параметрів ₀,₁, ₂,β₃;

б) знайти коефіцієнти еластичності та стандартизовані коефіцієнти, пояснити їх зміст;

в) знайти множинні коефіцієнти кореляції та детермінації. За допомогою знайдених коефіцієнтів описати вплив розглядуваних факторів на результат;

г) перевірити модель на адекватність;

д) знайти інтервальні прогнози індивідуального значення та математичного сподівання для деякої трійки значень змінних D, S, L.

Обчислення виконати на базі n статистичних даних для певного регіону.

i	C, млн. грн.	D, млн. грн.	S, млн. грн.	L, млн. грн.
1	22,0	65,0	36,2	12,5
2	23,1	66,5	24,9	10,6
3	25,0	66,0	35,2	13,4
4	24,3	64,9	36,7	15,5
5	23,5	68,1	38,0	14,5
6	25,5	67,2	35,9	16,5
7	26,3	69,0	38,5	16,8
8	20,0	74,2	39,0	17,0
9	27,0	75,5	39,5	18,5
10	29,0	80,5	38,2	20,0

Розв'язання.

Лінійна модель залежності витрат на споживання ( С ) від рівня доходів ( D ), збережень ( S ) та заробітної плати ( L ) матиме виглляд:

C = ₀ + ₁D +₂S +β₃L + u, де С – результативна змінна, D, S, L – незалежні змінні, ₀,₁, ₂,β₃ - параметри моделі, u – стохастична складова моделі.

Оцінки параметрів моделі знаходимо за допомогою МНК.

Для цього перейдемо до позначень:

C = y, D = x₁, S = x₂, L = x₃ і запишемо модель в матричній формі:

Y = X*В + U, де Y – вектор значень залежної змінної, В – вектор параметрів моделі, Х – матриця значень незалежної змінної, U – вектор залишків.

Оцінку вектора параметрів моделі знайдемо за формулою:

Необхідні розрахунки подані нижче.

Транспонована матриця факторів:

	1	1	1	1	1	1	1	1	1	1
Х/ =	65	66,5	66	64,9	68,1	67,2	69	74,2	75,5	80,5
	36,2	24,9	35,2	36,7	38	35,9	38,5	39	39,5	38,2
	12,5	10,6	13,4	15,5	14,5	16,5	16,8	17	18,5	20

10,00	696,90	362,10	155,30
696,90	48815,85	25321,81	10931,35
362,10	25321,81	13271,93	5704,87
155,30	10931,35	5704,87	2484,41

53,68	-0,81	-0,68	1,75
-0,81	0,01	0,01	-0,03
-0,68	0,01	0,02	-0,03
1,75	-0,03	-0,03	0,09

245,70

17178,87

8918,70

3854,35

32,22

-0,18

-0,40

1,25

В =

В результаті модель має вигляд: Ĉ(і)=32,22-0,18 D(i) – 0,40S(i) + 1,25L (i).

Перевіримо значущість оцінок параметрів b₀,b₁, b₂, b₃. Як і у випадку простої лінійної регресії, виконаємо перевірку їх істотності за допомогою t-критерію Стьюдента:

де с_ii – діагональний елемент матриці ^-1. Знаменник відношення називається стандартною помилкою оцінки параметра моделі.

Незміщена оцінка дисперсії залишків:

=5,16.

Для b₁:

Обчислене значення критерію порівнюється з табличним при вибраному рівні значущості і n-k ступенях свободи. Якщо t_факт. < t_крит. , то відповідна оцінка параметра економетричної моделі є достовірною тобто, оцінки параметрів характеризують істотній зв’язок відповідних незалежних змінних із залежною.

t_крит. =2,447. Очевидно, що критичне значення критерію більше за фактичне значення, розраховане для параметра b₁, тому дана оцінка характеризує не істотний зв’язок між змінною х₁ та результатом. Перевірка статистичної значимості інших оцінок параметрів здійснюється аналогічно.

На основі t-критерію і стандартної помилки побудуємо довірчі інтервали для парамеирів β_i:

Параметр β₁ зі ймовірністю 0,95 знаходиться в інтервалі: β₁= -0, 18 ± 0,67.

Аналогічно виконуємо перевірку статистичної значимості оцінок інших оцінок параметрів та знаходимо їх довірчі межі .

Характеристиками відносної зміни результату за рахунок факторів є коефіцієнти еластичності:

які показують, на скільки процентів у середньому змінюється результативна ознака зі зміною факторної на 1%.

Коефіцієнт еластичності, який характеризує вплив фактора х₁ на результативну змінну: тобто, при збільшенні рівня доходів на 1% споживання гранично зменшиться на 0,51%.

Коефіцієнти еластичності за іншими факторами знаходимо аналогічно.

Числове значення коефіцієнта детермінації характеризує якою мірою варіація залежної змінної (С) визначається варіацією незалежних змінних. Чим ближчий він до 1, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Розраховують коефіцієнт детермінації без урахування числа ступенів свободи за формулою:

або як і у випадку лінійної парної регресії

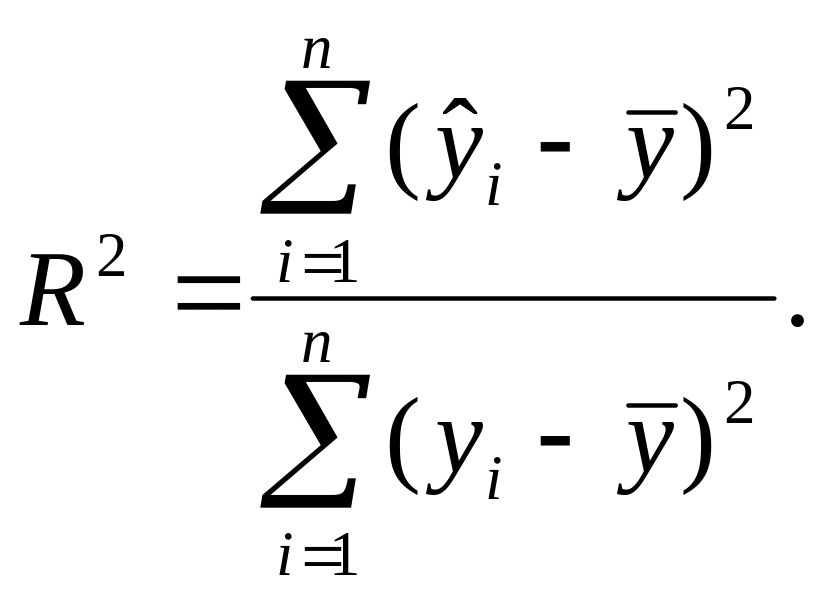
є ( 0 ; 1 ). Коли виникає питання порівняння значень коефіцієнтів детермінації в різних моделях, то слід враховувати кількість змінних, які пояснюють результат. В цьому випадку коефіцієнт детермінації коригують з урахуванням факторів, які входять до моделей.

Скоригований коефіцієнт детермінації розраховують за формулою:

В нашому випадку: 0,49, 0,23.

Отже, вибранні пояснювальні змінні не найкращим чином пояснюють варіацію результативної змінної, тобто зв’язок між незалежними змінними і залежною помірний.

Для перевірки адекватності багатофакторної моделі, як і у випадку простої лінійної моделі, використовується F - критерій Фішера. Розраховується F - статистика Фішера з n-k та k-1 ступенями вільності:

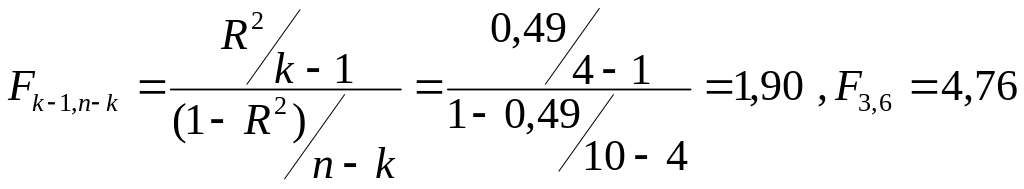для рівня значимості α=0,99. Оскільки фактичне значення критерію Фішера, розраховане для побудованої моделі менше критичного значення для рівня значимості α=0,99, то зі ймовірністю 0,99 побудовану модель вважатимемо не адекватною, тобто такою, що не відповідає дійсності.

Побудована модель виявилася не адекватною, тому використовувати її в прогнозуванні не рекомендується. Але для прикладу знайдемо прогнозні значення результативної змінної для побудованої моделі за формулами:

для індивідуального значення залежної змінної інтервальний прогноз:

для математичного сподівання:

Для D = 80, S = 38, L = 20 зі ймовірністю 0,95 маємо:

для індивідуального значення залежної змінної інтервальний прогноз:

для математичного сподівання:

	B	C	D	E	F	G	H	I
31	х=	1,00	80,50	38,20	20,00
32		1
33	х/=	80,5			-2,135732506	0,037623	-0,02498	0,033373023
34		38,2			0,606175573
35		20
36	20,37447	≤ у10 ≤	34,466195;	23,09184	≤ у10 ≤	31,74883
37