Трохи теорії

На практиці економічні процеси змінюються під впливом багатьох різноманітних факторів. Багатофакторний регресіцний аналіз допомагає знайти явний вигляд таких залежностей та кількісно оцінити вплив різних факторів на досліджуваний процес.

Узагальнена багатофакторна регресійна лінійна модель має вигляд: y = β₀ + β₁x₁ +...+β_рх_р+ u, де y- результативна змінна; х₁, х₂, ..., х_р - факторні змінні; u – стохастична складова, яка вводиться до моделі з метою урахувати наявність впливу факторів, які не входять до моделі, β₀ , β₁ ,..., β_р –параметри моделі, а вибіркова регресійна модель - = b₀ + b₁x₁+...+b_рх_р, де b₀, b₁,..., b_р – оцінки параметрів моделі.

Щоб мати явний вигляд залежності, необхі­дно знайти (оцінити) невідомі параметри b₀, b₁,..., b_р цієї моделі.

Як і у випадку простої лінійної регресії, невідомі оцінки параметрів знаходять за методом найменших квадратів.

Введемо допоміжну змінну х₀, яка відповідатиме параметру β₀ і запишемо модель багатофакторної лінійної регресії для кожного спостереження:

Розглянемо позначення:

матрицю результатів – вектор-стовпчик розмірності спостережень за незалежною змінною матрицю факторів (враховуючи допоміжну змінну, значення якої для кожного спостереження дорівнює одиниці, ) – матрицю розмірності n спостережень за незалежними змінними матриця параметрів – вектор розміру матриця випадкових величин – вектор розмірності

Виходячи з наведених позначень

Цей вираз зручно записати у матричному вигляді Y = X^.В + U.

Оцінку вектора параметрів моделі можна знайти за формулою:

Перевірка значимості оцінок параметрів b₀,b₁, b₂, b₃. аналогічна як і у випадку простої лінійної регресії. Виконують її для кожного параметра окремо. Використовується t-критерій Стьюдента:

де с_ii – діагональний елемент матриці ^-1, . Знаменник відношення називається стандартною помилкою оцінки параметра моделі.

Незміщена оцінка дисперсії залишків:

Обчислене значення критерію порівнюється з табличним при вибраному рівні значущості і n-k ступенях свободи. Якщо t_факт. < t_крит. , то відповідна оцінка параметра економетричної моделі є достовірною тобто, оцінки параметрів характеризують істотній зв’язок відповідних незалежних змінних із залежною.

На основі t-критерію і стандартної помилки можна знайти довірчі інтервали для параметрів β_i:

Характеристиками відносної зміни результату за рахунок факторів є коефіцієнти еластичності:

які показують, на скільки процентів у середньому змінюється результативна ознака зі зміною факторної на 1%.

Числове значення коефіцієнта детермінації характеризує якою мірою варіація залежної змінної визначається варіацією незалежних змінних. Чим ближчий він до 1, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Розраховують коефіцієнт детермінації без урахування числа ступенів свободи за формулою:

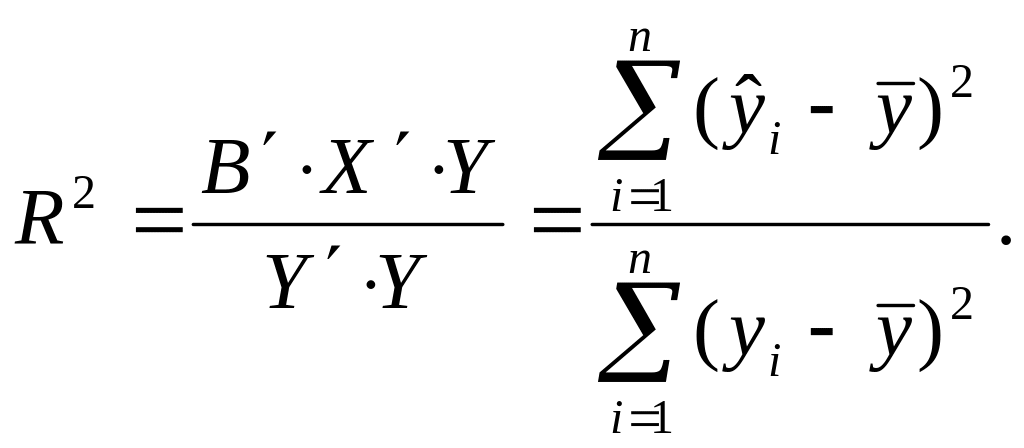
є ( 0 ; 1 ). Коли виникає питання порівняння значень коефіцієнтів детермінації в різних моделях, то слід враховувати кількість змінних, які пояснюють результат. В цьому випадку коефіцієнт детермінації коригують з урахуванням факторів, які входять до моделей. Скоригований коефіцієнт детермінації розраховують за формулою:

Для перевірки адекватності багатофакторної моделі, як і у випадку простої лінійної моделі, використовується F - критерій Фішера. Розраховується F - статистика Фішера з n-k та k-1 ступенями вільності:

В цій формулі n, k – кількість спостережень та кількість параметрів відповідно.

Фактичне значення даного критерію порівнюється з критичним для заданого рівня значимості α. Якщо F_кр< F_факт, то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною. Або навпаки, якщо F_кр> F_факт.

Якщо побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Інтервальні прогнози результативної змінної для побудованої моделлі обчислюються за формулами:

для індивідуального значення залежної змінної:

для математичного сподівання: