3.3. Расчет плотности тока без учета поверхностного эффекта
Для случаев
(соответственно
частота f1=1
кГц) и
(соответственно частота f2=5
кГц) поверхностный эффект практически
отсутствует. Считаем, что величина
амплитуды плотности тока
постоянна в любой точке поперечного
сечения проводника и равна величине
на поверхности шины.
В итоге, распределение нормированной
амплитуды плотности тока по сечению
шины без учета поверхностного эффекта
.
Расчетные точки этой прямой
(рис. 6. 7.) представлены в табл. 3, 4 (столбец 2, 3) при глубине проникновения волны (м) и соответствующей частоте f1 = 1 кГц, а также при глубине проникновения волны (м) и соответствующей частоте f2 = 5 кГц.
Расчет плотности тока с учетом поверхностного эффекта
Найдем комплексную амплитуду плотности
тока с помощью уравнения Максвелла
.
Но
,
поэтому
.
Решением первого уравнения Максвелла,
являющего линейным дифференциальным
уравнением второго порядка, будет
.
В декартовой системе координат
записывают в виде следующего определителя:
.
Учитывая, что
,
имеем
.
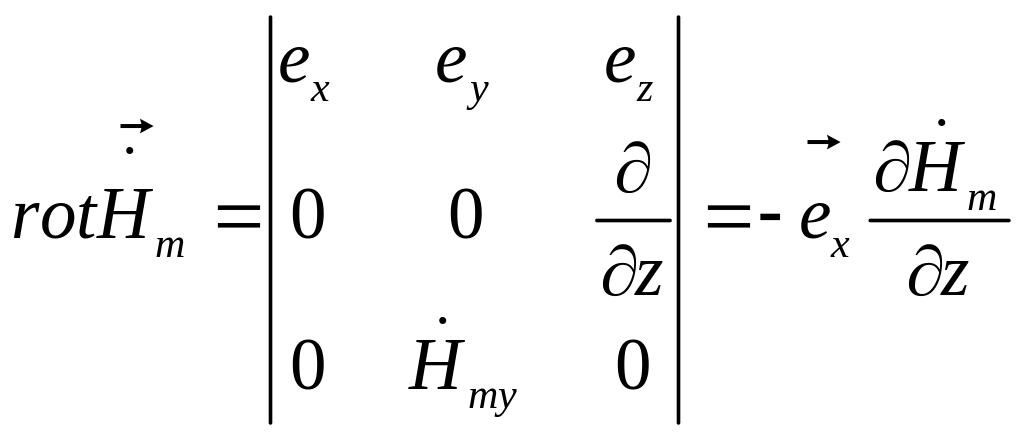
Выделим действительную и мнимую части полученного выражения. Для этого перепишем его в виде:
.
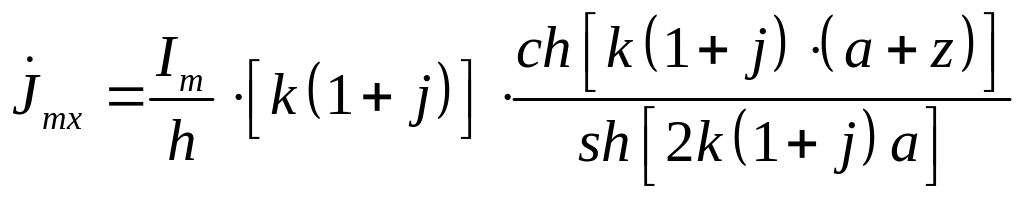Вычислим модуль
.
Переходим к переменной
:
;
.
Возвращаемся к старой переменной:
На поверхности проводника
.
Вычислим модуль
:
;
.
В итоге, распределение нормированной амплитуды плотности тока по сечению левой шины с учетом поверхностного эффекта
.
По расчетным точкам этой кривой, представленным в табл. 3 (столбцы 4 – 7) строим кривые (рис. 6) при соответствующих частотах.
Табл. 3. Расчетные значения распределения нормированной амплитуды
в левой шине для заданных частот.
f, кГц
z, ×10-3 м. |
1 |
5 |
18 |
40 |
70 |
100 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
-0,50 |
1,000 |
0,275 |
0,102 |
0,039 |
0,018 |
|
-0,40 |
0,276 |
0,102 |
0,039 |
0,018 |
||
-0,30 |
0,278 |
0,106 |
0,044 |
0,022 |
||
-0,20 |
0,287 |
0,122 |
0,060 |
0,035 |
||
-0,10 |
0,311 |
0,157 |
0,090 |
0,058 |
||
0 |
0,355 |
0,214 |
0,138 |
0,098 |
||
0,10 |
0,426 |
0,296 |
0,207 |
0,153 |
||
0,20 |
0,525 |
0,405 |
0,308 |
0,244 |
||
0,30 |
0,651 |
0,551 |
0,456 |
0,391 |
||
0,40 |
0,809 |
0,743 |
0,675 |
0,625 |
||
0,50 |
1,000 |
1,000 |
1,000 |
1,000 |
||
рис. 6. Графики зависимости нормированной амплитуды
в левой шине для заданных частот
Аналогично, распределения нормированной амплитуды плотности тока по сечению правой шины с учетом поверхностного эффекта
.
Табл. 4. Расчетные значения распределения нормированной амплитуды
в правой шине для заданных частот
f, кГц
z, ×10-3 м. |
1 |
5 |
18 |
40 |
70 |
100 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
-0,50 |
1,000 |
1,000 |
1,000 |
1,000 |
1,000 |
|
-0,40 |
0,809 |
0,743 |
0,675 |
0,625 |
||
-0,30 |
0,651 |
0,551 |
0,456 |
0,391 |
||
-0,20 |
0,525 |
0,405 |
0,308 |
0,244 |
||
-0,10 |
0,426 |
0,296 |
0,207 |
0,153 |
||
0 |
0,355 |
0,214 |
0,138 |
0,095 |
||
0,10 |
0,311 |
0,157 |
0,090 |
0,058 |
||
0,20 |
0,287 |
0,122 |
0,060 |
0,035 |
||
0,30 |
0,278 |
0,106 |
0,044 |
0,022 |
||
0,40 |
0,276 |
0,102 |
0,039 |
0,018 |
||
0,50 |
0,275 |
0,102 |
0,039 |
0,018 |
||
рис. 7. Графики зависимости нормированной амплитуды
в правой шине для заданных частот