Министерство Культуры Российской Федерации

Государственное Образовательное Учреждение

«Санкт-Петербургский Государственный Университет

Кино и Телевидения»

Кафедра акустики

Электродинамика и распространение радиоволн

Выполнил:

студент III-го курса ФАВТ,

заочное отделение,

шифр:

С-Петербург

2008

ОГЛАВЛЕНИЕ

1. Задание……………………………………………………………………………........ 3

2. Введение……………………………………………………………………………….. 4

3. Основная часть………………………………………………………………………… 7

3.1 Расчёт напряженности магнитного поля…………………………………………….. 7

3.2 Расчёт плотности тока без учёта поверхностного эффекта………………………… 9

3.3 Расчёт плотности тока с учётом поверхностного эффекта…………………………. 9

3.4 Расчёт активного и реактивного сопротивлений шины…………………………….. 13

4. Заключение……………………………………………………………………………... 15

5. Литература……………………………………………………………………………… 16

1. Задание

Вариант №21

Переменный ток протекает вдоль длинной плоской металлической шины (рис. 1).

1). Высота шины – мм , толщина – мм, причём 2а <<h. Удельная проводимость и магнитная проницаемость материала шины соответственно равны и . На расстоянии b расположена, точна такая же шина с обратным током, причём b << h. Считая, что на расстоянии 2а от поверхности шины магнитное поле однородно и равно магнитному полю на поверхности, определить наиболее рациональным способом:

- распределение нормированной амплитуды напряжённости магнитного поля по сечению шины ( , где - значение амплитуды напряжённости магнитного поля на поверхности шины). Построить графики для заданных частот , , , , , кГц;

- распределение нормированной амплитуды плотности тока по сечению шины ( , где - амплитуда плотности тока на поверхности шины). Построить графики для заданных частот;

-активное и реактивное сопротивления шины на единицу её длины для заданных частот

Построить графики зависимости активного и реактивного сопротивлений шины от частоты.

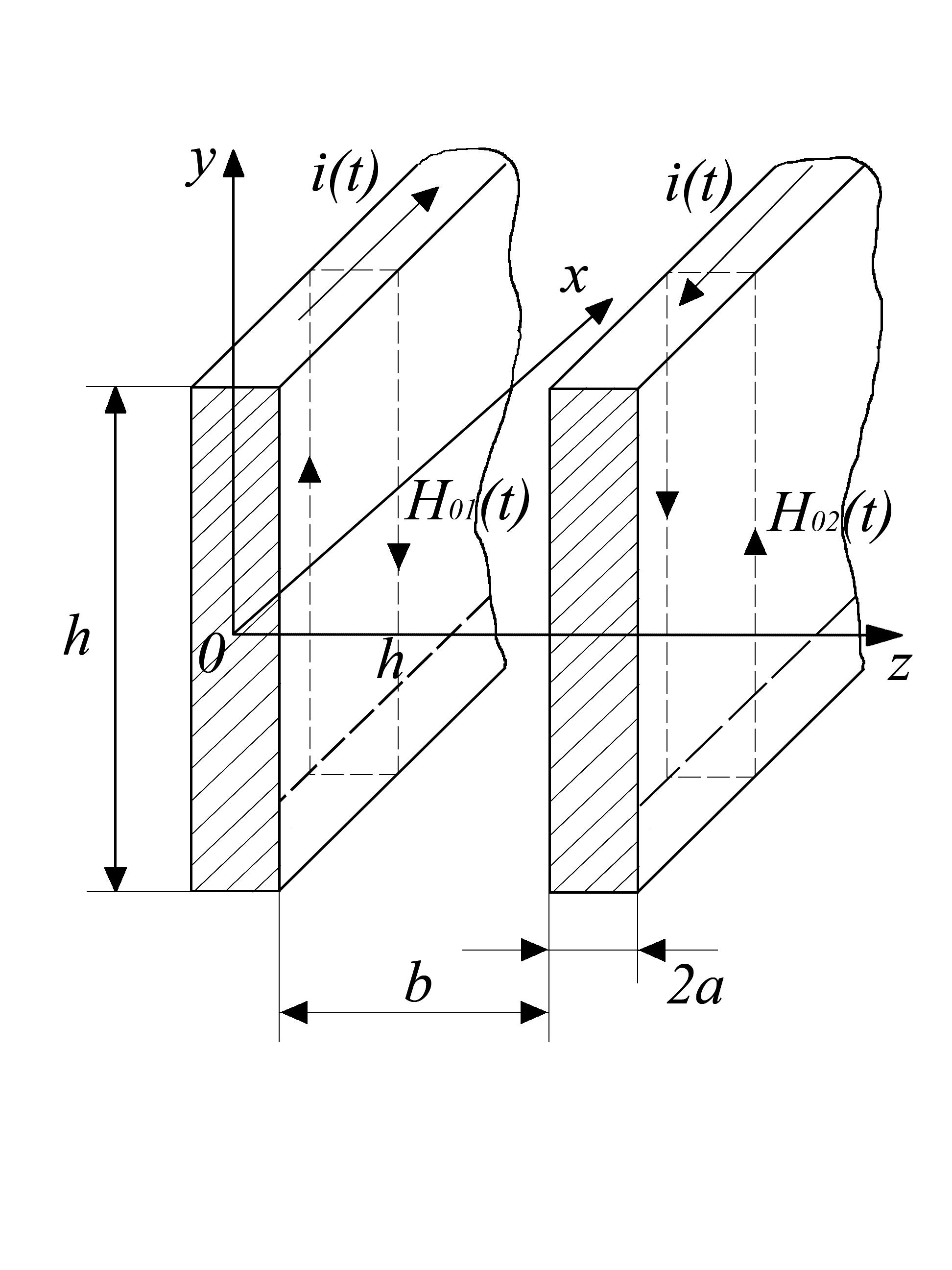
Рис. 1. Две длинные плоские металлические шины

2.Введение

Основная цель работы - получение необходимых навыков исследования и практического расчёта электромагнитного поля в одномерных задачах, когда и зависят только от одной пространственной координаты, обобществление полученных теоретических навыков и формализация методов расчёта отдельных характеристик электромагнитного поля.

Основными уравнениями электродинамики являются уравнения Максвелла, устанавливающие связь между основными характеристиками электромагнитного поля , , , , и электрическим зарядом в рассматриваемой точке , которые можно представить в дифференциальной форме:

, , , ,

где и - вектора напряжённости электрического и магнитного полей; и -вектора электрической и магнитной индукции; - вектор плотности тока проводимости;

- объёмная плотность заряда.

Между основными характеристиками электромагнитного поля существуют связи, учитывающие электромагнитные параметры вещества, в котором исследуется поле:

, , ,

где ε, µ – абсолютные диэлектрическая и магнитная проницаемости вещества;

γ- удельная проводимость.

Так как в данной курсовой работе вектора электромагнитного поля изменяются во времени по гармоническому закону, то применяются уравнения Максвелла в комплексной форме:

, , , .

В проводящих средах даже при весьма высоких частотах плотность тока смещения пренебрежимо мала по сравнению с плотностью тока проводимости . В среде с удельной проводимостью и магнитной проницаемостью для монохроматических полей первое второе уравнения Максвелла для комплексных амплитуд и имеют вид:

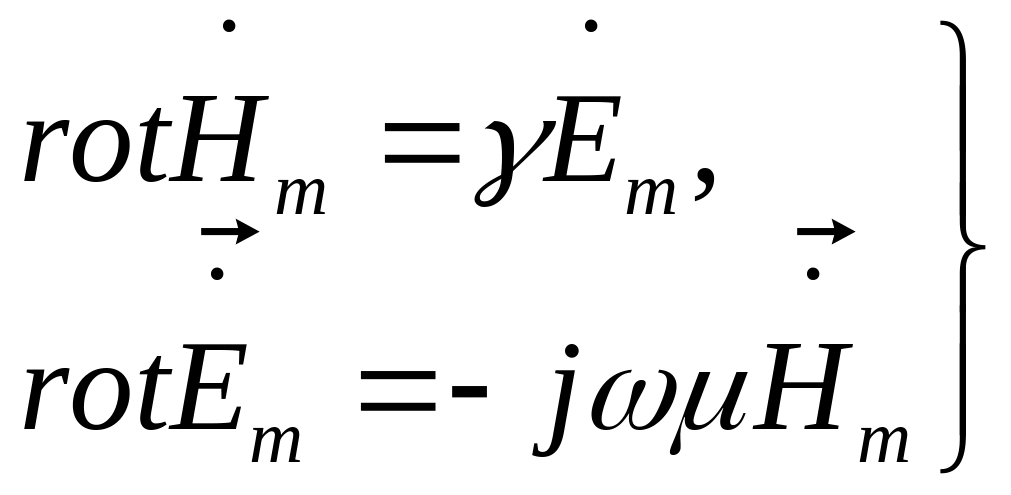(1)

В случае однородной среды система (1) сводиться к двум дифференциальным уравнениям второго порядка:

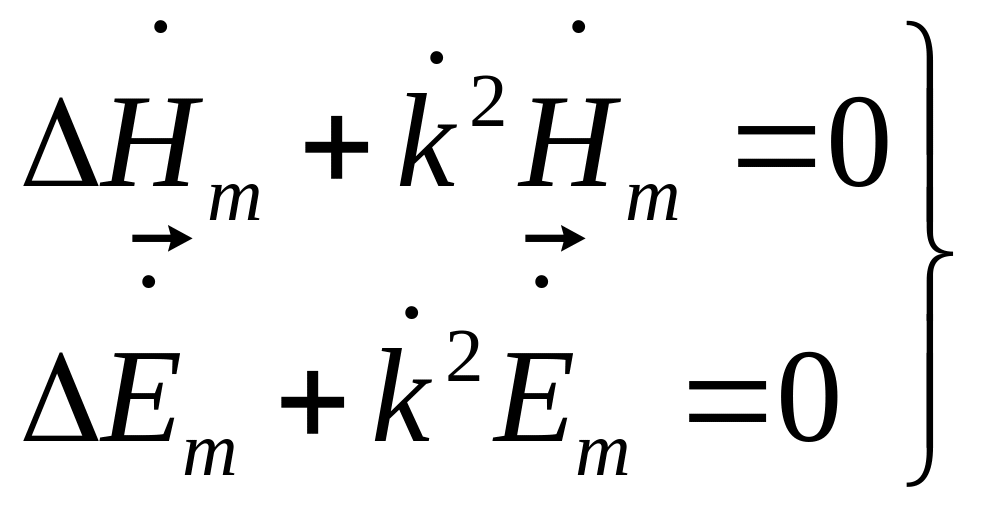(2)

где – комплексное волновое число;

α - постоянная затухания ;

β - постоянная распространения, .

При исследовании электромагнитного поля в проводнике полагаем, что оно туда проникает из внешней среды (рис.2). В проводнике происходит поглощение электромагнитной энергии, сопровождающееся выделением тепла. Если проводник занимает всё нижнее полупространство и вектор , где - единичный вектор вдоль оси X, то решение уравнения (2) для напряжённости электрического поля будет следующим:

Согласно последнему выражению амплитуда волны в направлении распространения поля экспоненциально убывает.

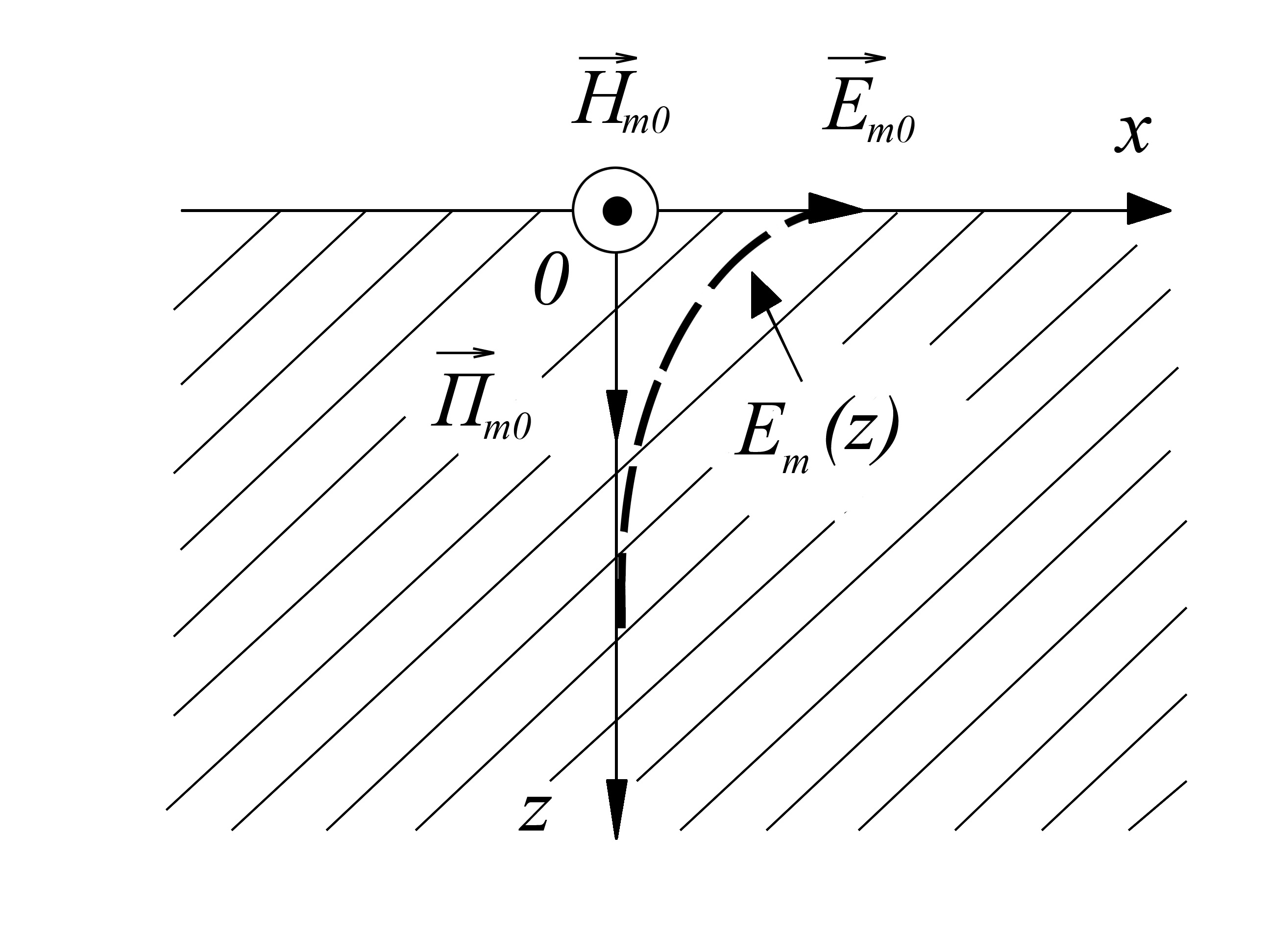
рис.2. Распределение напряжённости по сечению проводника

Параметр

называется глубиной проникновения. Это расстояние вдоль распространения волны, на котором амплитуда напряженности электрического поля уменьшается в раз, а явление неравномерного распределения поля вдоль направления распространения в проводнике, при котором амплитуды напряжённостей электрического и магнитного полей на его поверхности достигают максимального значения, называют поверхностным эффектом.

Различают электрический и магнитный поверхностные эффекты. В первом случае вектор напряжённости магнитного поля направлен вдоль проводника. Наблюдается затухание вектора в направлении от поверхности к центру проводника. При магнитном поверхностном эффекте вектор напряжённости магнитного направлен вдоль проводника и имеет место затухание вектора в направлении от поверхности к центру проводника.

Определяют вид поверхностного эффекта по степени его выраженности. Для этого сравниваем поперечный радиус для проводника круглого сечения или величину половины толщены (а) для плоской шины с величиной параметра глубины проникновения .Возможны три случая:

1) -поверхностный эффект практически отсутствует и считаем, что величина вектора постоянна в любой точке поперечного сечения проводника при электрическом поверхностном эффекте (такое допущение справедливо и для вектора при магнитном поверхностном эффекте). Расчёт величины вектора осуществляется с помощью первого уравнения Максвелла в интегральной форме (4) при электрическом поверхностном эффекте (при магнитном поверхностном эффекте при определении величины вектора применяют второе уравнение Максвелла (5)):

(4)

(5)

2) - случай нерезко выраженного поверхностного эффекта.

3) - случай резко выраженного поверхностного эффекта.