8.7. Похідні обернених тригонометричних функцій.

За допомогою теоремою 8.11 отримаємо формули для похідних від обернених тригонометричних функцій.

Теорема 8.12. Якщо , то

.

Доведення. Використаємо формулу (8.3). У нас прямою функцією є функція , а оберненою до неї . Тому

і

або, якщо перейти до змінної х,

.

Таким чином,

Теорема 8.13. Якщо , то

.

Доведення. Аналогічно попередній теоремі маємо

і ,

тому

або

.

Тобто

Теорема 8.14. Якщо , то

.

Доведення. Оберненою до функції є функція . Тому і за формулою (8.3) отримуємо або, якщо перейти до змінної х ,

Теорема 8.15. Якщо , то

.

Доведення. Аналогічно попередній теоремі маємо

;

.

Приклад 8.7. Знайти похідну функції .

Розв’язування:

.

Тут використали теорему про похідну від складної функції: спочатку беремо похідну від степеневої функції u², де u=arcsin3x, далі від оберненої тригонометричної – , де , і в кінці – від 3х.

Приклад 8.8. Знайти похідну функції .

Розв’язування.

.

8.8. Таблиця похідних.

Всі отримані формули диференціювання зведемо в одну таблицю.

8.9. Похідна функції, заданої параметрично.

Розглянемо два рівняння

(8.5)

де t набуває значення на відрізку [t₀, t₁]. Кожному значенню аргументу t відповідають конкретні значення змінних х і у. Змінюючи t, будемо отримувати різні пари (х, у), сукупність яких можна розглядати як таблично задану функцію у з аргументом х. Якщо ж функція має обернену функцію , то після підстановки останньої в функцію отримаємо функцію (8.5) в явному вигляді .

Таким чином, пару функцій (8.5) можна розглядати як функцію у аргументу х за допомогою проміжного аргументу t, який ми називатимемо параметром, а саму функцію – параметрично заданою функцією.

Наведемо кілька прикладів параметрично заданих функцій.

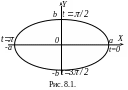
Приклад 8.9. Еліпс. Розглянемо рівняння

(8.6)

Ця система рівнянь задає в декартовій прямокутній системі координат ОХУ лінію, яка називається еліпсом (рис. 8.1).

Функцію (8.6) можна перевести в функцію, задану неявно. Дійсно, якщо перше рівняння розділити на а, а друге – на b; отримані рівняння піднести до квадрату і скласти, то дістанемо

або

.

Остання формула є канонічним рівнянням еліпса з центром у початку координат і півосями а і b. Таким чином, система (8.6) є параметричним заданням еліпса.

Приклад 8.10. Циклоїда.

Означення. 8.1 Циклоїдою називається лінія, яка описується точкою, що лежить на колі, яке котиться без ковзання по прямій (рис. 8.2).

Ц ю криву можна описати системою рівнянь:

де а – радіус кола.

Значення параметра t в точках на осі ОХ дорівнює , де

Перейдемо до обчислення похідної від функції заданої параметрично. Нехай задана системою (8.5). Припустимо, що для функцій існує похідна по змінній t і функція має обернену функцію , яка також має похідну, але по змінній х. Тоді задану параметрично функцію можна розглядати як складну функцію , . Змінна t грає роль проміжного аргументу.

За теоремою 8.7 отримуємо

.

Але за теоремою 8.11 виходить, що , і, таким чином,

або .

Остання формула дає змогу обчислювати похідну функції, заданої параметрично, не переводячи її в неявно або явно заданий вигляд.

Приклад 8.11. Знайти похідну функції

Розв’язування.

.

Приклад 8.12. Знайти значення похідної для функції

при t=2.

Розв’язування. Спочатку знайдемо похідну в загальному вигляді

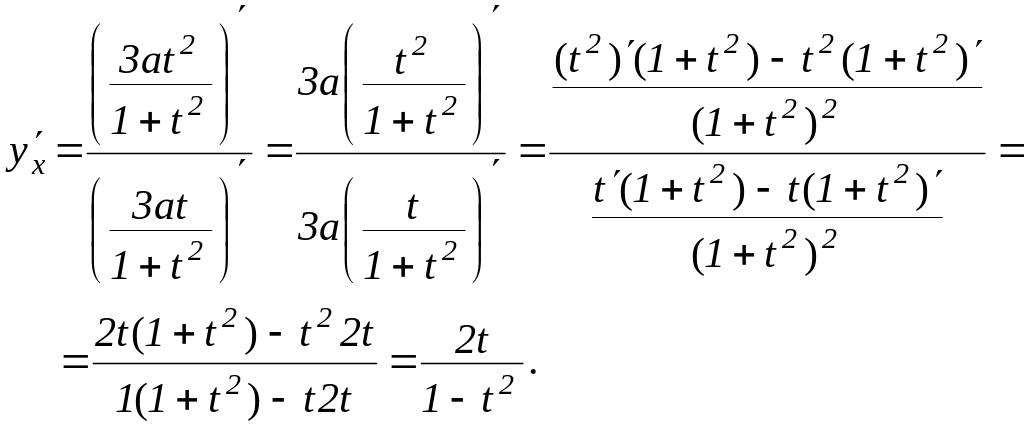
Тепер знайдемо значення останнього виразу при t=2:

.

Запитання для самоконтролю.

1. Виведіть формули для похідних функцій , .

2. Виведіть формули для похідних функцій , .

3. Чому дорівнює похідна від логарифмічної функції ?

4. Як співвідносяться похідні функцій і ?

5. Яка функція називається складною?

6. Виведіть правило диференціювання складної функції.

7. Як обчислюється похідна функції, заданої неявно?

8. Сформулюйте і виведіть теорему про похідну від степеневої функції.

9. Як обчислюється похідна показникової функції?

10. Запишіть формулу для похідної функції .

11. Сформулюйте поняття оберненої функції. В якому випадку вона існує?

12.Виведіть правило диференціювання оберненої функції.

13. Чому рівні похідні від обернених тригонометричних функцій?

14. Запишіть таблицю похідних.

15. Наведіть приклади параметрично заданої функцій.

16. Як диференціюється функція задана параметрично?

Приклади до розділу 8.

1. Знайти похідну функції:

а) . Відп.: .

2. Знайти похідну функції:

3. Продиференціювати функції:

4. Продиференціювати функції:

5. Знайти похідні функцій, заданих неявно і параметрично:

а)