Розділ 8. ПОХІДНІ ОСНОВНИХ ЕЛЕМЕНТАРНИХ

Функцій.

8.1. Похідна від тригонометричних функцій.

Теорема 8.1. Якщо , то .

Доведення. Дамо аргументові х приріст . Тоді можна записати

.

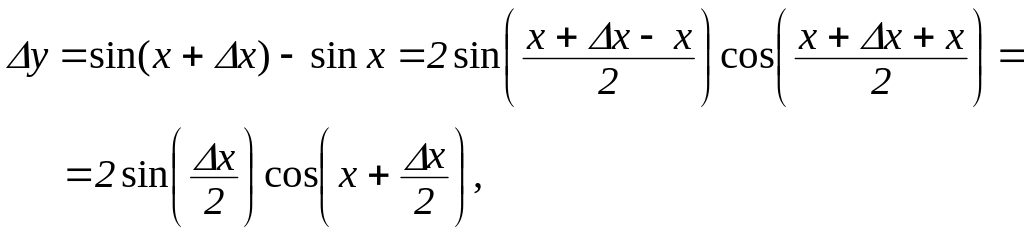
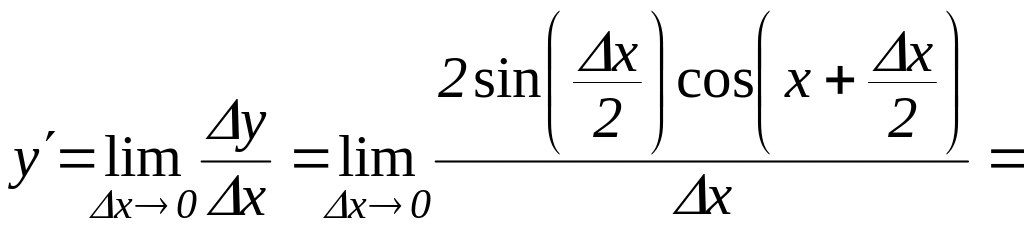
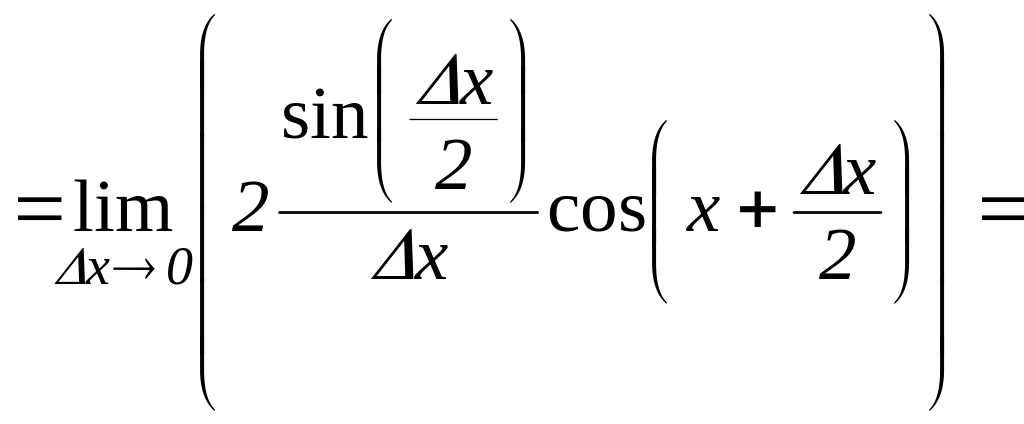
Обчислюючи дві останні границі, ми використали першу “чудову” границю і те, що функція неперервна.

Таким чином, cos x і теорему доведено

Теорема 8.2. Якщо , то .

Доведення. Аналогічно попередній теоремі маємо

,

,

,

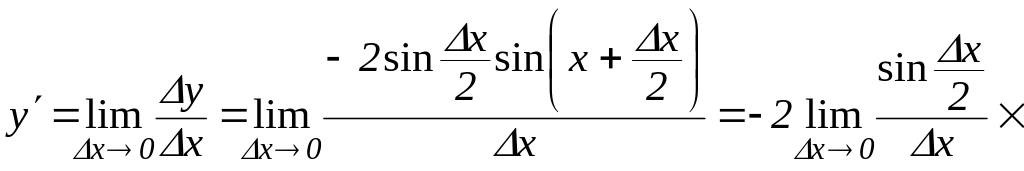
тобто

Теорема 8.3. Якщо , то .

Доведення. Використаємо теорему 7.4, тобто формулу про похідну від відношення двох функцій:

.

Таким чином,

Теорема 8.4. Якщо , то

Доведення. Аналогічно попередній теоремі отримуємо

,

таким чином

8.2. Похідна логарифмічної функції.

Теорема 8.5. Якщо , то .

Доведення. Надамо аргументові х приріст . Тоді

,

,

,

.

В останньому перетворенні ми використали неперервність функції . Введемо нову змінну . Очевидно, що при . Тоді з наслідку 4.2.2 до другої “чудової” границі, де і можна записати:

Наслідок. 8.5. Якщо , то

Дійсно, при а=е маємо

Теорема 8.6. Якщо , то .

Доведення. а) Якщо x>0, то і , тому ;

б) Нехай x<0, тоді і . Зауважимо, що при x<0. Таким чином, для функції одержуємо

;

.

Далі аналогічно доведенню теореми 8.5 дістаємо

.

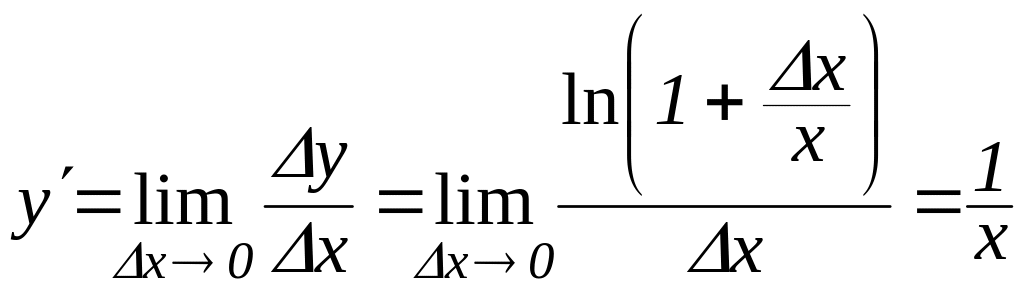Таким чином, для від’ємних значень х також справджується рівність , тобто теорему доведено для будь-яких . При х=0 функція невизначена

8.3. Похідна складної функції.

Розглянемо складну функцію , тобто функцію, яку можна подати у вигляді: де ; або Тут , – відповідно внутрішня і зовнішня функція, u – проміжний аргумент.

Виведемо правило диференціювання складної функції.

Теорема 8.7. Якщо функція має в деякій точці х похідну , а функція має за відповідного значення похідну , то складна функція в точці х має похідну .

Іншими словами, похідна складної функції дорівнює добутку похідної зовнішньої функції по проміжному аргументу на похідну проміжного аргументу по незалежній змінній.

Після обчислення похідної в останній вираз замість u потрібно підставити функцію .

Доведення. Для значень аргументу х і маємо

тобто приросту відповідає приріст , якому в свою чергу відповідає приріст . Зауважимо, що при вирази і теж прямують до нуля, так як і диференційовані функції

За умовою теореми

.

Тому за теоремою 3.1 можна записати:

або ,

де при . Розділимо обидві частини останньої рівності на і перейдемо до границі при :

Таким чином, і теорему доведено

Приклад 8.1. Знайти похідну функції .

Розв’язування. Запишемо задану функцію у вигляді , де . Тоді за теоремою 8.7 отримаємо

.

Приклад 8.2. Знайти похідну функції .

Розв’язування. Аналогічно попередньому прикладу маємо ( ):

.

8.4. Похідна функції, заданої неявно.

Нехай залежність між двома змінними х і у задана деяким рівнянням, яке символічно можна записати у вигляді

. (8.1)

Розглянемо функцію , визначену в деякому інтервалі . Якщо рівняння (8.1) при підстановці в ньому замість змінної у виразу перетворюється в тотожність, то воно є неявним заданням функції і його інколи записують у вигляді

.

Наприклад: 1) ; 2) .

В першому прикладі можна перейти від неявно заданої функції до явно заданої: .

Покажемо на прикладі як обчислюється похідна від функції заданої неявно.

Нехай задана функція , де , тобто .

Продиференціюємо останню рівність, враховуючи, що cos(y(x)+x) складна функція:

або

.

З останньої рівності виражаємо похідну :

або

.