Chapter 1. Multiple Integrals.

1.1. Some examples leading to the notion of a multiple integral.

Let us consider a solid (Ω) with the density of mass distribution .The density  can be variable that is different at different points of the solid. Let the function = (M) (where M is a point of Ω) be known and let it be necessary to determine the whole mass m of the solid.

Let us mentally divide the solid (Ω) into n parts (subregions) (Ω_k), k=1,2,….,n , denote as ∆Ω_k as the volume of (Ω_k) then choose arbitrary points M_k , k=1,2,….,n in each of the subregions (Ω_k). If the parts (Ω_k) are sufficiently small we can regard the density as being constant within each of the parts without an essential error. Then the mass m_(∆Ωk) of the part (Ω_k) can be computed as the product of the density by the volume.

Thus we obtain

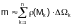
This is an approximate equality since the densities of the parts are nevertheless variable. But the smaller parts the greater accuracy. Hence, passing to the limit, as ∆Ω_k → 0, we obtain the exact equality.

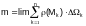
The limit is taken here in a process in which not only the volumes but also all the linear sizes of the parts tend to zero. Besides, it is supposed that the limit does not depend on the way of the partitioning (Ω) into subregions.

Reasoning in similar way we can conclude that if an electric charge is distributed over a solid (Ω) with density σ the magnitude q of the charge is found by means of the formula

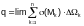
1.2. Definition and basic properties

For definiteness, let us consider integrals over three- dimensional regions. Suppose we are given a bounded (finite) region (Ω) in space. Let a function u=f (Ω) be defined over (Ω) and let the value f (Ω) of the function be finite at each point M of the region. To compose an integral sum we arbitrarily break up the region (Ω) into subregions (Ω₁), (Ω₂), …, (Ω_n) and take an arbitrary point. M_k (k=1, 2,…., n) in each of them. Then we write down integral sum:

,

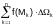where ∆Ω_k denotes the volume of the subregion (Ω_k).

The limit of the integral sum taken in a process in which all the linear sizes of the subregions entering into the partitions of the region (Ω) are unlimitedly decreased is called the integral of the function f over region (Ω). Denoting the integral be the symbol 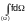we can write

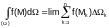
(Ω) is called the region (domain) of integration. Compare this with the basic definition of the definite integral.

The basic properties of a definite integral are implied be the definition of an integral as the limit of the integral sum. Therefore we can easily extend these properties to multiple integrals.

We enumerate them here.

1. The integral of sum equals the sum of the integrals of the summands (the same is true for the difference):

.

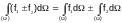2. A constant factor can be taken outside the sign of integration:

.

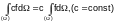3. The theorem of a partition of the region of integration: for any partition of region (Ω) into parts the integral over the whole region is equal to the sum of the integrals over the parts. For definiteness, if (Ω) is divided into the parts (Ω₁) and (Ω₂) we have:

.

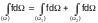4. The integral if unity is equal to the measure of the region of integration

.

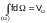5. It is allowable to integrate inequalities:

if f ₁≤f₂ .

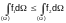6. An integral satisfies the inequalities:

.

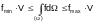7. They are connected with notion other of the mean value ƒ of a function ƒ over a region (Ω).

.

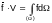8. There is an inequality of the form

.
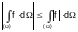