6. Обращение матриц

Операция обращения матриц применима только к квадратным матрицам (т.е. к матрицам, у которых количество строк равно количеству столбцов). Одна­ко не для каждой квадратной матрицы существует обратная к ней матрица. Что­бы матрицу можно было обратить, она должна быть несингулярной.

Опишем процедуру обращения несингулярной квадратной матрицы с помощью функции массива МОБР( ).

1. Введите матрицу, которую нужно обратить.

2. Укажите место для размещения обратной матрицы и ее правильный размер (он совпадает с размером исходной матрицы).

3. Начните вводить функцию массива МОБР(матрица) и укажите с помощью мыши ячейки, в которых содержится обращаемая матрица. Завершите формулу вводом закрывающей скобки.

4. Нажмите комбинацию клавиш Ctrl+Shift+Enter , чтобы ввести матричную функцию во все ячейки, отмеченные при выборе расположения результирующей матрицы.

Задание: Выполните операцию обращения матрицы

А =

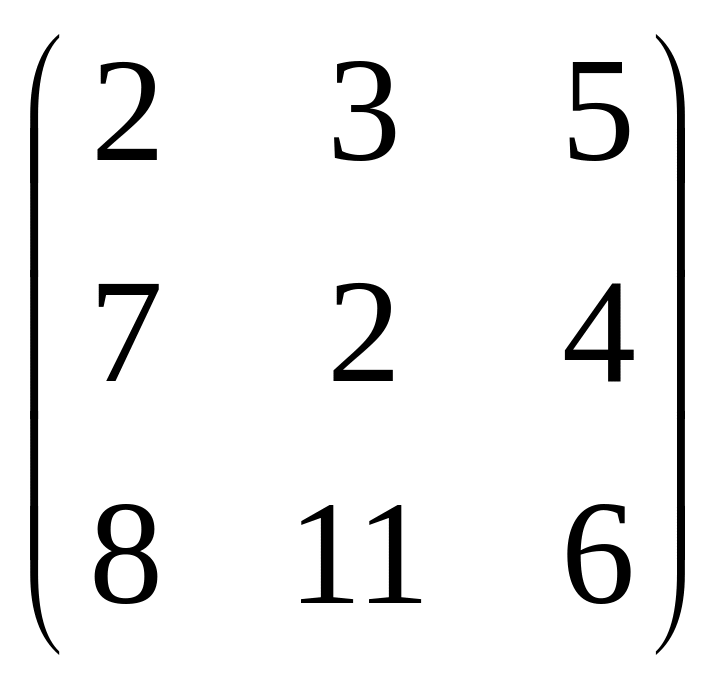
7. Примеры решения задач

1. Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки F1:G2, а свободные члены – в ячейки I1:I2 (рис. 30). Для решения этой задачи вспомним, что решение линейной системы АХ=В, где А – матрица коэффициентов, В – столбец (вектор) свободных членов, Х – столбец (вектор) неизвестных, имеет вид Х=А^-1В, где А^-1 – матрица, обратная по отношению к матрице А. Поэтому для решения нашей системы уравнений выделим под вектор решений диапазон К1:К2 и введем в него формулу, как показано на рис. 30.

Рис. 30. Решение системы линейных уравнений

 

2. Решим также систему линейных уравнений А²Х=В, где

, .

Для решения этой системы введем в диапазон ячеек А1:В2 элементы матрицы А, а в диапазон ячейки D1:D2 – элементы столбца свободных членов В. Выберем диапазон F1:F2, куда поместим элементы вектора решения, и введем следующую формулу:

{=МУМНОЖ(МОБР(МУМНОЖ(А1:В2;А1:В2));D1:D2)}

3. Рассмотрим пример вычисления квадратичной формулы z=X^TAX, где А – квадратная матрица, введенная в диапазон А1:В2, Х – вектор, введенный в диапазон D1:D2, а символ (^Т) обозначает операцию транспонирования. Для вычисления z введем в ячейку F1 (рис. 31) формулу:

{=МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);A1:B2);D1:D2)}

 

Рис. 31. Нахождение квадратичной формы

 

Хотя результатом этой формулы является число, не забудьте для ее ввода нажать клавиши Ctrl+Shift+Enter. Если этого не сделать, в ячейке F1 появится сообщение #ЗНАЧ!

4. Вычислим теперь значение квадратичной формы z=Y^TA^TAY, где

, Y= .

Для решения этой задачи введем в диапазон ячеек А1:В2 элементы матрицы А, а в диапазон D1:D2 – элементы столбца Y. Для вычисления квадратичной формы введем в ячейку F1 формулу:

{=МУМНОЖ(ТРАНСП(D1:D2);МУМНОЖ(ТРАНСП(А1:В2);МУМНОЖ(А1:В2;D1:D2)))}.

8. Решение системы линейных уравнений методом Гаусса

В качестве следующего примера работы с массивами рассмотрим решение системы линейных уравнений методом Гаусса. На рис. 32. приведены результаты решения методом Гаусса следующей системы линейных уравнений:

2х₁+3х₂+7х₃+6х₄=1,

3х₁+5х₂+3х₃+х₄ =3,

5х₁+3х₂+х₃+3х₄ =4,

3х₁+3х₂+х₃+6х₄ =5.

  В диапазоны ячеек А33:D36 и Е33:Е36 введены матрица коэффициентов и столбец свободных членов, соответственно. Содержимое ячеек А33:Е33 скопировано в ячейки А38:Е38, А43:Е43 и А48:Е48. В диапазон ячеек А39:Е39 введена формула:

{=A34:E34-$A$33:$E$33*(A34/$A$33)},

 обращающая в нуль коэффициент при х₁ во втором уравнении системы.

Рис. 32. Пошаговое решение системы линейных уравнений методом Гаусса

Выделим диапазон А39:Е39 и протащим маркер выполнения этого диапазона так, чтобы выполнить диапазон А39:Е41. Это обратит в нуль коэффициент при х₁ в третьем и четвертом уравнениях системы. Скопируем значения из диапазона ячеек А39:Е39 в диапазоны А44:Е44 и А49:Е49. Для копирования значений без формул воспользуйтесь командой Правка, Специальная вставка и в открывшемся диалоговом окне Специальная вставка в группе Вставить установите переключатель в положение Значение.

  В диапазон ячеек А45:Е45 вводим формулу:

{=A40:E40-$A$39:$E$39*(B40/$B$39)}.

Выделим диапазон А45:Е45 и протащим маркер заполнения этого диапазона так, чтобы заполнить диапазон А45:Е46. Это обратит в нуль коэффициент при х₂ в третьем и четвертом уравнениях системы. Копируем значения из диапазона ячеек А45:Е45 в диапазон А50:Е50. В диапазон ячеек А51:Е51 вводим формулу

{=A46:E46-$A$45:$E$45*(C46/$C$45)},

которая обращает в нуль коэффициент при х₃ четвертого уравнения системы. Прямая прогонка метода Гаусса завершена. Обратная прогонка заключается в вводе в диапазоны G36:К36, G35:K35, G34:K34 и G33:K33, соответственно, следующих формул:

{=A51:E51/D51}

{=(A50:E50-G36:K36*D50)/C50}

{=(A49:E49-G36:K36*D49-G35:K35*C49)/B49}

{=(A48:E48-G36:K36*D48-G35:K35*C48-G34:K34*B48)/A48}

В диапазоне ячеек К33:К36 получено решение системы.