2.7. Цепь синусоидального тока с последовательным соединением r, l, c – элементов. Резонанс напряжений

В общем случае любое реальное устройство, содержащееся в электрической цепи, может быть представлено в схеме замещения тремя идеальными элементами. Поэтому целесообразно при анализе цепей синусоидального тока знать соотношение тока и напряжения для участка цепи с тремя последовательно соединенными элементами: резистором, идеальным индуктивным и идеальным емкостным элементами.

Схема замещения такой неразветвленной цепи показана на рис. 2.17.

Рис. 2.17. Схема цепи с последовательным соединением элемен­тов R, L, C.

Под действием синусоидального напряжения в цепи возникает синусоидальный ток i. Необходимо определить соотношение между синусоидальными током и напряжением этой цепи по величине и по фазе.

Синусоидальный ток с амплитудой I_m и начальной фазой ψ_i изображается в виде:

i = I_msin(ωt+ψ_i) , (2.98)

или в комплексной форме:

. (2.99)

По второму закону Кирхгофа для контура рассматриваемой цепи полное напряжение цепи соотносится с напряжениями на отдельных элементах в виде:

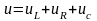или 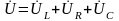(2.100)

Как показано ранее (51), (71), (90), напряжение на каждом из элементов соотносятся с током в соответствии с законом Ома:

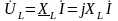, (2.101)

, (2.102)

. (2.103)

Ток во всех элементах при их последовательном соединении один и тот же. Тогда выражение (98) может быть представлено в виде:

(2.104)

Или . (2.105)

Здесь 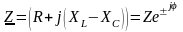(2.106)

- комплексное полное сопротивление цепи с тремя последовательно соединенными элементами.

Таким образом, выражение (2.105) определяет соотношение между комплексным током и комплексным напряжением также в форме закона Ома: комплексный ток в цепи с тремя последовательно соединенными элементами прямо пропорционален комплексному напряжению и обратно пропорционален комплексному полному сопротивлению этой цепи.

Модуль и аргумент комплексного полного сопротивления определяются параметрами отдельных элементов.

Исходя из (2.106) , модуль комплексного полного сопротивления

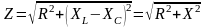, (2.107)

где – реактивное сопротивление цепи.

Аргумент комплексного полного сопротивления . (2.108)

В соответствии с законом Ома в комплексном виде для этой цепи (2.105) ,

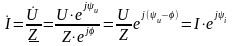. (2.109)

Исходя из полученного выражения (2.109) , действующее значение тока

, (2.110)

начальная фаза тока

, или . (2.111)

Как видно, действующие значения тока и напряжения в этой цепи также определяется полным сопротивлением Z в форме закона Ома. По фазе напряжение опережает ток на угол φ. При этом полное сопротивление и разность фаз определяются соотношением сопротивлений трех элементов в соответствии выражениями (2.107) и (2.108).

Тот же результат может быть получен посредством наглядного графического изображения тока и напряжений на векторной диаграмме.

Векторная диаграмма для рассматриваемой цепи показана на рис. 2.18.

Здесь начальная фаза тока принята произвольно равной нулю (ψ_i = 0). При этом вектор тока направлен вдоль вещественной оси комплексной плоскости.

Рис. 2.18. Векторная диаграмма цепи с последовательным соединением элементов L, R, C.

Вектор напряжения индуктивного элемента повернут относительно вектора тока на π/2 в сторону опережения в соответствии со свойствами этого элемента (2.55). Вектор напряжения резистора направлен вдоль вектора тока в соответствии со свойствами резистора (2.36). Вектор напряжения емкостного элемента повернут на угол π/2 относительно вектора тока в сторону отставания в соответствии со свойствами емкостного элемента (85). Длина векторов напряжений определяется их действующими значениями по закону Ома для каждого из элементов в соответствии с (2.56), (2.35), (2.72).

Соотношение напряжений по второму закону Кирхгофа (2.100) на векторной диаграмме соответствует векторному сложению. При этом вектор полного напряжения цепи на рис. 2.18 определяется суммой трех векторов напряжений на отдельных элементах:

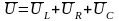(2.112)

Из построенной векторной диаграммы возможен анализ соотношения тока и полного напряжения цепи. Для этого выделим на векторной диаграмме прямоугольный треугольник ОАВ (см. рис. 2.19).

Рис. 2.19. Треугольник напряжений цепи с последовательным соединением элементов.

Нижний катет треугольника пропорционален напряжению резистора, которое определяется его активным сопротивлением, и его называют активной составляющей напряжения (U_а=U_R). Правый катет треугольника пропорционален разности напряжений двух реактивных элементов: индуктивного и емкостного, и его называют реактивной составляющей напряжения:

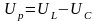. (2.113)

Гипотенуза треугольника пропорциональна величине полного напряжения цепи U. Угол φ определяет разность фаз всей цепи.

Этот треугольник называют треугольником напряжений и используют для наглядного представления соотношения между отдельными составляющими напряжений при анализе цепи с последовательным соединением R,L,C – элементов.

Поделим стороны треугольника напряжений на величину тока I. При этом получается подобный треугольник (см. рис. 2.20) со сторонами:

Рис. 2.20. Треугольник сопротивлений цепи с последовательным соединением элементов.

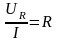- активное сопротивление резистора;

- реактивное сопротивление, определяемое разностью индуктивного и емкостного сопротивлений;

- полное сопротивление цепи, определяющее соотношение по величине тока и полного напряжения.

Угол φ определяет разность фаз всей цепи.

Этот треугольник называют треугольником сопротивлений и используют для наглядного представления соотношения между сопротивлениями отдельных элементов и полным сопротивлением цепи с последовательным соединением R,L,C – элементов.

По теореме Пифагора для треугольника сопротивлений модуль полного сопротивления

. (2.114)

Он определяет соотношение по величине между током и полным напряжением.

Из того же треугольника разность фаз для всей цепи

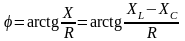. (2.115)

Она описывает соотношение по фазе между током и полным напряжением и определяет аргумент комплексного полного сопротивления.

Таким образом, комплексное полное сопротивление может быть записано в виде:

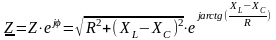. (2.116)

Оно определяет соотношение между током и напряжением по закону Ома в комплексном виде:

. (2.117)

При этом модуль комплексного полного сопротивления Z определяет соотношение по величине действующих значений напряжения и тока: 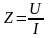, а аргумент комплексного сопротивления определяет соотношение синусоидальных напряжения и тока по фазе: .

Полученные при графическом анализе выражения (2.114) - (2.117) соответствуют записанным ранее (2.107) - (2.109).

Эти выражения справедливы для цепи, содержащей в общем случае три идеальных элемента, соединенные последовательно. В частности, реальное устройство может быть представлено в схеме замещения двумя или одним идеальным элементом. В этом случае полученные выражения также справедливы. Следует лишь формально принять сопротивление отсутствующего элемента равным нулю.

Используя графические изображения в форме треугольников напряжений и сопротивлений, можно записать выражения, полезные при расчете и анализе такой электрической цепи:

; (2.118)

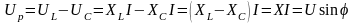; (2.119)

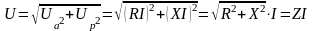; (2.120)

. (2.121)

Для анализа энергетических соотношений в цепи с последовательным соединением R, L, C – элементов определим характер изменения мгновенной мощности в этой цепи:

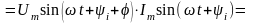
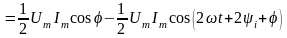. (2.122)

Или, используя действующие значения тока и напряжения,

. (2.123)

Как видно из полученного выражения (121), мощность в рассматриваемой цепи изменяется во времени по гармоническому закону с двойной частотой. При этом колебания мощности происходят вокруг среднего значения, определяемого первым слагаемым в правой части этого выражения.

Среднее значение мощности определяет активную мощность. Тогда активная мощность

. (2.124)

или

. (2.125)

Как видно, активная мощность определяется мощностью резистора.

Произведение действующих значений тока и полного напряжения цепи называют полной мощностью S:

. (2.126)

Единица полной мощности – ВА, кВА, МВА.

Исходя из (2.125 ) и (2.126) соотношение активной и полной мощностей:

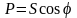, или 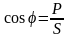. (2.127)

Активная мощность определяет необратимое преобразование электрической энергии в другие виды энергии, т.е. полезную работу, совершаемую током в электрической цепи. В общем случае активная мощность составляет лишь часть полной мощности, определяемой произведением действующих значений тока и полного напряжения. Эта доля активной мощности в полной определяется выражением (2.127). Отношение активной мощности к полной называется коэффициентом мощности. Принимая во внимание выражение (2.127), коэффициент мощности обозначают cosφ.

Коэффициент мощности можно определить соотношением сопротивлений отдельных элементов, например, исходя из треугольника сопротивлений (рис. 2.20):

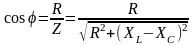. (2.128)

Графически соотношение активной и полной мощности отображается треугольником мощностей. Для построения треугольника мощностей умножим треугольник напряжений на действующее значение тока. При этом образуется подобный прямоугольный треугольник (см. рис. 2.21) .

Рис. 2.21. Треугольник мощностей цепи с последовательным соединением элементов

Нижний катет треугольника пропорционален активной мощности:

. (2.129)

Правый катет треугольника пропорционален величине:

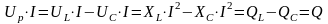. (2.130)

Это реактивная мощность всей цепи.

Гипотенуза треугольника оказывается равной полной мощности:

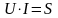. (2.131)

Из треугольника мощностей:

, (2.132)

, (2.133)

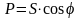, или , (2.134)

Что соответствует полученным ранее выражениям.

При выполнении расчетов в комплексном виде комплексное значение полной мощности определяется произведением комплексного напряжения на сопряженный комплексный ток:

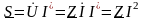. (2.135)

Здесь 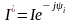сопряженный комплексный ток. Тогда:

2.136)

В рассматриваемой цепи с последовательным соединением R, L, C – элементов при разном соотношении сопротивлений элементов (R, X_L, X_C) создается разный режим работы. При этом характер цепи определяется разностью фаз φ, значения которой могут быть положительными или отрицательными в диапазоне от π/2 до – π/2 .

Ниже рассматриваются режимы работы цепи при разных соотношениях индуктивного и емкостного сопротивлений.

Показанная на рис. 2.18 векторная диаграмма построена в предположении, что индуктивное сопротивление больше емкостного (Х_L > Х_C ). Реактивное сопротивление всей цепи положительно:

. (2.137)

При этом в соответствии с законом Ома напряжение на индуктивном элементе больше емкостного:

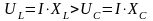. (2.138)

Разность фаз всей цепи оказывается положительной, т.е. полное напряжение опережает по фазе ток на угол φ, больший нуля:

. (2.139)

Треугольник сопротивлений и треугольник мощностей для этого режима имеют вид, показанный на рис. 2.20, 2.21.

В этом режиме цепь характеризуется активной мощностью P и положительной реактивной мощностью Q>0. Положительное значение реактивной мощности свидетельствует о том, что индуктивная мощность больше емкостной, т.е. индуктивный элемент преобладает над емкостным элементом.

В этом режиме характер цепи называют активно–индуктивным.

При сопротивлении индуктивного элемента, меньшим емкостного, (Х_L < Х_C ) реактивное сопротивление всей цепи отрицательно:

(2.140)

При этом в соответствии с законом Ома напряжение на индуктивном элементе меньше емкостного:

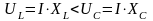. (2.141)

Векторная диаграмма для этого режима показана на рис. 2.22.

Рис. 2.22. Векторная диаграмма неразветвленной цепи при Х_L < Х_C.

Разность фаз всей цепи оказывается отрицательной, т.е. полное напряжение отстает по фазе от тока:

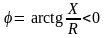. (2.142)

Треугольник сопротивлений и треугольник мощностей для этого режима показаны на рис. 2.23.

Рис. 2.23. Треугольник сопротивлений и треугольник мощностей

при Х_L < Х_C

В этом режиме цепь характеризуется активной мощностью P и отрицательной реактивной мощностью Q<0. Отрицательное значение реактивной мощности свидетельствует о том, что индуктивная мощность меньше емкостной, т.е. емкостный элемент преобладает над индуктивным элементом.

В этом режиме характер цепи называют активно–емкостным.

Особый режим работы цепи возникает при равенстве индуктивного и емкостного сопротивлений:

Х_L = Х_C . (2.143)

Реактивное сопротивление всей цепи оказывается равным нулю:

(2.144)

При этом в соответствии с законом Ома напряжения на индуктивном и емкостном элементах равны между собой:

, (2.145)

а реактивное напряжение равно нулю:

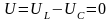(2.146)

Векторная диаграмма для этого режима показана на рис. 2.24.

Рис. 2.24. Векторная диаграмма неразветвленной цепи при Х_L = Х_C

Разность фаз всей цепи оказывается равной нулю, т.е. полное напряжение совпадает по фазе с током:

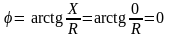. (2.147)

Треугольник сопротивлений и треугольник мощностей для этого режима вырождаются в отрезок, поскольку один катет становится равным нулю.

В этом режиме цепь характеризуется активной мощностью P . Реактивная мощность равна нулю Q = 0. При этом активная мощность равна полной мощности:

P = S = UI, (2.148)

а коэффициент мощности равен

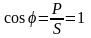. (2.149)

Отсутствие реактивной мощности при наличии в цепи индуктивного и емкостного элементов свидетельствует о том, что реактивная индуктивная мощность и реактивная емкостная мощность взаимно компенсируются. При этом цепь имеет активный характер, поскольку обладает лишь активной мощностью.

Явление, возникающее в неразветвленной цепи с элементами L, R, C, когда полное напряжение и ток совпадают по фазе, называется резонансом напряжений.

Условие резонанса напряжений:

Х_L = Х_C (2.150)

или . (2.151)

Создать резонанс напряжений в цепи можно изменяя параметры L или С при неизменной частоте, или изменяя частоту при заданных параметрах L и С.

Рассмотрим случай, когда L и С неизменны при изменении частоты. На рис. 2.25 показаны зависимости сопротивлений R, Х_L , Х_C, Z и тока цепи I от частоты f.

Рис. 2.25. Зависимости R, Х_L , Х_C, Z, I от частоты

В точке A Х_L = Х_C. При этом полное сопротивление минимально и определяется лишь активным сопротивлением резистора:

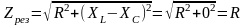. (2.152)

Эта точка определяет резонансную частоту 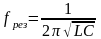. (2.153)

Ток цепи в этом режиме наибольший:

. (2.154)

Активная мощность определяется величиной резонансного тока:

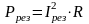. (2.155)

Аналогичным образом возникает режим резонанс напряжений при неизменной частоте и изменении индуктивности индуктивного элемента, либо емкости емкостного элемента. При установлении равенства индуктивного и емкостного сопротивлений возникает резонанс напряжений. При этом полное сопротивление цепи минимально, а ток максимальный.

Признаком резонанса напряжений в цепи является максимальное значение тока и активной мощности

Резонанс напряжений используется в радиотехнических цепях при построении схем резонансных фильтров. При этом свойства цепи оказываются различными для сигналов разных частот.

В электротехнических установках частота неизменна. Здесь возникновение резонанса напряжений обусловлено изменением параметров элементов. При Х_L = X_C >R при резонансе напряжений возможны перенапряжения на отдельных участках цепи.