Методические указания к заданию 5
1. Определить относительную погрешность измерения напряжения Uх каждым прибором используя формулы:
,
,
.
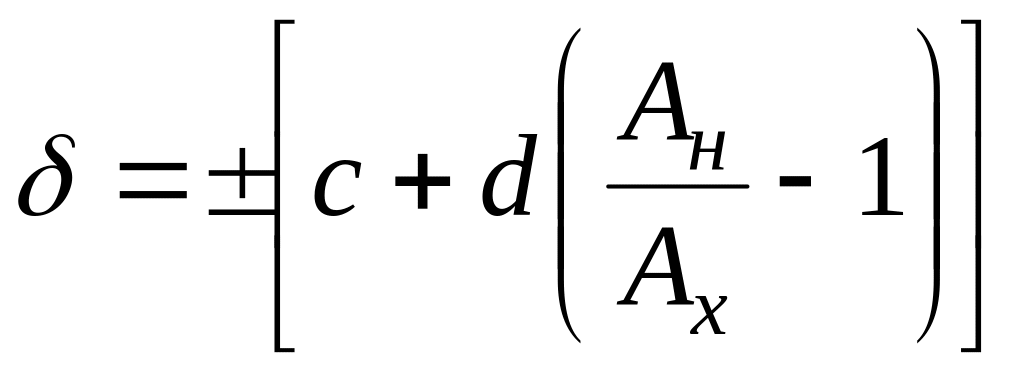2. Сравнить полученные значения с заданным δx и сделать выбор.
Задание 6
Проводят измерение параметра электрической
цепи. Определить вероятность попадания
случайной погрешности в симметричный
интервал с границами от -
до +
для нормального закона распределения,
если известно среднее квадратическое
отклонение погрешности
.
Исходные данные для расчета представлены
в табл.8.
Табл. 8
Параметр |
Вариант (последняя цифра шифра) |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
|
122 |
0,5 |
30 |
1860 |
0,07 |
56 |
760 |
10 |
80 |
150 |
1 |
380 |
0,9 |
46 |
2520 |
0,20 |
160 |
2500 |
8 |
150 |
250 |
Методические указания к заданию 6
Вероятность попадания случайной
погрешности в интервал от -
до +
определяется по формуле:
. (2)
Функция плотности распределения погрешности (плотность вероятности) для нормального закона описывается выражением:
.
(3)
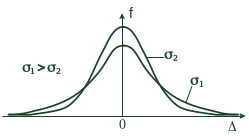
Чем больше ,
тем более полога кривая
,
т.е. увеличивается рассеивание результатов
измерений.
Подставим (3) в (2) и примем, что -
= +
,
получим вероятность попадания случайной
погрешности в симметричный интервал
от -
до +
:
(3)
Для удобства вычисления интеграла
функцию
нормируют, заменяя переменную
на переменную
:
.
Функцию
называют плотностью стандартного
нормального распределения.
Плотность
связана с плотностью
соотношением
.
Интеграл от
называют функцией Лапласа или
интегралом вероятности
:
.
Функция
определяет вероятность попадания в
интервал
,
следовательно, вероятность попадания
в интервал
равна удвоенному значению
,
т.е.
.
Значения
(или
)
табулированы для разных значений z.
Для нахождения вероятности нужно сначала рассчитать z, затем по таблице определить , которая и будет определять вероятность попадания в симметричный интервал . Значения функций и табулированы для разных значений z в табл. 9.
Табл. 9
Таблица значений функции Лапласа
z |
|
|
z |
|
|
z |
|
|
0 |
0 |
0 |
1,25 |
0,39435 |
0,78870 |
2,50 |
0,49379 |
0,98758 |
0,05 |
0,01994 |
0,03988 |
1,30 |
0,40320 |
0,80640 |
2,55 |
0,49461 |
0,98922 |
0,10 |
0,03983 |
0,07966 |
1,35 |
0,41149 |
0,82298 |
2,60 |
0,49535 |
0,99069 |
0,15 |
0,05962 |
0,11924 |
1,40 |
0,41925 |
0,83849 |
2,65 |
0,49598 |
0,99195 |
0,20 |
0,07926 |
0,15852 |
1,45 |
0,42647 |
0,85294 |
2,70 |
0,49654 |
0,99307 |
0,25 |
0,09871 |
0,19741 |
1,50 |
0,43318 |
0,86635 |
2,75 |
0,49702 |
0,99404 |
0,30 |
0,11791 |
0,23582 |
1,55 |
0,43943 |
0,87886 |
2,80 |
0,49745 |
0,99489 |
0,35 |
0,13683 |
0,27366 |
1,60 |
0,44520 |
0,89040 |
2,85 |
0,49782 |
0,99563 |
0,40 |
0,15542 |
0,31084 |
1,65 |
0,45053 |
0,90106 |
2,90 |
0,49814 |
0,99627 |
0,45 |
0,17365 |
0,34729 |
1,70 |
0,45544 |
0,91087 |
2,95 |
0,49841 |
0,99682 |
0,50 |
0,19146 |
0,38292 |
1,75 |
0,45994 |
0,91988 |
3,0 |
0,49865 |
0,99730 |
0,55 |
0,20884 |
0,41768 |
1,80 |
0,46407 |
0,92814 |
3,1 |
0,49903 |
0,99806 |
0,60 |
0,27075 |
0,45150 |
1,85 |
0,46785 |
0,93569 |
3,2 |
0,49932 |
0,99863 |
0,65 |
0,24216 |
0,48431 |
1,90 |
0,47129 |
0,94257 |
3,3 |
0,49952 |
0,99903 |
0,70 |
0,25804 |
0,51607 |
1,95 |
0,47441 |
0,94882 |
3,4 |
0,49967 |
0,99933 |
0,75 |
0,27338 |
0,54675 |
2,00 |
0,47725 |
0,95450 |
3,5 |
0,49977 |
0,99953 |
0,80 |
0,28815 |
0,57629 |
2,05 |
0,47982 |
0,95964 |
3,6 |
0,49984 |
0,99968 |
0,85 |
0,30234 |
0,60468 |
2,10 |
0,48214 |
0,96427 |
3,7 |
0,49989 |
0,99978 |
0,90 |
0,31594 |
0,63188 |
2,15 |
0,48422 |
0,96844 |
3,8 |
0,49993 |
0,99986 |
0,95 |
0,32895 |
0,65789 |
2,20 |
0,48610 |
0,97219 |
3,9 |
0,49995 |
0,99990 |
1,00 |
0,34135 |
0,68269 |
2,25 |
0,48778 |
0,97555 |
4,0 |
0,49997 |
0,99994 |
1,05 |
0,35314 |
0,70628 |
2,30 |
0,48928 |
0,97855 |
4,1 |
0,49998 |
0,99996 |
1,10 |
0,36434 |
0,72867 |
2,35 |
0,49062 |
0,98123 |
4,2 |
0,49999 |
0,99997 |
1,15 |
0,37493 |
0,74986 |
2,40 |
0,49180 |
0,98360 |
4,4 |
0,49999 |
0,99999 |
1,20 |
0,38493 |
0,76986 |
2,45 |
0,49286 |
0,98571 |
4,5 |
0,49999 |
0,99999 |