МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Кафедра физики и экологической теплофизики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ по физике

Механика и молекулярная физика

Под общей редакцией

профессора В.Т. Волова

Самара 2014

УДК 537

Методические указания к выполнению лабораторных работ по физике для студентов всех специальностей дневной и заочной форм обучения [Текст] / Составители: Волов В.Т., Волов Д.Б., Кольчугин Н.А., Михайлов В.А., Вилякина Е.В., Хохлова Н.Ю. - Самара: СамГУПС, 2014. – 10 с.

Утверждено на заседании кафедры " 2" сентября 2014г., протокол № 1.

Печатается по решению редакционно-издательского совета университета.

Содержит введение в измерительный практикум. Приведены краткие теоретические сведения, описания, методические указания, способы оценок погрешностей при выполнении лабораторных работ.

Составители: В.Т. Волов

Д.Б. Волов

Н.А. Кольчугин

В.А. Михайлов

Е.В. Вилякина

Н.Ю. Хохлова

Рецензенты:

д.ф.-м. н., профессор кафедры «Общая и теоретическая физика» Горохов А.В.,

к.ф.-м.н., доцент кафедры «Высшая математика» Кузнецов В.П.

Редактор: И.М. Егорова

Компьютерная верстка: Н.В. Чертыковцева

Подписано в печать Формат 64х90 1/16

Бумага писчая. Печать оперативная. Усл. п.л. 1,25

Тираж 250. Заказ №

© Самарский государственный университет путей сообщения, 2014

Лабораторная работа №4 маятник максвелла. Определение момента инерции тел и проверка закона сохранения энергии

Цель работы: изучение законов динамики поступательного и вращательного движений, закон сохранения механической энергии, измерение и теоретическое определение момента инерции системы тел на примере маятника Максвелла.

1. Теоретическое введение

Л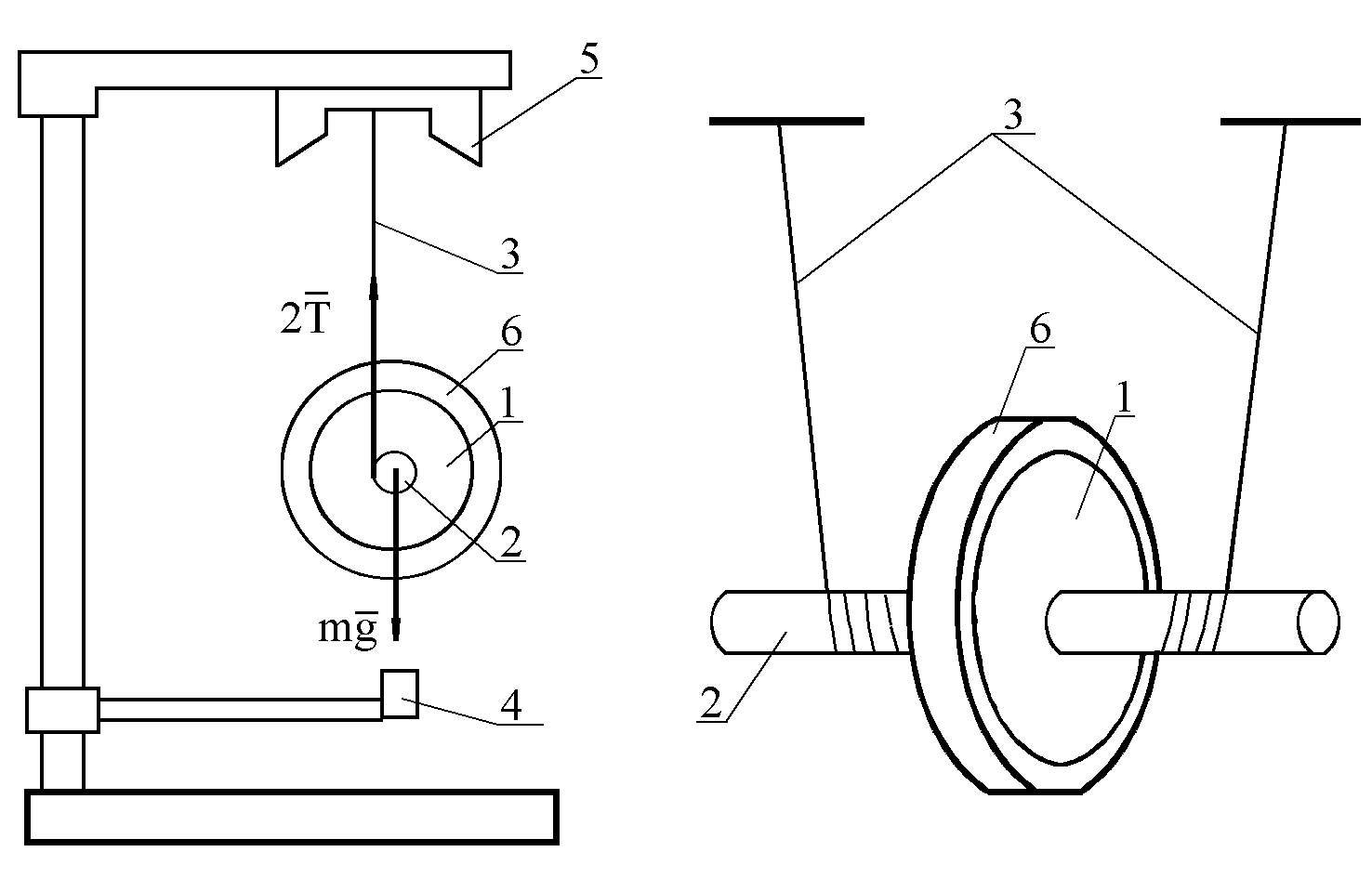 абораторная работа выполняется с использованием маятника Максвелла, который представляет собой небольшой диск, туго насаженный на ось и подвешенный на двух параллельных нитях – бифилярный подвес (рис.1).

Рис.1 Общий вид установки

Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен стержень 2. К концам этого стержня прикреплены две крепкие (капроновые) нити 3. Они наматываются на стержень (от концов его к диску). Фиксация диска маятника осуществляется при помощи электромагнита, входящего в устройство регулировки исходного положения 5. Фотодатчик 4 служит для остановки таймера. Диск маятника представляет собой непосредственно сам диск и сменные кольца 6, закрепляющиеся на диске.

Маятнику можно сообщить потенциальную энергию, подняв его на некоторую высоту, намотав при этом нити на ось. Маятник удерживается в верхнем положении электромагнитом. При выключении электромагнита силы и моменты силы, действующие на маятник, сообщают ему одновременно поступательное и вращательное движение.

Опустившись в крайнее нижнее положение, маятник будет по инерции вращаться в том же направлении, в результате нити намотаются на ось и маятник поднимается. Таким образом, происходит колебания маятника.

Поступательное движение маятника описывается вторым законом Ньютона, который без учета сил трения имеет вид:

,

где m – масса маятника, кг; а – ускорение поступательного движения центра масс маятника, м/с².

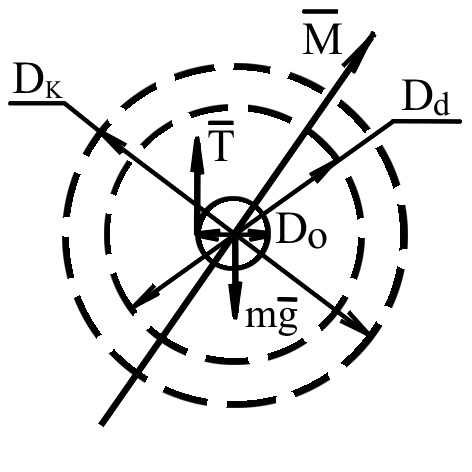
Рис.2

Проектируя это уравнение на направление ускорения , получим:

. (1)

Вращательное движение маятника описывается основным законом динамики вращательного движения для абсолютно твердого тела:

,

где J – момент инерции маятника относительно его оси вращения, кгм²;  - угловое ускорение, рад/с²; М – суммарный момент внешних сил относительно оси вращения, Нм.

Проектируя последнее уравнение на направление вектора (см. рис.2) и учитывая, что момент силы тяжести относительно оси вращения равен нулю, получим:

(2)

Момент сил натяжения нитей равен: , где r_о – радиус оси маятника Максвелла (плечо силы Т) и уравнение (2) принимает вид:

. (3)

Учитывая связь линейного и углового ускорения и того, что нет проскальзывания нити , из уравнений (1) и (3) получим выражение для момента инерции маятника Максвелла:

, ,

,

. (4)

Ускорение а может быть получено по измеренному времени движения t, за которое маятник совершает перемещение h из крайнего верхнего положения в крайнее нижние положение:

.

Тогда

.

Если подставить диаметр оси маятника D_о, получим основную расчетную:

. (5)

Масса маятника равна сумме масс оси маятника m_о, массы диска m_d и массы кольца m_к:

.