2.2.2 Нечеткая логика и ее особенности

Нечеткая логика может быть рассмотрена как расширение многозначной классической логики. Ее конечной целью является создание базиса для формализации приближенных рассуждений, используя теорию нечетких множеств. Рассмотрим простейший вариант нечеткой логики – нечеткая пропозиционная логика.

Для того чтобы иметь дело с приближенным высказыванием нечеткая логика использует понятие нечеткого высказывания (fuzzy proposition), значение истинности которого описывается с помощью нечетких множеств.

Рассмотрим простое нечеткое высказывание типа “х есть P ”. Предположим, например, что x является лингвистической переменной, обозначающей возраст человека, а свойство P описывается в лингвистической форме как «молодой». Предположим, что универсум представляет собой численную шкалу , представляющую собой возраст людей.

Рассмотрим определение значения истинности для высказывания «х – молодой», полученного заменой на конкретный индивид, например такой: «Сергей – молодой». Значение истинности конкретного высказывания определяется степенью принадлежности возраста Сергея (например,45 лет) к нечеткому множеству «молодой».

На рис. 2.8 показан пример функций принадлежности для определения значений истинности нечетких высказываний.

Рис. 2.8. Пример функций принадлежности нечетких высказываний

Нечеткая логика, как и любая формальная логическая система, состоит из трех основных компонентов: совокупность нечетких высказываний (правильно построенных формул); совокупность нечетких логических операций и совокупность нечетких правил вывода.

2.2.2.1 Типовые нечеткие логические операции

Нечеткие логические операции могут быть введены различными способами. Рассмотрим типовые нечеткие логические операции, используемые в прикладных задачах управления.

Поскольку значения истинности нечетких предикатов описываются нечеткими множествами, то для введения операций нечеткой логики будем использовать операции нечетких множеств.

Определение: нечеткая конъюнкция (Fuzzy conjunction или fuzzy AND).

Значение истинности нечеткой конъюнкции определяется следующим образом:

= ,

где - значения истинности нечетких предикатов ,  соответственно.

Определение: нечеткая дизъюнкция: (Fuzzy disjunction или fuzzy OR). Значение истинности нечеткой конъюнкции определяется следующим образом:

= ,

где - значения истинности нечетких предикатов ,  соответственно.

Определение: нечеткое отрицание (Fuzzy negation). Значение истинности нечеткого отрицания определяется следующим образом:

= ,

где - значение истинности нечеткого предиката .

Нечеткая импликация или нечеткое правило

Нечеткая импликация или нечеткое правило (Fuzzy implication или a fuzzy rule) представляет собой следующее выражение:

ЕСЛИ есть , ТО есть ,

где  и - лингвистические переменные, определенные нечеткими множествами на универсумах  и соответственно. В символьной форме запись имеет следующий вид: .

Часть «ЕСЛИ» (х есть ) называется антецедентом (the antecedent) или посылкой. Часть «ТО» ( есть ) называется следствием (consequence) или заключением.

Определение: Нечеткая импликация (Fuzzy implication). Значение истинности нечеткой импликации определяется следующим образом:

= ,

где есть операция нечеткой конъюнкции (fuzzy AND operation) и - значения истинности нечетких предикатов соответственно.

Интерпретация нечеткой импликации, данная в этом определении, называется импликацией Мамдани (Mamdani implication).

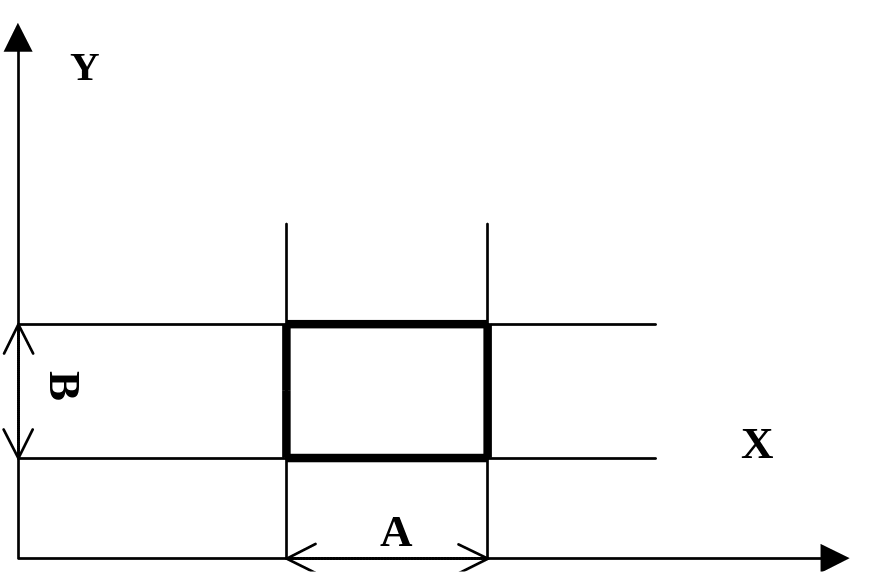
На рис. 2.9 показаны различные интерпретации нечеткой импликации R.

(а)

(б)

Рис. 2.9.(а, б) Две интерпретации нечеткой импликации

Первая интерпретация (рис. 2.9 (а)) представляет импликацию Мамдани: . Вторая интерпретация (рис. 2.9,б) представляет так называемую материальную импликацию, или Булеву импликацию и означает следующее:

Мы будем использовать первую интерпретацию. При этом нечеткое множество R может быть описано как

= A B = ,

где * есть оператор нечеткой конъюнкции ( fuzzy AND operator), т.е.

= .

Примечание. Как принято в литературе по нечетким множествам, знаки интеграла « » и деления «/» в приведенной выше формуле используется только для указания непрерывной совокупности точек .

Примечание. Заметим, что в литературе предложено много определений нечетких логических операций. В общем случае, эти операции называются -нормы и -конормы. Популярной альтернативой введенному выше определению нечеткой импликации являются следующие ниже:

Импликация Лукашевича (Lukasiewicz’s implication):

= ;

Импликация Ларсена (Larsen implication):

= ;

Импликация Заде (Zadeh implication):

= .

Популярной альтернативой введенным выше определениям нечеткой конъюнкции и дизъюнкции являются следующие:

.