1.3. Приклад побудови лінії перетину кривої поверхні з багатогранною.
На рисунку 4 показано приклад побудови лінії перетину кривої поверхні (півсфери) з багатогранною (призмою).
В даному випадку розв’язання задачі зводиться до того, що, по-перше, необхідно знайти точки перетину ребер призми з поверхнею півсфери.
Для цього через ребра призми проводять допоміжні січні площини τ, які будуть одночасно перетинати криву поверхню півсфери по дугам, а призму- по ребрам та прямим (на гранях), які розташовані паралельно П2. Таким чином отримаємо точки 1, 2, 3, 4, 5 та 7, як результат перетину відповідних дуг (дивись на П2) з відповідними ребрами чи прямими призми.
Слід зазначити, що обов’язково необхідно провести січну площину (τ12), яка буде перетинати півсферу по головному меридіану, а грані призми - по прямим, які паралельні ребрам.
Рис. 3. Побудова лінії перетину кривих поверхонь.
Спочатку на П2 отримують фронтальні проекції точок перетину головного меридіану з призмою (52 і З2). Горизонтальні ж проекції їх знаходять по лініям зв'язку. Аналогічним шляхом за допомогою інших січних площин (τ) отримаємо точки 1, 2, 4, 6 та 7. З'єднавши всі знайдені точки з урахуванням видимості отримаємо лінію перетину.
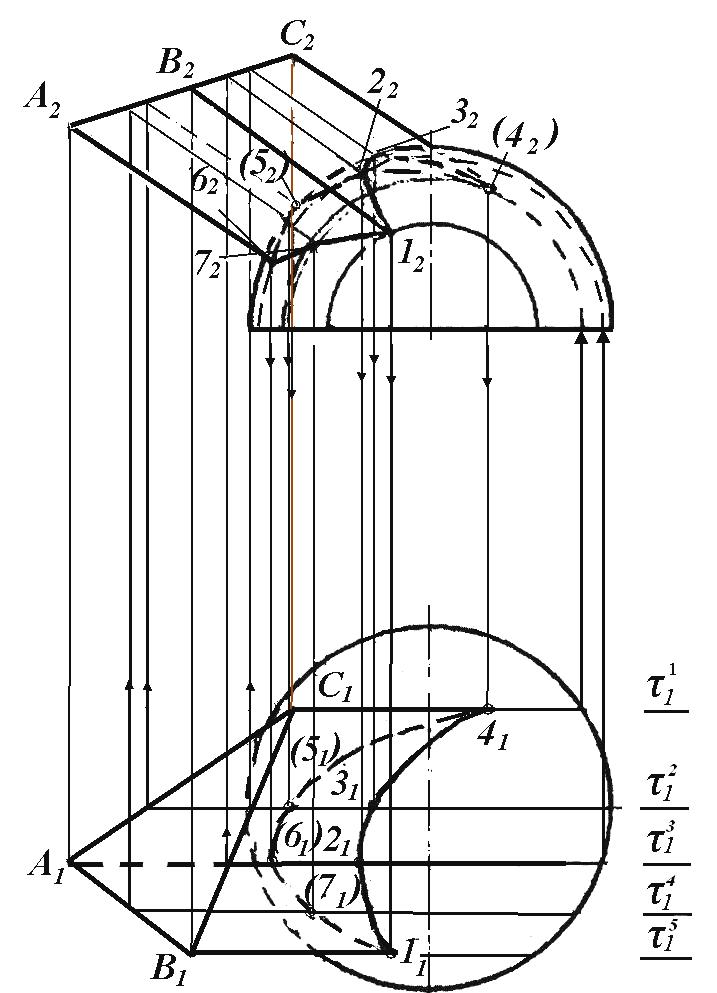
Рис. 4. Побудова лінії перетину кривої поверхні з багатогранною.
2. Розгортки поверхонь. Властивості однозначності. Спосіб нормального перерізу. Спосіб розгортання. Спосіб трикутників.
Розгорткою називається плоска фігура, утворена при суміщенні поверхні геометричного тіла з площиною. Можна сформулювати простіше.
Розгортка - плоска фігура, утворена послідовним суміщенням всіх плоских елементів поверхні в одну площину без розривів та складок.
Розгортка широко застосовується в техніці при виготовленні поверхонь різних деталей. Багато технічних конструкцій виготовляють з листового матеріалу, а заготовки таких конструкцій уявляють собою їх розгортки (повітроводи для промислової вентиляції, труби, бункери, деталі різних будівельних та підйомно-транспортних механізмів...).
Поверхні, які можна повністю сумістити з площиною без розривів чи складок, називають розгортними. До таких відносяться всі гранні поверхні, циліндричні, конічні та торсові поверхні. Характерною ознакою їх є те, що вони мають ребро звороту і дві нескінченно близькі твірні, які перетинаються у власній точці.
Є лише дві криві поверхні, розгортка яких будується дуже просто. Це прямий круговий конус та прямий круговий циліндр. Розгортка поверхні прямого кругового конуса є сектором круга радіуса, який дорівнює твірній конуса, а кут сектора обчислюється по формулі: φ = R•360º/l, де R - радіус основи конуса, а l - довжина твірної конуса. Приклад побудови розгортки поверхні прямого кругового конуса наведено на рисунку 5.
Рис. 5. Побудова розгортки прямого кругового конуса.
Розгортка ж прямого кругового циліндра обертання (див. рис. 6) є прямокутником, висота якого дорівнює висоті циліндра, а ширина -довжині кола основи, тобто 2πR.
Рис. 6. Побудова розгортки прямого кругового циліндра.
Для багатьох поверхонь будують наближені розгортки за допомогою описування чи вписування багатогранних поверхонь. Криві лінії таких поверхонь замінюють на вписані чи описані багатокутники.
Усі інші поверхні, як лінійчасті, так і криволінійчасті просто (елементарними побудовами) розгорнути не можна. Якщо ж є необхідність в розгортці, то її називають умовною.
Поверхню та її розгортку можна розглядати як множину точок, між якими встановлюється взаємно однозначна відповідність. Ця відповідність володіє наступними основними властивостями:
- прямій на поверхні відповідає пряма на розгортці;
- паралельним прямим на поверхні відповідають паралельні прямі на розгортці;
довжини ліній на поверхні та на розгортці рівні;
зберігається рівність кутів між лініями на поверхні та на розгортці;
площа фігури на поверхні дорівнює її площі на розгортці.
Загальним способом побудови розгортки будь-яких поверхонь (кривих) є попередня апроксимація їх гранними поверхнями (в дану криву поверхню вписується або описується гранна поверхня, розгортка якої і будується). Нижче розглянемо різні способи побудови розгорток.
Спосіб нормального перерізу.
Цей спосіб застосовують для побудови розгортки призматичних та циліндричних поверхонь.
Нормальним перерізом називають переріз площиною, яка перпендикулярна до ребер призми (твірних циліндра). На рисунку 7 показано приклад побудови розгортки похилої трикутної призми АВСDEF.
Рис. 7. Побудова розгортки похилої призми способом нормального перерізу.
Бічні ребра призми займають фронтальне положення, на П2 вони будуть в натуральну величину.
Фронтально - проекціююча площина β, яка перпендикулярна до бічних ребер, визначить нормальний переріз 123 призми.
Знаходимо лінію перетину (123) площини β з поверхнею похилої призми: (123) = β ∩Ф.
Фронтальна проекція лінії перетину (122232) буде співпадати з проекцією площини β на П2 - β 2.
Горизонтальна проекція лінії перетину - (112131) знаходиться по лініям зв’язку.
Відповідні точки на ребрах з’єднують ламаною лінією з урахуванням видимості граней призми на П1. Участок 2131 на П1 буде невидимим (лежить на невидимій грані).
Розташувавши цей переріз паралельно до площини проекцій П1, отримаємо його натуральну величину 111211311.
Виконаємо перетворення. Перетворимо 122232 в 121221321 паралельно П1. Розташуємо в вільному місці креслення на П2 паралельно x12 пряму 121221321 , яка рівна прямій 122232 .
Знайдемо по лініям зв’язку горизонтальну проекцію перерізу - 111211311 - натуральну його величину.
Цим способом можна будувати розгортку похилого циліндра, коли до якоїсь площини проекцій його твірні будуть паралельними. Достатньо вписати в циліндр багатогранну (наприклад, дванадцятигранну) призму.
Так як бічні ребра призми паралельні між собою, а сторони нормального перерізу перпендикулярні до них, то на розгортці призми бічні ребра також будуть паралельними між собою, а сторони нормального перерізу розгорнуться в одну пряму. Тому для побудови розгортки призми потрібно відкласти в вільному місці аркушу паперу на будь-якій прямій натуральні величини сторін нормального перерізу: 1020=111211, 20З0=211311, З010=311111, а потім через точки 10, 20, З0 і 10 провести прямі, які перпендикулярні до цієї прямої.
Тепер необхідно відкласти на цих перпендикулярах в обидва кінці (вверх - вниз) від прямої 1010 відрізки бічних ребер, на які їх ділить площина β на площині проекцій П2 (тут натуральна величина бічних ребер). Наприклад, від точки 10 вверх відрізок 10D0, який дорівнює 12D2., а вниз 10А0, який дорівнює 12А2.
Якщо з'єднати відрізками прямих кінці відкладених відрізків, то отримаємо розгортку бічної поверхні призми. Добудувавши до цієї розгортки обидві основи призми, одержимо її повну розгортку.
Цим способом можна будувати розгортку похилого циліндра, коли до якоїсь площини проекцій його твірні будуть паралельними. Достатньо вписати в циліндр багатогранну (наприклад, дванадцятигранну) призму.
Спосіб розгортання.
Такий спосіб застосовують для побудови розгортки призм та циліндрів, коли бічні ребра (твірні) поверхні та хоча б одна з її основ паралельні будь-якій площині проекцій.
На рисунку 8 наведено приклад побудови розгортки похилого еліптичного циліндра.
Рис. 8. Побудова розгортки похилого циліндра способом розгортання.
Спочатку коло основи розбивають на 12 рівних частин (або на 6, 8...), в циліндр вписують похилу призму. Розгортка бічної поверхні циліндра буде складатися з дванадцяти граней призми.
Як видно з рисунка 8, праве контурне ребро вписаної призми (дивись горизонтальну проекцію) приймемо за вісь. Обертаючись навколо неї, вершини основ призми рухатимуться по траєкторіях, перпендикулярних до осі. Кожна грань вписаної призми є паралелограмом, сторони якого відомі: більші сторони (нв) зображені без спотворення на П1, а менші на П2 . Послідовно будують точки 10, 20, 30,...120, 1о (крива , що їх з'єднує - розгортка видимої (на П2 основи)) та точки, з яких складається розгортка другої основи (верхня крива лінія на розгортці).
Ці криві обмежують розгортку бічної поверхні. Якщо ж необхідно побудувати повну розгортку, то до бічної поверхні добавляють дві (як в цьому випадку) основи, які на П2 зображені в натуральну величину.
Спосіб тріангуляції.
Спосіб трикутників (тріангуляції) застосовується для побудови розгортки пірамідальних, торсових та конічних поверхонь (крива поверхня в даному випадку замінюється вписаною багатогранною з трикутними гранями, яка і розгортується).
Розгортка бічної поверхні піраміди складається з трикутників - граней піраміди. Тому побудова розгортки піраміди зводиться до побудови трикутників в натуральну величину.
Для побудови ж розгортки конуса достатньо в нього вписати піраміду. Всі ж інші побудови виконують так, як і в випадку з пірамідою.
На рисунку 9 показана побудова розгортки тригранної піраміди. Визначення натуральних величин бічних ребер піраміди виконано способом обертання їх навколо горизонтально - проекціюючої осі i, яка проходить через вершину S.
Всі ребра повернуті до положення, паралельного площині проекцій П2. При цьому на фронтальній площині проекцій отримаємо натуральну величину ребер: S21A21, S21В21, S21C21.
Для побудови розгортки із довільної точки Sо проведемо пряму, на якій відкладемо натуральну величину ребра SоАо = S21A21.
З точки Sо робимо засічку радіусом, який дорівнює нв ребра SВ (S21В21), а із точки Ао - засічку радіусом, рівним стороні основи піраміди АВ=А1В1.
В результаті отримаємо точку Во і трикутник SоАоВо (це нв грані SАВ). Аналогічно на основі сторони SоАо побудуємо трикутник SоАоСо і на основі сторони SоСо - трикутник S0С0В0.
Основу АВС піраміди ми маємо в натуральну величину на П1. Добудувавши трикутник АоВоСо, рівний трикутнику А1В1С1 до розгортки бічної поверхні, отримаємо повну розгортку піраміди.
Рис. 9. Побудова розгортки піраміди.
Нижче наведено індивідуальні варіанти завдань «Перетин багатогранних поверхонь та їх розгортки» (таблиця 1) та індивідуальні варіанти завдань «Перетин кривих поверхонь та їх розгортки» (таблиця 2). А на рисунках 10 та 11 - приклади виконання завдань на 2-х аркушах паперу формату А3.
Таблиця 1
Індивідуальні
варіанти завдань «Перетин багатогранних
поверхонь та їх розгортки».
Продовження таблиці 1
Продовження таблиці 1
Таблиця 2
Індивідуальні варіанти завдань «Перетин кривих поверхонь та їх розгортки».
Продовження Таблиці 2
Продовження Таблиці 2
