МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

ДВНЗ ПРИДНШРОВСЬКА ДЕРЖАВНА АКАДЕМІЯ БУДІВНИЦТВА ТА

АРХІТЕКТУРИ

Кафедра нарисної геометрії та графіки

Методичні вказівки «Перетин поверхонь та їx розгортки»

до практичних занять та самостійної роботи студентів

напряму підготовки 6.060101 – «Будівництво»

денної та заочної форм навчання

Дніпропетровськ 2014

Методичні вказівки «Перетин поверхонь та їx розгортки» до практичних занять та самостійної роботи студентів напряму підготовки 6.060101 – «Будівництво» денної та заочної форм навчання / К. К. Мірошниченко -Дніпропетровськ: ДВНЗ ПДАБА, 2014.

Методичні вказівки призначені для засвоєння теоретичного матеріалу та виконання графічної роботи "Перетин поверхонь та їх розгортки" студентами технічних спеціальностей. Вони містять теоретичний матеріал з прикладами розв’язання задач по даній темі, варіанти індивідуальних завдань до графічної роботи та приклади їх виконання.

_{Укладач: Мірошниченко К. К., д. т. н., професор кафедри нарисної геометрії та графіки ДВНЗ ПДАБА.}

_{Відповідальний за випуск: Ткач Д. І., к. т. н., проф., зав. кафедри нарисної геометрії та графіки ДВНЗ ПДАБА.}

_{Рецензент: Краснюк А. В., к. т. н., доц., зав. кафедри інженерної графіки ДВНЗ «Дніпропетровський національний університет залізничного транспорту ім. ак. В. Лазаря на»}

_{Затверджено на засіданні кафедри нарисної геометрії та графіки ДВНЗ ПДАБА.}

_{Протокол № 8 від}

_{« 26 » 03 2014 р.}

_{Зав. кафедри нарисної геометрії та графіки Ткач Д. І.}

_{Затверджено на засіданні Президії методичної ради ДВНЗ ПДАБА}

_{Протокол № 8 (97) від}

_{« 13 » 05 2014 р.}

ЗАГАЛЬНІ ПОЛОЖЕННЯ.

Дані методичні вказівки призначені для засвоєння теоретичного матеріалу та виконання графічної роботи "Перетин поверхонь та їх розгортки" студентами технічних спеціальностей. Вони містять теоретичний матеріал з прикладами розв’язання задач по даній темі, варіанти індивідуальних завдань до графічної роботи та приклади їх виконання.

1. Взаємний перетин поверхонь.

Основні відомості по темі.

Поверхні будівельних деталей, інженерних конструкцій, будівель, деталей машин та механізмів уявляють собою поєднання різних геометричних поверхонь - призм, циліндрів, конусів та інших поверхонь, які перетинаються між собою. Лінію, спільну для двох поверхонь, які перетинаються, називають лінією перетину (лінією переходу).

Для її знаходження визначають проекції точок, спільних для поверхонь, що розглядаються. Сполучаючи декілька таких точок, отримують шукану лінію взаємного перетину.

При взаємному перетині багатогранників можливі два випадки:

1. один з багатогранників перебуває у проекціюючому положенні, при цьому одна проекція лінії перетину вже є, а другу - необхідно знайти;

2. треба визначити обидві проекції. У цьому випадку можна застосувати спосіб допоміжних січних площин, або допоміжне проекціювання. Ламана лінія перетину двох багатогранних поверхонь може складатися з однієї замкненої вітки ("урізування") чи з двох замкнених віток ("проникнення").

Лінію перетину багатогранників можна знаходити різними способами:

1. по точкам перетину ребер першої поверхні з другою і точкам перетину ребер другої поверхні з першою;

2. по лініям перетину граней першої поверхні з другою поверхнею і лініям перетину граней другої поверхні з першою.

При перетині двох кривих поверхонь (рис. 1) можливі чотири випадки взаємного перетину:

1. наскрізне проникнення, коли лінія перетину розпадається на дві – лінію входу та виходу (див. рис. 1,а);

2. урізання, коли є тільки одна лінія взаємного перетину (див. рис. 1,б);

3. однобічне внутрішнє стикання, коли крива сама себе перетинає в точці дотику (див. рис. 1,в);

4. подвійне стикання, або розпад кривої четвертого алгебраїчного порядку на дві плоскі криві (див. рис. 1 г).

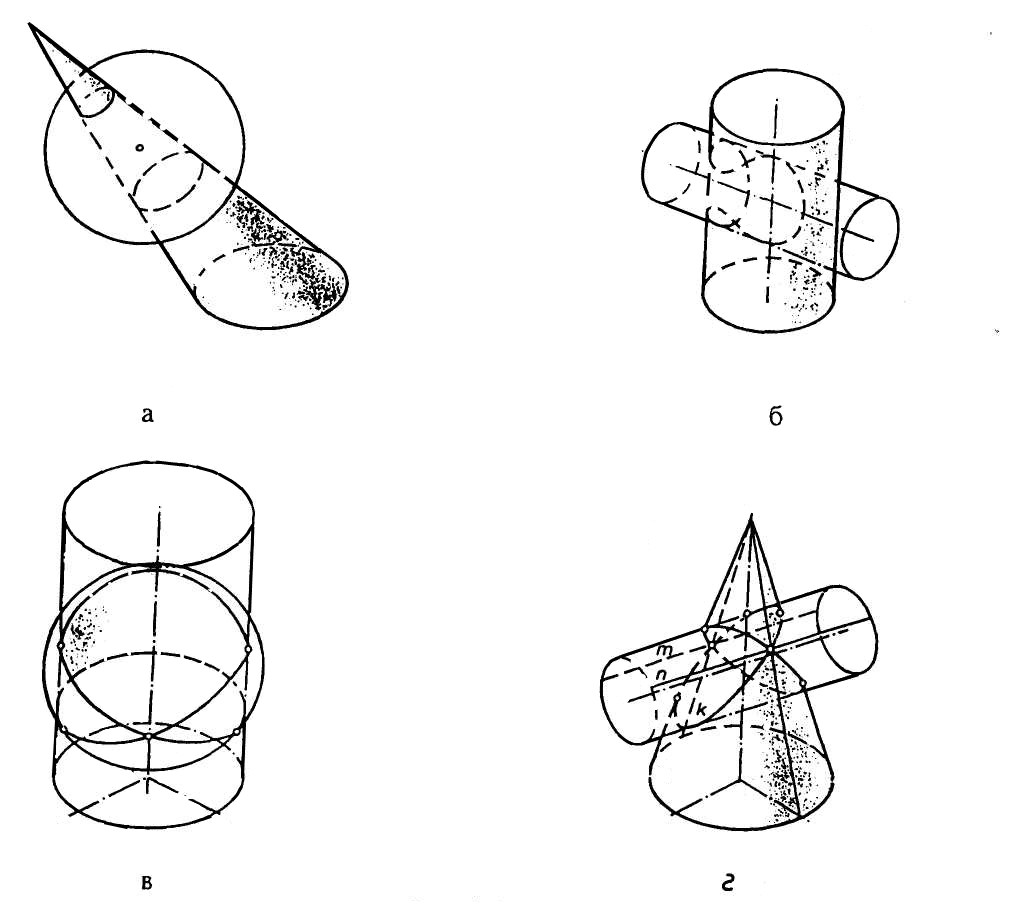
Рис. 1. Перетин кривих поверхонь.