1. Мәліметтерді ендіру және шығару, тағайындау операторы

Тапсырмалардың барлығында ену және шығу мәліметтері нақты типті деп қарастырылсын.

1. Шаршы қабырғасы а берілген. Оның периметрін [P=4a] табу керек.

2. Шаршы қабырғасы а берілген. Оның ауданын [S=a²] табу керек.

3. Тік төртбұрыш қабырғалары a және b берілген. Оның ауданын [S=ab] және периметрін [P=2 (a+b)] табу керек.

4. Шеңбер диаметрі d берілген. Оның ұзындығын табу керек: L=d. Мұндағы  шамасының мәнін 3.14 деп алыңыз.

5. Куб қырының ұзындығы a берілген. Кубтың көлемі [V=a³] мен бетінің ауданын [S=6a²] табу керек.

6. Тік параллелепипедтің қырларының ұзындықтары a, b, c берілген. Параллелепипедтің көлемі [V=abc] мен бетінің ауданын [S=2(ab+bc+ac)] табу керек.

7. R радиусы берілген шеңбердің ұзындығын [L=2R] және осы шеңбермен шектелген дөңгелектің ауданын [S=R²] табу керек. Мұндағы  шамасының мәні 3.14-ке тең деп алынсын.

8. a және b сандары берілген. Олардың арифметикалық орта мәнін табу керек: (a+b)/2.

9. Теріс емес a және b сандары берілген. Олардың геометриялық орта мәнін, яғни олардың көбейтіндісінің квадрат түбірін табу керек: .

10. Нөлдік емес екі сан берілген. Олардың квадраттарының қосындысын, айырмасын, көбейтіндісін және бөліндісін табу керек.

11. Нөлдік емес екі сан берілген. Олардың модульдерінің қосындысын, айырмасын, көбейтіндісін және бөліндісін табу керек.

12. Тік бұрышты үшбұрыштың катеттері a және b берілген. Оның гипотенузасы [ 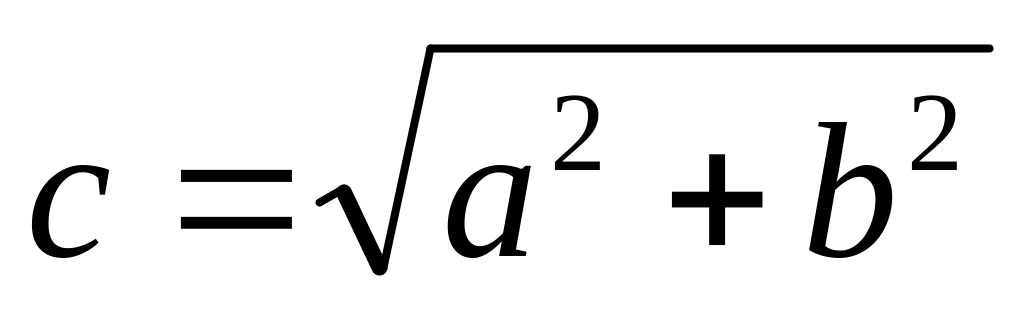] мен периметрін [P=a+b+c] табу керек.

13. Центрлері ортақ және радиустары R₁ мен R₂ (R₁ >R₂) болатын дөңгелектер берілген. Осы дөңгелектердің аудандарын [ , ] және олардың қиылысуынан пайда болған сақинаның ауданын [S₃=S₁-S₂] табу керек. Мұндағы  шамасының мәні 3.14-ке тең деп алынсын.

14. Шеңбер ұзындығы L берілген. L=2R және S=R² теңдіктерін пайдаланып, шеңбер радиусын және осы шеңбермен шектелетін дөңгелек ауданын табу керек. Мұндағы  шамасының мәні 3.14-ке тең деп алынсын.

15. Дөңгелек ауданы S берілген. L=2R және S=R² теңдіктерін пайдаланып, дөңгелек диаметрін және осы дөңгелекті шектейтін шеңбер ұзындығын табу керек. Мұндағы  шамасының мәні 3.14-ке тең деп алынсын.

16. Сан осінде x₁ және x₂ координаттарымен берілген екі нүктенің ара қышықтығын анықтау керек: |x₂ - x₁|.

17. Сан осінде A, B, C нүктелері берілген. AC және BC кесінділерінің ұзындықтарын және олардың қосындысын табу керек.

18. Сан осінде A, B, C нүктелері берілген. C нүктесі А және B нүктелерінің арасында орналасқан. АС және ВС кесінділерінің көбейтіндісін табу керек.

19. Тік төртбұрыштың қарама-қарсы төбелерінің координаттары берілген: (x₁, y₁), (x₂, y₂). Тік төртбұрыштың қабырғалары координат осьтеріне параллель. Берілген тік төртбұрыштың периметрі мен ауданын табу керек.

20. Жазықтықта координаттарымен берілген (x₁, y₁), (x₂, y₂) нүктелерінің ара қашықтығын табу керек. Ара қашықтықты табу формуласы: .

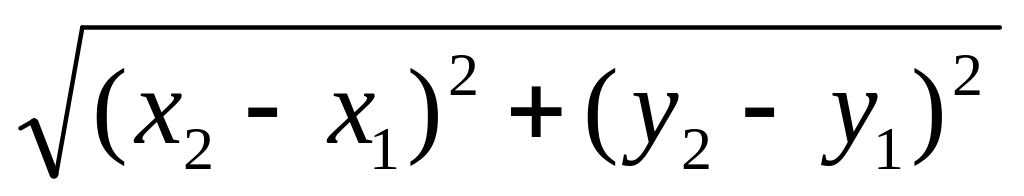21. Жазықтықтағы үшбұрыш төбелері координаттарымен берілген (x₁, y₁), (x₂, y₂), (x₃, y₃). Жазықтықтағы екі нүктенің ара қашықтығын табу формуласын пайдаланып (20-есепті қараңыз) үшбұрыштың периметрі мен ауданын табу керек. Қабырғалары a, b, c үшбұрыштың ауданын есептеуге Герон формуласын пайдаланыңыз: , мұндағы p=(a+b+c)/2 – жарты периметр.

22. a және b айнымалыларының мәндерін ауыстырып, a мен b-ның жаңа мәндерін шығару керек.

23. a,b,с айнымалылары берілген. Олардың мәндерін келесі тәртіппен ауыстырып, алынған жаңа мәндерді шығару керек: а-ны b-ға, b-ны c-ға, c-ны a-ға.

24. a,b,с айнымалылары берілген. Олардың мәндерін келесі тәртіппен ауыстырып, алынған жаңа мәндерді шығару керек: а-ны c-ға, c-ны b-ға, b-ны a-ға.

25. Мәні берілген х үшін y=3x⁶ – 6x² – 7 функциясының мәнін есептеу керек.

26. Мәні берілген х үшін y=4(x – 3)⁶ – 7(x – 3)³ + 2 функциясының мәнін есептеу керек.

27. а саны берілген. Қосымша айнымалыны және үш рет көбейту амалын пайдаланып а⁸ мәнін есептеу керек. Ол үшін рет-ретімен а², а⁴ және а⁸ мәндерін есептеңіз де, а-ның барлық дәрежелерін шығарыңыз.

28. а саны берілген. Қосымша айнымалыны және бес рет көбейту амалын пайдаланып а¹⁵ мәнін есептеу керек. Ол үшін рет-ретімен а², а³, а⁵, а¹⁰ және а¹⁵ мәндерін есептеңіз де, а-ның барлық дәрежелерін шығарыңыз.

29. бұрышының мәні градуспен берілген (0< <360). 180= радиан екенін ескеріп, берілген бұрыштың мәнін радиан арқылы есептеу керек. Мұндағы  шамасының мәнін 3.14 деп алыңыз.

30. бұрышының мәні радианмен берілген (0< <2). 180= радиан екенін ескеріп, берілген бұрыштың мәнін градус арқылы есептеу керек. Мұндағы  шамасының мәнін 3.14 деп алыңыз.

31. Т температурасы Фаренгейт градусымен берілген. Осы температура мәнін Цельсий градусымен анықтау керек. Цельсий бойынша Т_С температурасы Фаренгейт бойынша T_F температурасымен келесі қатынас бойынша байланысқан: Т_С=( T_F - 32)5/9.

32. Т температурасы Цельсий градусымен берілген. Осы температура мәнін Фаренгейт градусымен анықтау керек. Цельсий бойынша Т_С температурасы Фаренгейт бойынша T_F температурасымен келесі қатынас бойынша байланысқан: Т_С=( T_F - 32)5/9.

33. x кг конфеттің бағасы а тг екені белгілі. Салмағы 1 кг және у кг осындай конфеттің құны қанша екенін анықтау керек.

34. x кг шоколадты конфеттің бағасы а тг және y кг иристің бағасы b тг екені белгілі. Салмағы 1 кг шоколадты конфет пен 1 кг иристің құны қанша екенін және шоколадты конфеттің бағасы иристің бағасынан неше есе артық екенін анықтау керек.

35. Қозғалыссыз судағы қайық жылдамдығы V км/сағ, өзен ағысының жылдамдығы U км/сағ (U<V). Қайықтың көлдегі қозғалыс уақыты Т₁ сағ, ал өзен бойымен (ағысқа қарсы) – T₂ сағ. Қайықтың жүрген жолы S-ті анықтау керек (жол = уақыт  жылдамдық). Ағысқа қарсы қозғалған кезде қайықтың жылдамдығы ағыс жылдамдығына тең шамаға кемитінін ескеру керек.

36. Бірінші автокөліктің жылдамдығы V₁ км/сағ, екіншісінікі – V₂ км/сағ және олардың ара қашықтығы S км. Егер автокөліктер біріне-бірі жақындау бағытында қозғалса, онда олардың ара қашықтығы Т сағаттан соң неге тең? Бұл қашықтық бастапқы қашықтық пен автокөліктер жүрген жалпы жолдың айырымының модуліне тең; (жалпы жол = уақыт  қосынды жылдамдық).

37. Бірінші автокөліктің жылдамдығы V₁ км/сағ, екіншісінікі – V₂ км/сағ және олардың ара қашықтығы S км. Егер автокөліктер бір-бірінен алыстау бағытында қозғалса, онда олардың ара қашықтығы Т сағаттан соң неге тең? Бұл қашықтық бастапқы қашықтық пен автокөліктер жүрген жалпы жолдың айырымының модуліне тең; (жалпы жол = уақыт  қосынды жылдамдық).

38. ax+b=0 сызықтық теңдеуінің a және b коэффициенттері берілген. Оның шешімін табу керек (а – 0-ден өзге сан).

39. ax²+bx +c=0 квадрат теңдеуінің коэффициенттері a, b және с берілген (а – 0-ден өзге сан) және теңдеу дискримананты оң сан екені белгілі болса, онда теңдау түбірлерін табу керек. Анықталған түбірлердің алдымен кішісін, сонан соң үлкенін шығару керек. Квадрат теңдеу түбірлері келесі өрнек арқылы анықталады: 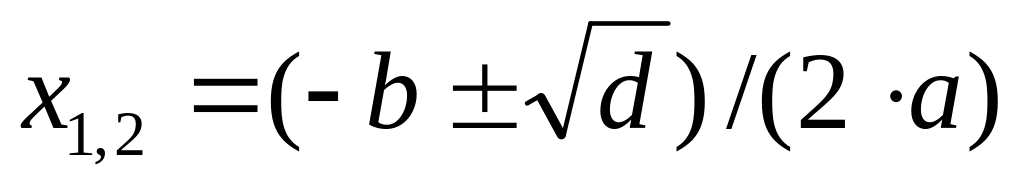, мұндағы d=b²-4ac.

40. Коэффициенттері a₁,b₁,c₁,a₂,b₂,c₂ арқылы берілген және алдын-ала жалғыз шешімі бар екені белгілі. Келесі сызықтық теңдеулер жүйесін шешу керек:

a₁ x+b₁ y=c_1,

a₂ x+b₂ y=c₂.

Ол үшін келесі формулаларды пайдаланыңыз:

x=(c₁b₂-c₂b₁)/d, y=(a₁c₂-a₂c₁)/d, d=a₁b₂-a₂b₁.