Задания для самостоятельной работы

1. Доказать ограниченность последовательностей:

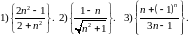
2. Доказать неограниченность последовательностей:

3. Бесконечно малые и бесконечно большие последовательности.

Определение. Последовательность называется бесконечно малой, если для любого положительного числа можно указать такой номер N, зависящий от , что при n все элементы этой последовательности удовлетворяют неравенству .

С помощью кванторов (для любого) и (существует) определение записывается так:

бесконечно. малая последовательность .

Пример 1. Доказать, пользуясь определением, что последовательность является бесконечно малой.

Решение. Докажем, что для любого заданного положительного числа (сколь угодно малого) можно указать номер N, начиная с которого все элементы данной последовательности удовлетворяют неравенству .

Сначала решаем это неравенство относительно : . Этому неравенству удовлетворяет бесконечное множество натуральных числе. Например, если , то неравенству будут удовлетворять числа поэтому в качестве номера можно взять любое из них. Если , то можно взять Значит, в качестве номера можно взять, например, наименьшее из тех. натуральных чисел, которые удовлетворяет неравенству , а именно, 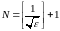. Здесь обозначено – целая часть числа .

Осталось показать, что начиная с найденного номера , все элементы данной последовательности удовлетворяют неравенству . Действительно, если , то , т.е. , а это по определению и означает, что последовательность  бесконечно малая.

Найденный номер зависит от . Чтобы выяснить характер зависимости, составим таблицу

	0,1	0,01	0,001	0,00001
	4	11	34	101

Зависимость от оказалась обратной: чем меньше число , тем больше номер , начиная с которого все элементы последовательности попадают в -окрестность нуля, т.е. в интервал . Более подробная запись последовательности , где , иллюстрирует полученный результат:

Мы видим, что начиная с , все члены последовательности становятся (и остаются) меньше ; начиная с все члены становятся (и остаются) меньше . ▲

Пример 2. Пусть . Покажем, что – бесконечно малая последовательность.

Решение. Если , то, очевидно, . Пусть . Зададим произвольное число >0. Докажем, что для этого можно указать номер N, начиная с которого все элементы последовательности удовлетворяют неравенству .

Сначала решаем это неравенство относительно . Так как , то неравенство можно прологарифмировать: , что равносильно неравенству (ведь по условию . В качестве номера можно взять любое натуральное число , например, .

Действительно, если , то , а это и означает, что последовательность является бесконечно малой.

Например, для последовательности получаем и соответствующая таблица зависимости от выглядит так:

	0,1	0,01	0,001
N	4	7	9

▲

Определение. Последовательность называется бесконечно большой, если для любого положительного числа можно указать такой номер , что при все элементы последовательности удовлетворяют неравенству .

С помощью кванторов и определение записывается так:

 бесконечно большая последовательность

Последнее неравенство можно представить в виде совокупности двух неравенств . Если последовательность бесконечно большая, то для любого положительного (сколь угодно большого) числа А можно указать такой номер N, начиная с которого все элементы последовательности попадают в бесконечные интервалы ( ) или ( ). Таким образом, в интервале (А; А) остается лишь конечное число элементов.

Пример 3. Доказать, пользуясь определением, что последовательность является бесконечно большой.

Решение. Докажем, что для любого заданного положительного числа A (сколь угодно большого) можно найти номер N, начиная с которого . Решая последнее неравенство относительно , получаем . Можно взять, например, . Действительно, если , то , а это по определению означает, что последовательность бесконечно большая. Выясним характер зависимости номера от , используя таблицу.

	10	100	1000	10000
	11	101	1001	10001

Зависимость оказалась прямой: чем больше число , тем больше номер , начиная с которого все элементы последовательности удовлетворяют неравенству . ▲

Сформулируем основные свойства бесконечно малых последовательностей.

Теорема 1. Сумма бесконечно малых последовательностей и есть бесконечно малая последовательность.

Теорема 2. Бесконечно малая последовательность ограничена.

Теорема 3. Произведение бесконечно малой последовательности на ограниченную последовательность – бесконечно малая последовательность.

Теорема 4. Если – бесконечно большая последовательность, то, начиная с некоторого номера, определена последовательность , которая является бесконечно малой. Если все элементы бесконечно малой последовательности не равны нулю, то последовательность – бесконечно большая.

Пример 4. Доказать, что – бесконечно малая последовательность.

Решение. 1) Представим в виде суммы: . . Последовательность является бесконечно малой (пример 1); легко доказать с помощью определения, что последовательность – бесконечно малая. А сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

2) Представим в виде суммы: . Поскольку , то . Значит, справедливы неравенства и . Поэтому и – бесконечно малые последовательности. Осталось применить теорему 1 о сумме бесконечно малых последовательностей.

3) Представим в виде произведения . Последовательность ограничена (пр. 3 п.3), – бесконечно малая последовательность. В силу теоремы 3 – бесконечно малая. ▲

Пример 5. Доказать, что – бесконечно большая последовательность.

Решение. 1) Рассмотрим последовательность . Обозначим . В примере 1 доказано, что – бесконечно малая последовательность. Легко доказать с помощью определения, что последовательность также является бесконечно малой. Можно также рассматривать как произведение двух бесконечно малых последовательностей и , тогда по теоремам 2 и 3 – бесконечно малая последовательность. В силу теоремы 1 – бесконечно малая, а в силу теоремы 4 – бесконечно большая.

Задачи 2) и 3) рассмотреть самостоятельно.