1. Метод математической индукции.

Во многих разделах математики приходится доказывать истинность утверждений на множестве натуральных чисел. Часто это удается сделать методом математической индукции, в основе которого лежит

Теорема. Пусть некоторое множество натуральных чисел 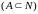удовлетворяет следующим двум условиям: 1) 1 , 2) если , то . Тогда множество содержит все натуральные числа, то есть .

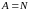Пример 1. Докажем, что для любого натурального числа имеет место равенство

. (1)

Доказательство. Символом обозначается сумма слагаемых вида , индекс суммирования – натуральное число – принимает значения от до :

.

Пусть – множество натуральных чисел, для которых справедливо соотношение (1), т.е. .

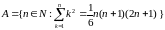1. При условие (1) выполнено: , то есть (проверка базиса)

2. Делаем индукционный шаг. Пусть условие (1) выполняется для некоторого , оно остается справедливым и после прибавления к обеим частям слагаемого :

.

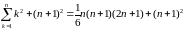Левая часть здесь – это 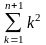. Правая часть преобразуется к виду

Таким образом,

Отсюда следует, что и . Из утверждения теоремы следует, что , то есть наша формула справедлива для любого натурального . ▲

Пример 2. Докажем, что для любого натурального числа имеет место равенство (формула для суммы членов арифметической прогрессии):

. (2)

Доказательство. 1. Сначала проверим базис:

при имеет место равенство .

2. Далее делаем индукционный шаг. Пусть для некоторого натурального числа утверждение , т.е. равенство (2) справедливо; покажем, что отсюда следует и его справедливость для числа , следующего за . Действительно, прибавим к обеим частям верного равенства (2) число ( ) и преобразуем правую часть:

.

Но это и означает справедливость формулы (2) для , т.е. справедливость утверждения 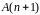. В силу метода математической индукции формула справедлива для любого натурального . ▲

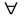
Пример 3. Доказать, что при число кратно 19.

Доказательство. Положим . При это утверждение легко проверяется: , очевидно, делится на 19. Предположим, что , т.е. число кратно 19. Подставим в это число вместо и сведем полученное выражение к сумме двух слагаемых:

.

Так как каждое из слагаемых кратно 19, то . ▲

Пример 4^*.

Доказать формулу (бином Ньютона)

. (3)

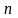Здесь обозначено – число сочетаний из по . Например, . Действительно, из трех элементов 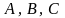можно составить три сочетания по два элемента: . Вычислим еще , тут по определению.

Доказательство формулы (3) проведем методом математической индукции. Пусть

.

1. При формула верна: 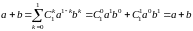. Значит, .

2. Делаем индукционный шаг. Пусть условие (2) выполняется для некоторого , оно остается справедливым и после умножение обеих частей на :

. (4)

Левая часть здесь – это . Покажем, что правую часть соотношения (4) можно преобразовать к виду .

Сначала разобьем правую часть на два слагаемых:

В сумме выделим первое слагаемое и запишем её в виде:

.

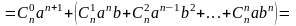
А в сумме выделим последнее слагаемое и запишем её в виде:

.

Теперь справа в (4) получаем:

=

.

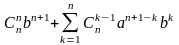Здесь учтено, что .

Преобразуем выражение в скобках:

Теперь правая часть соотношения (4) принимает вид

Окончательно получим

,

А это означает, что и , то есть формула (3) (бином Ньютона) справедлива для любого натурального . ▲

Полезно запомнить формулу (3) и в развернутом виде:

.