6. Характеристические параметры 4х-полюсника.

УРАВНЕНИЯ В ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЯХ

Такие устройства как телефонные и телеграфные линии связи, мно-гокаскадные усилители и многозвенные электрические фильтры могут рассматриваться как 4х-полюсники. Но их работе присущи харак-терные особенности: это большая протяжённость в пространстве и широкий диапазон частот проходящих сигналов. В этих условиях АВСD -коэффициенты, как характеристики для фиксированной частоты, становятся неудобными. В таких случаях уравнения записыва-ют через гиперболические функции и пользуются вторичными /ха-рактеристическими, волновыми/ параметрами 4х-полюсников, к которым относятся:

- характеристические сопротивления Z_C1 и Z_C2 ;

- постоянная передачи g = a +j b четырёхполюсника.

* Характеристические сопротивления Z_C1 и Z_C2 несимметричного 4х-полюсника - это пара сопротивлений, удовлетворяющая следую-щим условиям: входное сопротивление Z₁вх = Z_C1, если 4х-полюс-ник нагружен на Z_C2, и наоборот: сопротивление Z₂вх = Z_C2, если по входу 4х-полюсник нагружен на Z_C1.

З нание этих величин необходимо для согласования 4х-полюсника как по выходу, т.е. с нагрузкой, так и по входу, т.е. с источником си-гнала или блоком питания. В этом случае от источника сигнала /дат-чика/ в нагрузку будет передана максимально возможная мощность.

Сопротивления Z_C1 и Z_C2 находят совместным решением формул [6аб] для входных сопротивлений Z_1ВХ и Z_2ВХ четырёхполюсника.

Для симметричного 4х-полюсника:

[7]

Для несимметричного 4х-полюсника:

[7а]

* Постоянная передачи g= a+j b - это комплексная величина, харак-теризующая передачу сигнала по мощности. По определению пос-тоянная передачи g - это отношение мощностей входного и выходного сигналов, взятое в логарифмическом масштабе:

g = a +j b = , [б/р] . [8]

Здесь а - коэффициент затухания (ослабления) сигнала по мощности,

b - коэффициент изменения фазы “мощностного” сигнала.

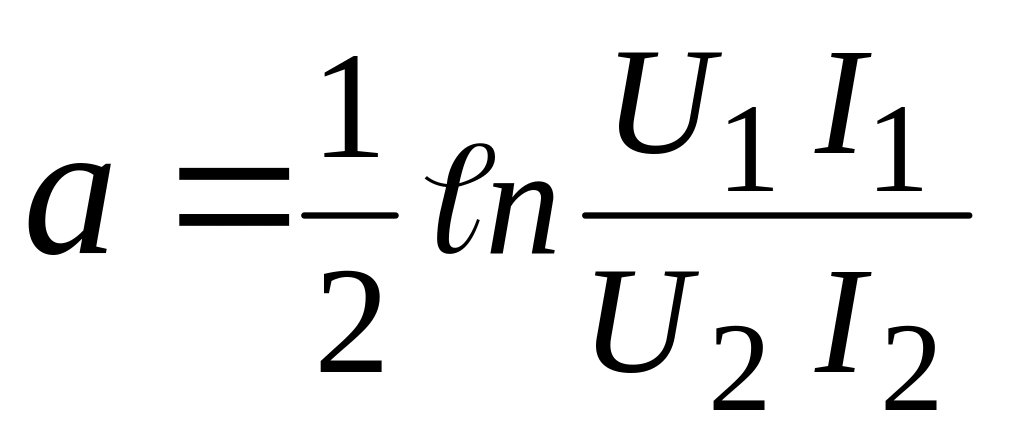Нп, дБ. b = , рад.

Единицы затухания приняты:

на основе натурального логарифма - неперы - Нп,

на основе десятичного логарифма - бел, децибел, ДБ.

Если сигнал, проходя через 4х-полюсник, по мощности уменьшается в 10 раз, то коэффициент затухания будет равен:

а = а =

Соотношение между этими единицами затухания:

1 Б = 1,15 Нп 1 Нп = 0,8686 Б

1 дБ = 0,115 Нп 1 Нп = 8,686 дБ.

Теперь о коэффициенте фазы b четырёхполюсника. Это не сдвиг по фазе между напряжениями или между токами 4х-полюсника, это разность фаз комплексов мощностей на входе и выходе S₁ и S₂.

В случае согласованной нагрузки, когда Zнг = Z_C = Zвх, коэффициент фазы b, действительно, будет равен сдвигу по фазе как между токами, так и между напряжениями: b = ψu1 - ψu2 = ψi1 - ψi2.

КАК РАССЧИТЫВАЕТСЯ ПОСТОЯННАЯ ПЕРЕДАЧИ 4-ПОЛЮСНИКА

* Характеристические параметры 4-полюсника, как и первичные, полностью определяются схемой и параметрами элементов, и могут быть рассчитаны: - по определению (см. выше);

- через сопротивления Zхх и Zкз;

- через первичные АВСD - коэффициенты.

Для симметричного 4х-полюсника:

g = a +j b = , [8а]

По данным опытов холостого хода и короткого замыкания:

; ; ; [8б]

приравнивая в последнем выражении М = е^2а и jφ = j2b, записываем полное выражение постоянной передачи g = a +j b.

Для несимметричного 4х-полюсника расчёт постоянной передачи g через сопротивления Zхх и Zкз довольно громоздок, поэтому приведём лишь следующие расчётные выражения:

g = , т.е. е ^g = ; [9a]

* РЕМАРКА. Атабеков Г.И., ТОЭ, с.251: расчёт постоянной g предпочтительнее вести по [8] или через АВСД - коэффициенты по формулам [8а-9а], так как th g в формуле [8b] не улавливает разницы от перекрещивания входных зажимов 4-полюс-.

Уравнения 4х-полюсника в гиперболических функциях

Переход к уравнениям, записываемым через гиперболические функ-ции ch g и sh g, осуществляется на основе формул [7] и [9а] по соотношениям Эйлера:

; ;

Поскольку фильтры и линии связи являются симметричными четырёхполюсниками, окончательно искомые уравнения имеют вид:

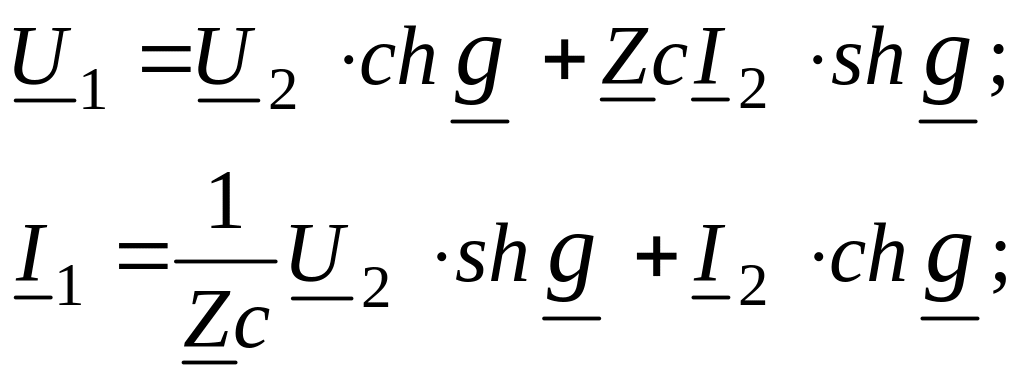[10]

Уравнения для несимметричного 4х-полюсника из-за различия Z_C1 и Z_C2 более громоздки, да и пользуются ими реже. /Атабеков Г.И., с.250/:

;

В заключение напомним, что соотношение А D - В C = 1 здесь равнозначно соотношению ch²g - sh²g = 1.

При исследованиях длинные линии, гирлянды изоляторов на высоковольтных линиях и т.п. представляют каскадным включением не-скольких одинаковых симметричных 4х-полюсников, которое называют цепными схемами. Эти устройства работают при согласованной нагрузке. АВСD -коэффициенты и вторичные параметры Z_C и g здесь очень просто выражаются через параметры одного 4х-полюсника:

Z_{C ц.схемы} = Z_{C звена}, g_схемы = п∙а + jn∙b.

Подробнее о цепных схемах можно прочесть в учебнике Зевеке Г.В, ТОЭ, 1989г., стр.150-152.