2. Переходные процессы в цепях с одним
НАКОПИТЕЛЕМ ЭНЕРГИИ
Общие закономерности и характерные особенности переходных процес-сов в цепях с одним накопителем энергии можно рассмотреть на одном-двух типовых случаях.
Постоянная времени цепи, характер и длительность процесса
при
включении
RL-цепи
на постоянное напряжение
U0.
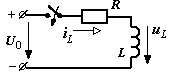
Дано: напряжение U0, параметры R, L .
Требуется: найти законы изменения в переходном процессе тока iL(t), напряжения uL(t), построить их графики.
* В переходном процессе цепь описывается одним уравнением по II закону Кирхгофа. Это дифференциальное уравнение первого порядка.
.
1. Независимые начальные условия переходного процесса: до коммутации цепь была обесточена, поэтому iL(0-) = 0.
2. Принуждённые составляющие: в установившемся режиме индуктивность не оказывает сопротивления постоянному току. Поэтому:
,
.
3. Характеристическое уравнение цепи и его корень:
,
,
τ
=
, с.
Свободные составляющие тока и напряжения будем находить в виде:
Поведение цепи в свободном режиме можно характеризовать как корнем р характеристического уравнения, так и его обратной величиной, имеющей размерность времени. Её называют постоянной времени цепи τ.
Постоянная времени τ - это время, в течение которого свобод-ная составляющая тока или напряжения изменяется в е-раз.
Постоянная времени цепи характеризует инерционность поведения цепи в свободном режиме при любых воздействиях и определяется исключи-тельно соотношением параметров цепи, не зависит ни от величины тока, ни от величины рабочего напряжения, ни от начальных условий процесса. Через постоянную времени определяется практическая длительность пере-ходного процесса.
Рассчитать постоянную времени цепи можно одним следующих способов:
1.
2.
3.
по осциллограмме:
.
Реальные электротехнические устройства - обмотки реле, трансформаторов, двигателей имеют τ = 0,01 - 0,1 с.
4. Для отыскания А и В - постоянных интегрирования необходимо знать начальные (в момент t = 0+) значения тока и напряжения. Ток в индуктивности подчиняется первому закону коммутации: iL (0+) = iL(0-) = 0.
Напряжение на индуктивности uL(0+) находим из уравнения по II закону Кирхгофа: uL(0+) + R∙iL(0+) = U0. uL (0+) = U0.
Тогда постоянные интегрирования: А = i (0+) - iпр (0+) = - I0,
В = uL (0+) - uпр (0+) = +U0.
* Отметим характерную особенность: незаряженная индуктивность в момент включения ведёт себя как разомкнутый элемент: к ней приложено всё напряжение, а ток в ней равен нулю!
5. Итак, полные выражения тока и напряжения в переходном процессе:
u
L
(t)
=
uсв
=
U0∙е
р
t
= U0
∙
В,
iL
(t)
=
i
пр
+
iсв
=
I0
- I0
∙
А.
*
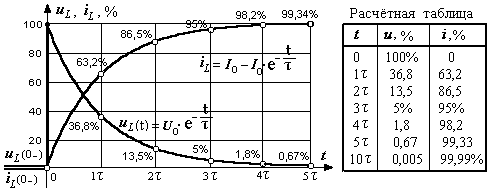Построение
графиков. Пусть I0
= 100%,
U0
= 100%,
t
=
0,
1τ,
2τ,
3τ,
4τ,
5τ.
Из приведенных расчётов и графиков видим, что в цепи с одним накопителем энергии функция монотонно приближается к своему новому установившемуся значению. Такой процесс называют апериодическим.
Теоретически процесс длится бесконечно долго. Поэтому обычно пользуются понятием практической длительности процесса: t пп ≈ 3 ÷ 5 τ.
Постоянная времени цепи, характер и длительность процесса
при включении RС-цепи на постоянное напряжение U0.
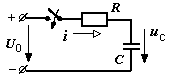
Дано: напряжение U0, параметры R, C .
Требуется: найти законы изменения тока за-ряда ic (t) и напряжения на конденсаторе uc(t),
построить их графики.
Решение изложим совсем кратко.
1. Независимые начальные условия: uc(0-) = 0. τ = RC , с
2. Принуждённые составляющие: iпр(t) = 0, uc пр(t) = U0.
3. Характеристическое уравнение, корень, вид свободных составляющих:
,
;
τ
= RC
, с
iсв(t)
= Ae
pt,
uсв(t)
= Be
pt.
4. Значения тока заряда и напряжения на конденсаторе в момент t = 0:
по закону коммутации uc(0+) = uc(0-) = 0; по закону Ома i(0+) = U0/R = I 0;
Постоянные интегрирования: А =i (0+)-iпр (0+) = I0; В = uc(0+) -uc пр(0+) = U0.
5. Окончательные выражения тока и напряжения в процессе заряда:
iС
(t)
= iсв
=
I0
∙
А;
u
С (t)
= uпр
+ uсв
=
U0-U0∙е
р
t
= U0
∙
В.
* Незаряженная ёмкость в момент включения ведёт себя как короткозамкнутый элемент: напряжение на ней равно нулю, а ток определяется резистором. Постоянная времени τ = RC, длительность процесса tпп = 3 ÷ 5 τ.
* RC-цепь в переходном процессе ведёт себя дуально RL-цепи: ток заря-да конденсатора изменяется так же, как напряжение на индуктивности, а на-пряжение uc как ток при заряде rL - цепи.
Особенности переходных процессов при включении
RL и RC-цепей на синусоидальное напряжение
Включение RL и RС-цепей было рассмотрено при нулевых начальных условиях. Обратим внимание на то, что постоянные интегрирования в выражениях тока и напряжения были равным принуждённым составляющим, взятым с обратным знаком: А = - iL пр (0+) , В = - uc пр (0+).
Из этого следует, что при включении таких же цепей на синусоидальное напряжение возможны два характерных предельных случая:
- если коммутация цепи происходит в момент, когда принуждённая составляющая iL пр (t) = Im·sin (ωt + ψi) проходит через нуль, то переходного процесса по сути не возникает. Математически это условие имеет вид:
ψi = ψu - φ = 0 или ψu = φ.
- если же коммутация произойдёт в момент, когда принуждённая состав-ляющая проходит через амплитудное значение ± Im пр, то ток в переходном процессе, при достаточно большой постоянной времени цепи τ, может достигнуть значения ≈ 2Im пр. Но не более. Математически это возможно при условии: ψu = φ ± π/2.
Ещё раз напомним, что изложенные особенности касаются лишь случаев включения цепей при нулевых начальных условиях.
Примеры расчёта ПП в цепях с одним накопителем энергии