Основы теории пограничного слоя

12.1. Понятие о пограничном слое

Теория движения идеальной жидкости хорошо разработана и обычно дает вполне удовлетворительные результаты при ис­следовании действительных течений (особенно при больших чис­лах Рейнольдса), за исключением областей, расположенных в непосредственной близости от поверхности обтекаемого тела и областей отрыва потока в случае неудобообтекаемых тел. В этих областях на характер течения существенное влияние оказывают силы внутреннего трения жидкости, обусловленные наличием вязкости. Расстояние, на котором происходит изменение скорости от нуля (на поверхности тела) до величины, имеющей место в идеальной жидкости, характеризует область влияния вязкости. При внешнем обтекании по мере удаления от передней критичес­кой точки тела к задней кромке толщина этой области растет.

В рассматриваемом случае весь поток условно можно раз­бить на две области: пристенную область, весьма малой толщи­ны, называемую пограничным слоем, где влияние сил вязкости столь же существенно, как и влияние всех других сил (например, сил давления, сил трения), и область внешнего потока, где влия­ние сил вязкости пренебрежимо мало. Таким образом, погранич­ный слой можно определить как прилегающий к поверхности твердого тела слои жидкости, в котором сосредоточено основное воздействие сил вязкости на тело.

От структуры течения в пограничном слое в значительной мере зависит сопротивление обтекаемого тела, его подъемная сила, аэродинамический нагрев (при сверхзвуковых скоростях) и т. д.

Торможение частиц газа в пограничном слое происходит под воздействием сил, передающих это торможение на некоторое расстояние от тела в глубь потока. Касательные напряжения (силы трения), обусловленные силами вязкости, уменьшают скорости частиц газа в пограничном слое и вызывают их вра­щение, образуя вихри. Изучение структуры и характера течения жидкости или газа в пограничном слое позволяет объяснить такие важные аэродинамические явления, как возникновение срыва потока на обтекаемых телах, образование вихревого сле­да за телом, а также определить силы трения газа на поверхно­сти тела. Теоретически анализ движения газа в пограничном слое сводится к решению системы сложных дифференциальных уравнений. Решение должно удовлетворять граничным услови­ям: на бесконечности скорость потока должна совпадать по ве­личине и направлению со скоростью внешнего потока V₀(x), на поверхности обтекаемого тела скорость должна быть равна нулю.

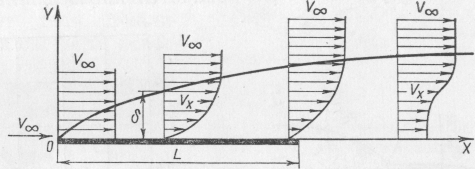
Рис. 12.1.Схематическое изображение

пограничного слоя на плоской пластине

Проблемой сопротивления трения в жидкостях и газах зани­мались многие ученые еще до появления теории пограничного слоя. Среди них Галилей, Кулон, Ньютон, Стоке, Рэнкин, Менде­леев и др. Понятие о пограничном слое впервые было введено Жуковским.

Теоретические разработки теории пограничного слоя были начаты Прандтлем в 1904 г. и развиты Блазиусом, Карманом, Польгаузеном, Милликеном, Г. Шлихтингом и др. Развитию те­ории пограничного слоя посвящено большое количество работ советских ученых Л.С. Лейбензона, Η.Ε. Кочина, А.А. Дород­ницына, В.В. Голубева, Л.Г. Лойцянского, А.П. Мельникова, К.К. Федявского и др. Советские аэродинамики провели ряд важных теоретических и экспериментальных исследований по­граничного слоя, разработали рациональные формы крыльев и фюзеляжей, имеющих малое сопротивление трения и обтекаемых без срыва потока до больших углов атаки.

Рассмотрим вначале течение вязкой жидкости около плоской пластины (рис.12.1). Опыты показывают, что частицы жидкос­ти, соприкасающиеся с поверхностью пластины, полностью за­тормаживаются. По мере удаления от пластины скорость тече­ния увеличивается, асимптотически приближаясь к теоретиче­ской скорости, соответствующей обтеканию невязкой жидко­стью, а в рассматриваемом случае – к скорости внешнего пото­ка V₀ = V_. Это обстоятельство делает неопределенным положе­ние верхней границы пограничного слоя, а следовательно затрудняет определение его толщины. Однако, учитывая, что су­щественное нарастание скорости в пограничном слое происходит у самой стенки и уже на очень малом расстоянии от нее ско­рость незначительно отличается от скорости невозмущенного потока, за толщину пограничного слоя δ можно принять рассто­яние от поверхности обтекаемого тела, на котором скорость по­тока Vx достигает 99,5% скорости внешнего потока. Весьма час­то принимаются и другие определения условной толщины погра­ничного слоя, хотя следует иметь в виду, что зона влияния вяз­кости распространяется от поверхности тела асимптотически и, если принять вместо 99,5% хотя бы 99%, то абсолютная вели­чина толщины пограничного слоя значительно уменьшится. В соответствии с принятым определением толщины δ внеш­няя граница пограничного слоя не является линией тока и с

Рис. 12.2. Структура пограничного слоя при переходе ламинарного течения в турбулентное:

1 – ламинарный слой;

2 – точка перехода;

3 – турбулентный слой;

4 – вязкий подслой;

5 – пластина

лу­жит лишь условным пределом зоны влияния вязкости.

Е

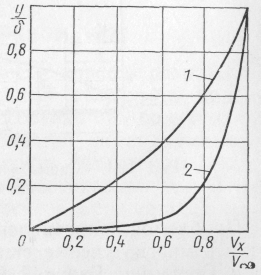
Рис. 12.3.Сравнение эпюр скорости в ламинарном и турбулентном пограничных слоях:

1 – ламинарный слой;

2 – турбу­лентный слой.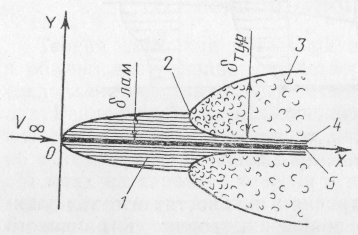

сли обтекаемая пластина достаточно длинна, то структура течения в пограничном слое на разных расстояниях от передней кромки пластины различна. Вблизи передней кромки течение в пределах пограничного слоя слоистое. Такой пограничный слой называется ламинарным. По мере удаления от передней кромки, толщина ламинарного пограничного слоя увеличивается, а устой­чивость ламинарного течения уменьшается и, на некотором уда­лении, течение в пограничном слое переходит в турбулентное (рис. 12.2). При переходе ламинарного течения в турбулентное сначала происходит потеря устойчивости линий тока, они ста­новятся волнистыми (переходная зона), а затем развивается устойчивое турбулентное течение. В турбулентном пограничном слое, однако, вблизи поверхности имеется весьма тонкий под­слой, движение в котором сохраняется ламинарным. Как видно из рис. 12.3, в турбулентном слое по сравнению с ламинарным наблюдается более резкое уменьшение скорости течения у стенки.

Пограничный слой на обтекаемом теле имеет примерно ту же структуру, что и на пластине. За обтекаемым телом погранич­ные слои, образовавшиеся на нижней и верхней поверхности те­ла, смыкаются и перехо­дят в вихревой след (рис. 12.4), который по мере удаления от тела «расплывается», скорости в нем выравниваются и вдали от тела прибли­жаются к скорости невоз­мущенного потока. Решение задач погра­ничного слоя сводится в общей постановке к ин­тегрированию сложных дифференциальных урав­нений (например, уравне­ний Навье – Стокса).

Рис. 12.4. Схема потока при обтекании тела вязкой жидкостью:

1 – ламинарный слой;

2 – турбулентный слой;

3 – вихревой след;

4 – переходная зона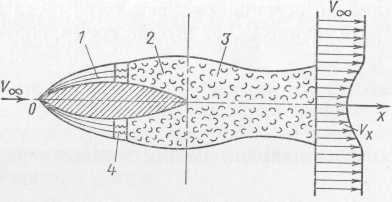

Э ти уравнения представляют собой нелинейные дифференциальные уравнения в частных производных и их интегрирование при за­данных граничных условиях сопряжено с большими математи­ческими трудностями не только в случае вязкого сжимаемого газа, но и в случае несжимаемой жидкости. Поэтому при реше­нии задач пограничного слоя приходится прибегать к упроще­нию уравнений Навье – Стокса [38], [70]. Существует ряд спосо­бов упрощения уравнений Навье – Стокса. Большой практиче­ский интерес для многих задач аэродинамики представляет, на­пример, метод Прандтля, в основу которого положено представ­ление о пограничном слое, при этом жидкость считается мало­вязкой, а скорость ее движения большой. Метод Прандтля при­годен для течений с большими числами Рейнольдса.