8.3. Основные соотношения для прямого скачка уплотнения

Рассмотрим аналитически вопрос о связи параметров газа за прямым скачком уплотнения р, q, Т, V с параметрами газа до скачка p₁ Q₁ T₁ V₁ для чего воспользуемся четырьмя урав­нениями: неразрывности, количества движения, энергии, состоя­ния.

Параметры газа при его прохождении через скачок уплотне­ния меняются скачкообразно, однако, наличие поверхностей раз­рыва не препятствует применению на скачках уплотнения ос­новных уравнений механики в интегральной форме, в частности уравнений количеств движения.

На основании закона сохранения массы уравнение неразрыв­ности (постоянства расхода) газа в сечениях до и после прямого скачка при условии постоянства площадей поперечного сечения можно записать в виде: Q₁V₁ = Q V

При пренебрежении объемными и поверхностными силами изменение количества движения газа на скачке равно импульсу сил давления, действующих по нормали к поверхности скачка, и уравнение количества движения для прямого скачка можно записать в виде p₁ – p = ρ₁V₁(V-V₁).

Поскольку при прохождении через скачок полная энергия остается неизменной (iq=const), в этом случае, считая процесс перехода газа через поверхность скачка адиабатическим и учи­тывая выражение (1.16), можно использовать уравнение энергии в виде (5.30) (8.3)

Уравнение состояния газа соответственно запишется P/n=RT. (8.4)

Уравнения (8.1), (8.2), (8.3), (8.4) являются основными урав­нениями теории прямых скачков уплотнения и выражают «усло­вия динамической совместимости» двух течений, разделенных поверхностью скачка. Таким образом, составлена система четы­рех уравнений с четырьмя неизвестными.

Прежде всего, установим связь между скоростями до и после скачка уплотнения. Используя уравнение неразрывности (8.1), запишем уравнение количества движения (8.2) в виде (8.5) или, умножая на произведение скоростей V₁V, получим . Из уравнения энергии (8.3) следует, что Подставив последние выражения в уравне­ние (8.5), после несложных преобразований получим равенство которое с учетом соотношения (7.8) приводится к так называемой формуле Прандтля VV₁= α²_кр.(8.6)

Из этой довольно простой формулы следует, что при прямом скачке уплотнения критическая скорость а_кр является средним геометрическим между скоростями до и после скачка уплотнения, т. е. в прямом скачке уплотнения всегда осуществляется пере­ход от сверхзвуковой скорости к дозвуковой.

Если перейти к скоростным коэффициентам с помощью соот­ношения (7.13), то формула Прандтля принимает еще более простой вид: λλ₁ = 1; (8.7) где λ =V/α_κρ; λ₁=V₁/α_кр.

Таким образом, при наличии неравенства V₁>V на прямом скач­ке всегда V< a_кp<V₁ или λ<1<λι. Очевидно, что в случае сверх­звукового течения перед прямым скачком уплотнения после скач­ка течение будет дозвуковым.

Соотношения для плотностей до и после скачка можно найти, используя уравнение (8.1): (8.8) или с учетом формулы (7.6): (8,9) Чтобы получить выражение для соотношения давлений до и после скачка, приведем уравнение (8.2) к виду

Учитывая, что a₁² = kp₁/Q₁, a V₁ = a₁M₁ и заменяя отношение V/V₁ его значением согласно (8.9), получим для отношения давлений выражение

(8. 10)

И мея выражение для отношений давлений (8.10) и плотнос­тей (8.9) до и после скачка, нетрудно получить выражения для отношения температур:

(8.11)

Рис. 8.11. Изменение параметров газового потока в скачке уплотнения (а — давления;

б — плотности; в — температуры) в зависимости от числа M₁.

Зависимости отношений параметров газа до и после скачка от числа Μ₁ приведены на рис. 8.11.

Определив значение Μ₁² из уравнения (8.10) и подставив его в (8.9), получим уравнение Гюгонио:

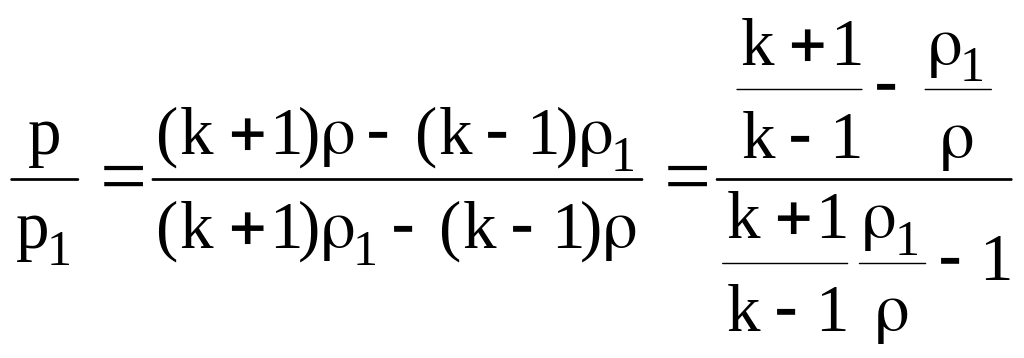(8.12) или которое устанавливает связь между отношениями плотностей и давлений до и после скачка. Подставив значение Μ₁² в (8.11), получим связь между отношениями температур и давлений да и после скачка: (8. 13)

З ависимость между параметрами состояния газа до и после скачка существенно отличается от зависимости между ними в обратимом адиабатическом процессе, характеризующимся соот­ношениями (1.22).

В изэнтропическим процессе полное давление

Рис. 8.12. Зависимость плотности газа от давле­ния при прямом скачке (1) и изэнтропическом (2) процессе.

И з сравнения процессов изменения параметров газа в скачке с обратимым адиабатическим или изэнтропическим процессом (рис. 8.12 и 8.13) следует, что при сжатии газа в скачке происходит более быстрое увеличение температуры, объяснимое необра­тимым переходом части механической энергии в тепловую, вы­зывающим дополнительный нагрев газа.

Увеличение температуры в скачке уплотнения по сравнению с изэнтропическим процессом обуславливает более медленное увеличение плотности газа за скачком при увеличении давления невозмущенного потока — кривая 1 на рис. 8.12 проходит кру­че, чем кривая, отражающая обратимый адиабатический про­цесс. Кривая 1, построенная по уравнениям (8.12), называется адиабатой Гюгонио.

Рис. 8.13. Изменение дав­ления в зависимости от температуры при изэнт­ропическом процессе (1) и прямом скачке (2)

Адиабата Гюгонио имеет вертикальную асимптоту, соответ­ствующую режиму M₁ -> ∞ или, как это следует из соотношения (8.9), режиму ρ/ρ1=(k+1)/(k – 1). Действительно, когда ско­рость перед скачком приближается к бесконечности, плотность за скачком стремится к определенному конечному пределу. Ве­личину этого предела можно определить из формулы (8.9): (8. 14)

Для воздуха (k = 1,4) этот предел равен шести. Причиной ог­раниченного увеличения плотности газа за скачком является сильный разогрев газа при прохождении его через скачок уплот­нения.

В отличие от адиабаты Гюгонио в обратимом адиабатическом процессе, описываемом уравнениями (1.22), неограниченному увеличению давления соответствует неограниченное возрастание плотности.

Отношение скоростей на скачке уплотнения в соответствии с уравнением неразрывности обратно отношению плотностей, по­этому скорость V после скачка не уменьшается до нуля при не­ограниченном увеличении M₁, а уменьшается в воздухе лишь в шесть раз.

Звуковую волну можно рассматривать как предельный слу­чай ударной волны. Из равенства (8.1) следует, что (8. 15)

Исключая из этого выражения разность скоростей с учетом уравнения (8.2), получим зависимость (8. 16) которая позволяет определять скорость распространения удар­ной волны конечной интенсивности в неподвижной среде, на­пример, скорость распространения взрывной волны.

Для прямого скачка малой интенсивности (p->p₁ и ->₁) эту зависимость можно записать в виде Таким образом, звуковая волна является бесконечно малой интенсивности.