
- •Глава 8
- •8.1. Распространение малых возмущений
- •8.2. Обтекание углов плоскопараллельным
- •8.3. Основные соотношения для прямого скачка уплотнения
- •8.4. Давление в критической точке за прямым скачком
- •8.5. Косые скачки уплотнения
- •8.6. Связь между положением фронта
- •8.8. Изменение давления при отклонении
Глава 8
МАЛЫЕ ВОЗМУЩЕНИЯ И СКАЧКИ УПЛОТНЕНИЯ В ГАЗОВОМ ПОТОКЕ
8.1. Распространение малых возмущений
Каждая точка поверхности тела, движущегося в газе, является источником повышения (или понижения) давления, плотности и других параметров газового потока. Изменение указанных параметров, вызванное движением твердого тела, называется возмущением. В механике жидкостей и газов рассматриваются малые (слабые) и конечные (сильные) возмущения. Основное отличие этих двух видов возмущений состоит в поведении параметров потока, определяющих течение. При малых возмущениях все параметры течения являются непрерывными функциями координат и времени. Скачкообразно изменяются не сами параметры газа (ρ, p, Г), а только скорости их изменения, т. е. их производные, или градиенты.
Обычно при малых возмущениях величина приращения какого-либо параметра мала по сравнению с его значением до появления возмущения. Скорость распространения малых возмущений равна местной скорости звука.
Конечные (сильные) возмущения характеризуются скачкообразным изменением на некоторых поверхностях в потоке самих параметров на конечную величину, т. е. наблюдается разрыв непрерывности изменения параметров газа.
В аэродинамике сильные возмущения называются скачками уплотнения или ударными волнами.
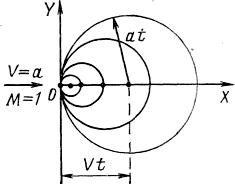
Рис. 8.1.
Р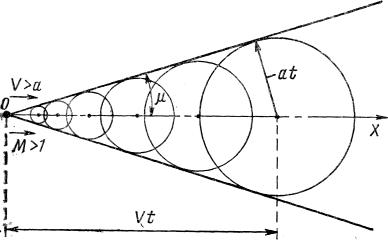 аспространение
волн от источника возмущений,
движущегося со скоростью, большей
скорости звука
аспространение
волн от источника возмущений,
движущегося со скоростью, большей
скорости звука
(при V>a образуется конус возмущений)
Рис. 8.2.
Распространение волн от источника возмущений, движущегося со скоростью звука (V=a)
Рассмотрим в сверхзвуковом газовом потоке некоторую неподвижную точку О (рис. 8.1), являющуюся источником малых возмущений. Возмущения от нее распространяются во все стороны с местной скоростью звука а в виде сферических волн уплотнения или разрежения. В неподвижной среде границей возмущенной зоны является расширяющаяся сферическая поверхность с центром в точке О. При равномерном движении среды сферические волны, возникающие в точке О, сносятся потоком в направлении скорости течения.
За время t радиус сферической волны, исходящей из возмущающей точки О, станет равным аt, а центр волны будет снесен потоком на расстояние Vt относительно этой же точки О. Волны, возникающие позднее, имеют меньший радиус и находятся ближе к центру.
При сверхзвуковом движении среды (V>a) поверхность, огибающая сферические волны, образует конус возмущений с вершиной в точке 0. Синус угла при вершине такого конуса (угла слабых возмущений), как видно на рис. 8.1, может быть представлен в виде sin μ = α∙t/V∙t = α/V = 1/M. Конус, определяемый этим условием, обычно называется характеристическим конусом, или конусом Маха. Коническая поверхность с углом раствора 2μ является границей, в пределах которой распространяются малые возмущения, идущие из точки О, и за пределы которой они не выходят.
Из выражения, определяющего конус Маха, видно, что при увеличении числа Μ угол μ уменьшается, тем самым уменьшается возмущенная зона, и наоборот при уменьшении числа Μ угол μ увеличивается, тем самым увеличивается возмущенная зона.
Когда газовый поток движется со скоростью, равной скорости распространения возмущений, исходящих из точки О (V = a, М = 1), угол μ = /2. В этом случае границей возмущения является плоскость, нормальная к направлению скорости V (рис. 8.2).
При дозвуковой скорости потока (V<at M<1) возникающие в точке О сферические волны расширяются быстрее, чем сносятся потоком, вследствие чего возмущенная зона неограниченно расширяется во все стороны относительно точки О (рис. 8.3). Таким образом, в дозвуковом потоке возмущения, возникшие в некоторой точке, распространяются на весь поток, а в сверхзвуковом потоке локализуются внутри конуса с углом раствора 2μ ≤ π.
З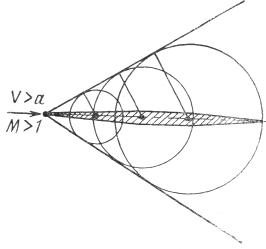 аметим,
что малые возмущения возникают также
при обтекании тонкого тела с острой
передней кромкой (рис. 8.4). При этом
поверхность, огибающая волны возмущений,
может быть цилиндрической (плоское
тело) или более сложной формы (тело
вращения и др.).
аметим,
что малые возмущения возникают также
при обтекании тонкого тела с острой
передней кромкой (рис. 8.4). При этом
поверхность, огибающая волны возмущений,
может быть цилиндрической (плоское
тело) или более сложной формы (тело
вращения и др.).
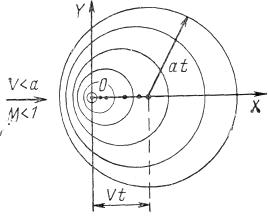
Рис 8.3.
Распространение волн от источника возмущений, движущегося с дозвуковой скоростью (V<a)
Рис. 8.4.
Распространение волн возмущений при обтекании тонкого остроконечного тела сверхзвуковым потоком
К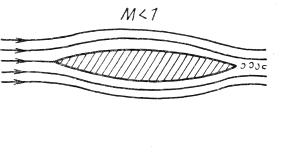
 рылья
современных скоростных самолетов,
артиллерийские снаряды и ракеты с
некоторым приближением могут
рассматриваться как тонкие тела. Спектры
обтекания заостренного тонкого профиля
под нулевым углом атаки при дозвуковых
и сверхзвуковых скоростях показаны на
рис. 8.5. При дозвуковых скоростях потока
граница возмущений находится впереди
тела на бесконечно большом расстоянии
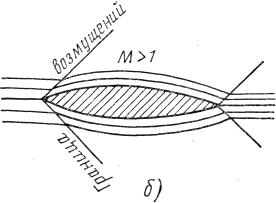
(рис. 8.5, а), при сверхзвуковых - у
самого острия тела (см. рис. 8.5, б), при
этом до границы возмущения тело не
оказывает никакого влияния на поток,
т. е. поток невозмущен.
рылья
современных скоростных самолетов,
артиллерийские снаряды и ракеты с
некоторым приближением могут
рассматриваться как тонкие тела. Спектры
обтекания заостренного тонкого профиля
под нулевым углом атаки при дозвуковых
и сверхзвуковых скоростях показаны на
рис. 8.5. При дозвуковых скоростях потока
граница возмущений находится впереди
тела на бесконечно большом расстоянии
(рис. 8.5, а), при сверхзвуковых - у
самого острия тела (см. рис. 8.5, б), при
этом до границы возмущения тело не
оказывает никакого влияния на поток,
т. е. поток невозмущен.
Рис. 8.5. Спектры обтекания тонкого профиля
при дозвуковых (а) и сверхзвуковых (б) скоростях
Любая точка потока, в которой скорость отличается от скорости соседних точек, может рассматриваться как источник возмущений, и, следовательно, как вершина характеристического конуса, ограничивающего возмущенную зону. Пересечение боковой поверхности этого конуса с плоскостью течения, проходящей через источник возмущений, дает след на плоскости течения, называемый линией возмущения.
Линия возмущения наклонна к направлению вектора скорости под углом μ=arcsin(a/V). Линия возмущения прямолинейна при слабых возмущениях и может быть криволинейной при сильных возмущениях (обтекание толстого тела сверхзвуковым потоком).
В случае обтекания сверхзвуковым потоком прямолинейной гладкой стенки, параллельной вектору скорости невозмущенного потока, течение оказывается невозмущенным. Однако в реальных условиях трудно создать идеально гладкую стенку. Наличие да же незначительных бугорков шероховатости на прямолинейной стенке или изменение кривизны твердой стенки приводят к появлению возмущений в потоке.
