Алгоритм решения ЗЛП симплекс-методом

1. Записать систему ограничений задачи с положительными свободными членами в канонической форме, то есть в виде уравнений.

2. Выделить в системе ограничений единичный базис, сохранив свободные члены положительными, то есть выполнить симплекс-преобразование.

3. Найти исходный опорный план и значение функции цели.

4. Проверить исходный план на оптимальность. Для этого необходимо вычислить значения 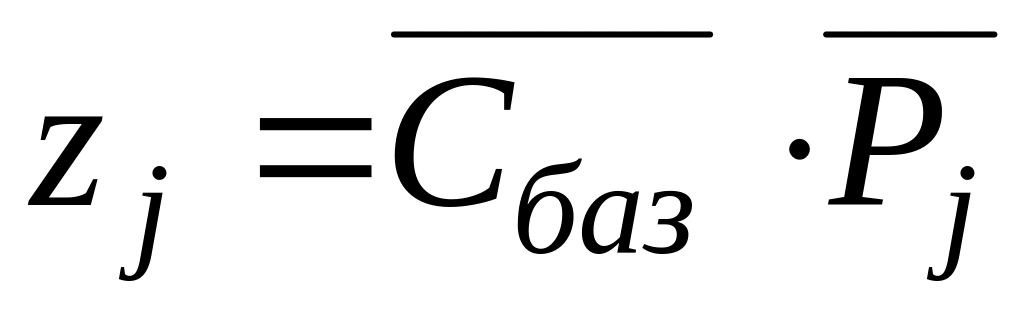и оценки .

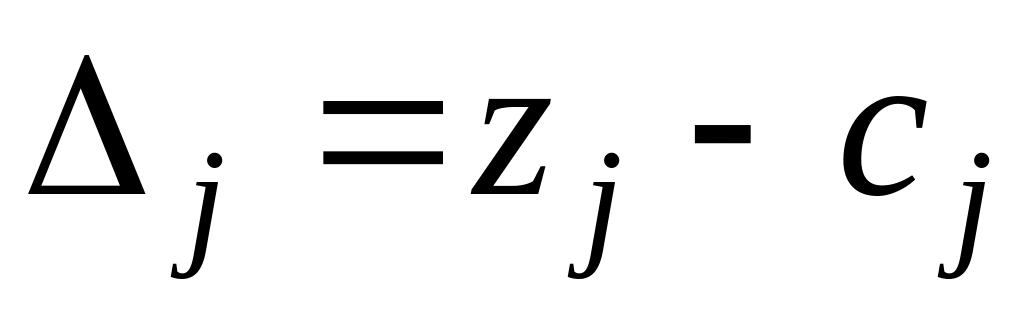Если все оценки (в случае максимизации целевой функции) или все оценки (в случае минимизации целевой функции), то исходный опорный план является оптимальным и задача решена.

Если нарушен критерий оптимальность, то есть среди оценок есть хотя бы одна отрицательная (в случае максимизации целевой функции) или положительная (в случае минимизации целевой функции), то план необходимо улучшить.

5. Улучшение исходного опорного плана:

1. если критерий оптимальности нарушен для одного 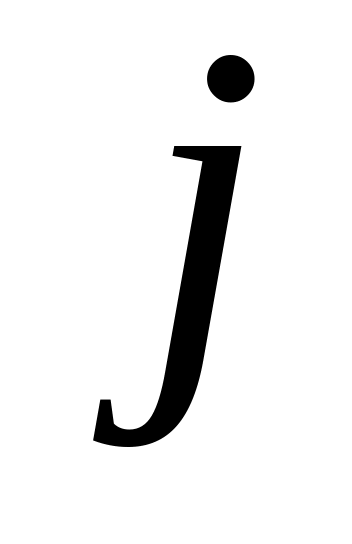-го вектора, то для него вычисляем параметр:

, где ,

и соответствующий вектор вводим в базис, используя однократное замещение базиса.

2. если критерий оптимальности нарушен для нескольких векторов, то для каждого соответствующего вектора вычисляем 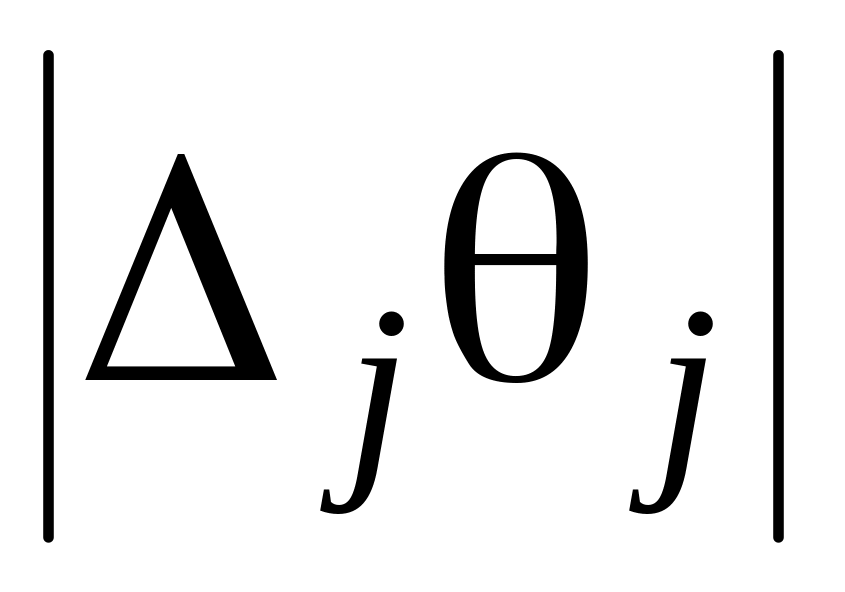и в базис вводим вектор с максимальным значением этого произведения (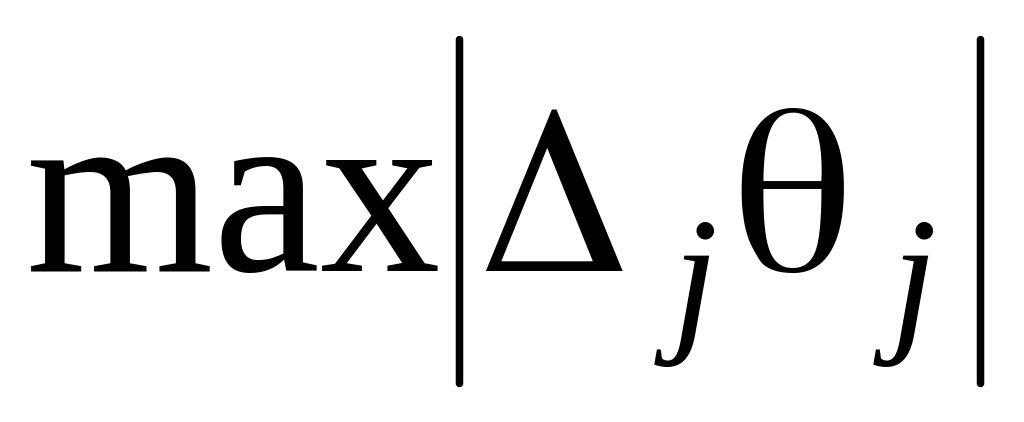 ), то есть направляющий столбец 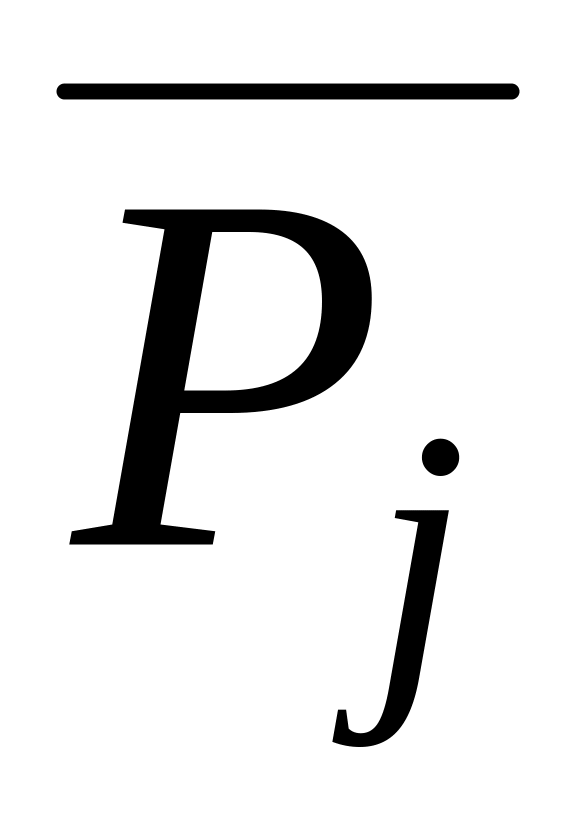определяется максимальным значением абсолютной величины произведения , а направляющая строка – минимальным отношением .

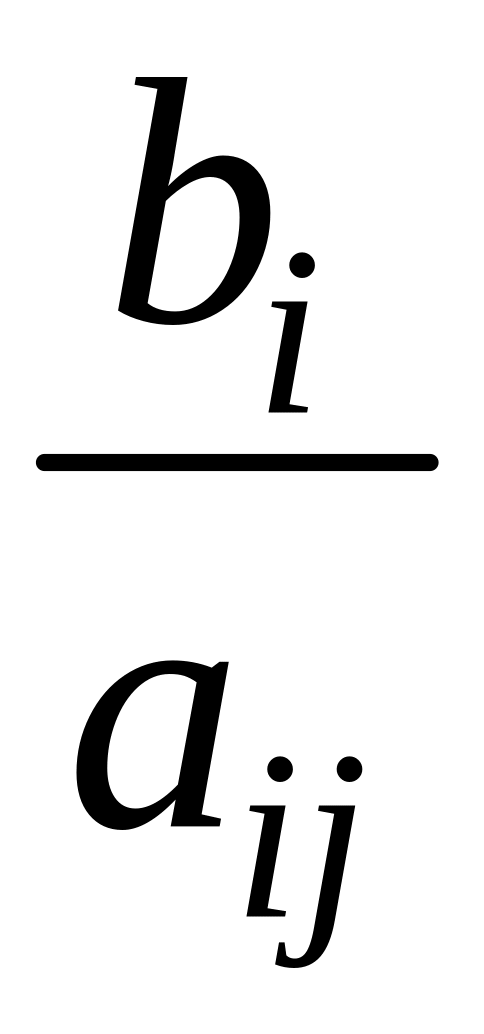6. Новый опорный план проверяем на оптимальность. Процесс продолжаем до тех пор, пока не будет выполнен критерий оптимальности.

Замечание 1: если для -го вектора нарушен критерий оптимальности, а координаты -го вектора отрицательные, то план не является оптимальным, улучшить его невозможно, ЗЛП решения не имеет.

Замечание 2 (проблема вырождения): при применении симплекс-метода монотонный рост целевой функции при исследовании на максимум (или монотонное убывание при исследовании на минимум) имеет место только тогда, когда при каждой итерации мы получаем невырожденный опорный план. Встречаются задачи, когда основная система ограничений в правой части содержит один или несколько нулей. Аналогичная ситуация может возникать и во время решения задачи.

Рассмотрим, как изменяется целевая функция, если при очередном преобразовании по методу Жордана – Гаусса разрешающий элемент содержится в строке с нулевой правой частью. Известно, что при каждой итерации целевая функция изменяется на величину . Поскольку , то введение в базис вектора, которому отвечает нулевое симплексное отношение, не сопровождается изменением целевой функции. Как правило, после нескольких преобразований с использованием нулевого симплексного отношения можно получить план, который уже был раньше, то есть симплекс-метод зацикливается.

Замечание 3: если при вычислении несколько одинаковых минимальных значений, то вычисляют вспомогательное значени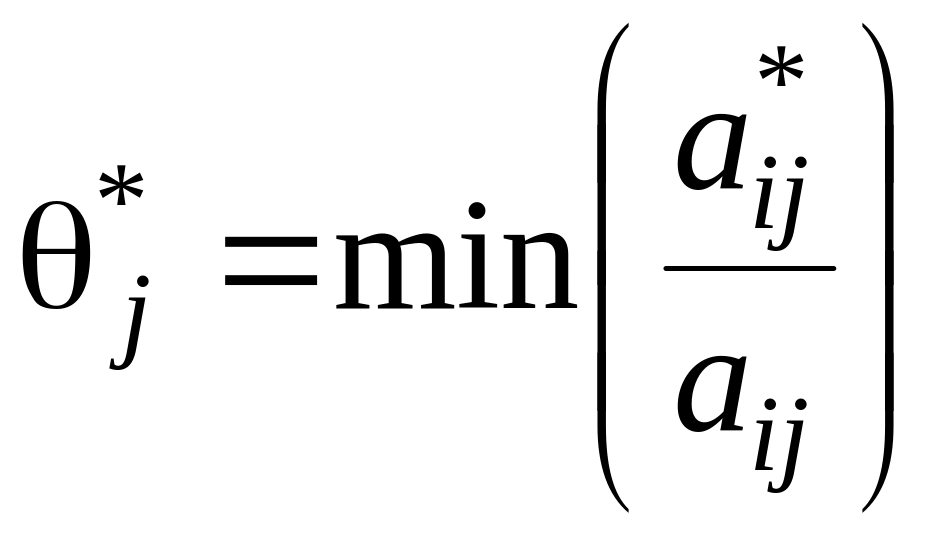е , где – координаты свободного вектора, при этом включают с учетом знака (то есть и ).

Рассмотрим это на примере.

Пусть имеем векторы в виде таблицы (табл. 38.1).

Таблица 38.1

Векторы системы ограничений злп

P0	P1	P2	P3	P4	P5	P6
6 9 30 12	–2 –1 –1 1	1 3/2 5 1	1 0 0 0	0 1 0 0	0 0 1 0	0 0 0 1

Вычислим ,

, то есть разрешающий элемент 1 в первой строке вектора .

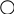
Замечание 4 (единственность решения): если план оптимальный, а некоторые оценки, соответствующие свободным векторам равны нулю ( ), то если эти векторы вводить в базис, можно получить новый оптимальный план, но значение функции цели не изменится, то есть задача имеет множество решений, их выпуклая линейная комбинация также является решением ЗЛП (геометрически, этодве угловые точки многоугольника планов и отрезок, их соединяющий, тоже является решением ЗЛП). Такое решение называется альтернативным оптимумом.

Пример 38.3.

Найти минимум функции ,

если

.

Решение.

Запишем матрицу ограничений: .

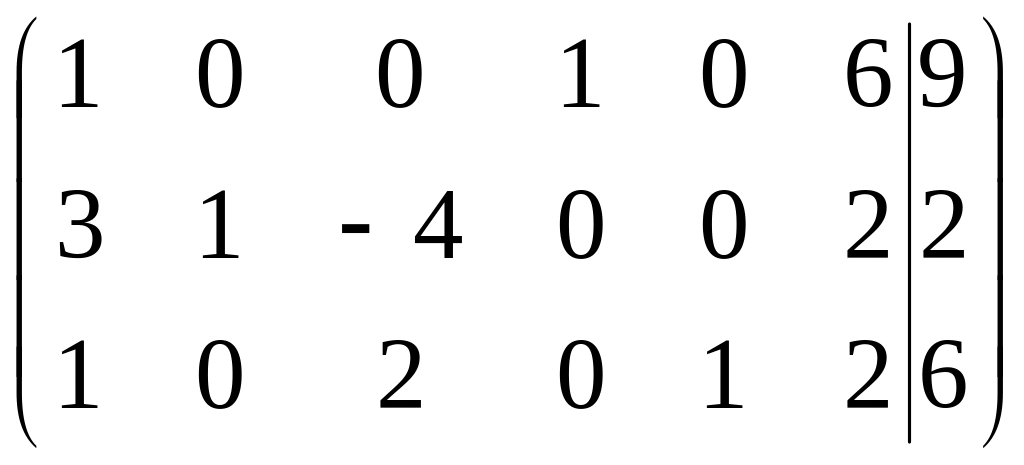Единичные векторы принимаем за базис.

Свободным переменным присваиваем значения Тогда

Следовательно, опорный план: .

Значение целевой функции: .

Проверим начальный опорный план на оптимальность. Для этого составим симплекс-таблицу (табл. 38.2).

Таблица 38.2

Симплекс- таблица (исходные данные – 1-я итерация)

Базис	Сбаз	сj	1	–1	1	1	1	–1
		P0	P1	P2	P3	P4	P5	P6
P 4 P2 P5	1 –1 1	9 2 6	1 3 1	0 1 0	0 –4 2	1 0 0	0 0 1	6 2 2
		13	–1	–1	6	1	1	6
		–	–2	0	5	0	0	7

Последняя строка табл. 38.2 показывает, что начальный план не является оптимальным, так как имеем две положительные оценки: , . Поэтому переходим к новому опорному плану. Для этого вводим в базис вектор, для которого наибольшее, где .

: так как соответствующий столбец имеет один положительный элемент, то . Тогда .

: , тогда .

Так как , то в базис вводим вектор Р₃, разрешающий элемент 2 в последней строке.

Из базиса выводим вектор P₅, у которого единица в последней строке. Составляем новую таблицу (табл. 38.3). Пояснения к ее заполнению приведены ниже.

Таблица 38.3

Симплекс- таблица (2-я итерация)

Базис	Сбаз	сj	1	–1	1	1	1	–1
		P0	P1	P2	P3	P4	P5	P6
P2 P4 P3	–1 1 1	14 9 3	5 1 ½	1 0 0	0 0 1	0 1 0	2 0 ½	6 6 1
		–2	–7/2	–1	1	1	–3/2	1
		–	–9/2	0	0	0	–5/2	2

Имеем новый базис: Р₂, Р₃, Р₄.

В столбце C_баз записаны коэффициенты при базисных неизвестных целевой функции: –1; 1; 1.

Заполняем строку вектора, который ввели в базис (Р₃). Для этого элементы третьей строки табл. 38.2 делим на разрешающий элемент 2. Получили разрешающую (ведущую) строку.

В столбце Р₃ необходимо получить единичный вектор. В первой строке табл. 38.2 имеем 0, поэтому эту строку перепишем без изменений. Во второй строке табл. 38.2 на месте элемента (–4) необходимо получить 0. Для этого каждый элемент ведущей строки табл. 38.3 умножим на 4 и прибавим к соответствующим элементам второй строки табл. 38.2.

Получим новый опорный план . Проверим его на оптимальность. Для этого следует найти оценки векторов ( ). Есть одно положительное число план не оптимальный.

Переходим к новому опорному плану. Для этого вводим в базис вектор Р₆, так как только

Находим отношение свободных членов к коэффициентам последнего столбца: , поэтому выводим из базиса вектор Р₄. Следовательно, разрешающим является столбец вектора Р₆ и строка вектора Р₄ , а разрешающим элементом является 6.

Составляем новую таблицу (табл. 38.4).

Таблица 38.4