Методические указания к выполнению контрольной работы к Задаче 1

К решению задачи 1 следует приступать , изучив раздел Статитка . Надо усвоить понятия (проекции силы на ось), (момент силы относительно точки), научиться составлять уравнения равновесия для плоской системы сил.

Пример 1. Жесткая рама ADCB имеет в точке А неподвижную шарнирную опору, в точке В – подвижную шарнирную опору на катках. Определить реакции опор А и В. Все действующие нагрузки и размеры показаны на рисунке 6.

Дано: F1=30кН, F2=10кН, α=60˚,M=20кН∙м,l=0,5 м.

Решение.

Рисунок 6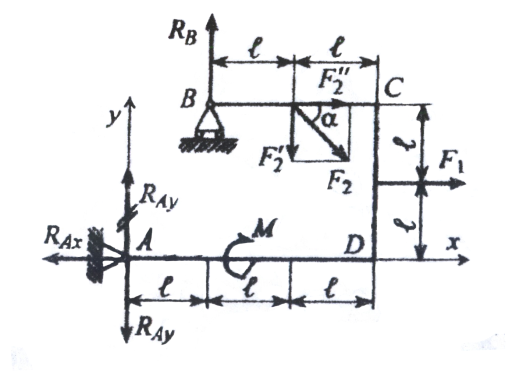

1.Заменяем связи в точках А и В их реакциями. Реакция шарнирно-неподвижной опоры А не известна по направлению, поэтому заменим ее на две составляющие: R_Ax и R_Ay. Реакция шарнирно-подвижной опоры В R_B направлена вертикально. Вместе с заданными силами получим плоскую произвольную сил. Проводим оси координат xy и составляем уравнения равновесия.

2.Для удобства расчетов разложим силу F₂ на составляющие по осям координат:

F₂’= F₂sinα =F₂sin 60˚=10∙0,87=8,7 кН

F₂’’= F₂cosα= F₂cos60˚=10∙0,5=5 кН

3.Составляем уравнение равновесия:

=0; -R_Ax + F₁+ F₂’’=0; (1)

=0; -R_Ay + R_B- F₂’=0; (2)

_A(F_i)=0; -R_Bl+F₂’∙2l+F₁l+M+ F₂’’∙2l=0. (3)

Из (3) R_{B= =} =97,4 кН.

Из (1) R_Ax=F1+ F₂’’=30+5=35кН

Из(2) R_Ay=-R_B+ F₂’=-97,4+8,7=-88,7 кН.

Так как реакция R_Ay получилась со знаком минус, значит , она направлена противоположно первоначально принятому направлению. Меняем направление на схеме и в дальнейшем расчете учитываем новое направление R_Ay .

Составляем проверочное уравнение, не использованное в решении: с=0; Rв∙ℓ-F’₂ℓ-R_AY∙3ℓ+M+R_AX∙2ℓ-F1ℓ=97,4∙2∙0,5-8,7∙0,5-88,7∙3∙0,5+20+35∙2∙0,5-30∙0,5=152,4-152,4=0

Следовательно, реакции определены верно.

Ответ:R_AX=35кН, R_AY=88,7 кН, R_B=97,4 кН.

К Задаче 2.

Задача 2 требует от студента умения строить эпюры продольных сил , нормальных напряжений и определять удлинение или укорочение бруса. Следует изучить тему “Растяжение и сжатие” в разделе “Сопротивление материалов”.

Последовательность решения задачи:

1.Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения ,в которых или приложены внешние силы, или изменяются размеры поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам .

3. Для построения эпюры нормальных напряжений определяем напряжение в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

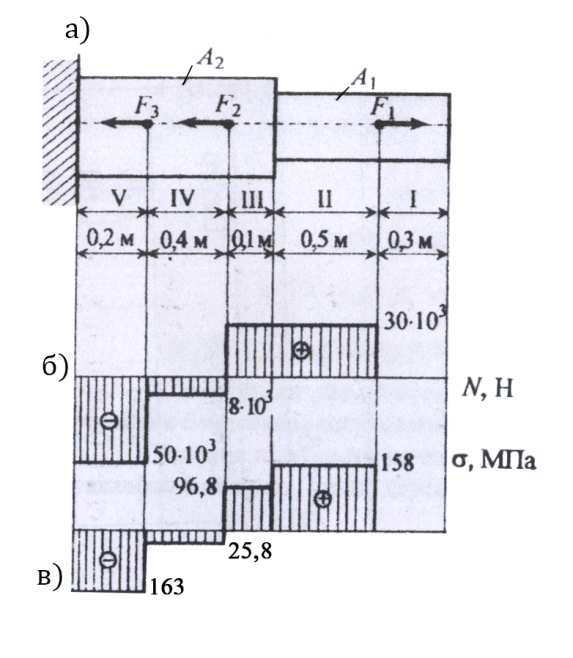
Пример 2. Для данного ступенчатого бруса (рисунок 7а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца.

Дано: F1=30кН=30∙10³ Н; F2=38кН=38∙10³ Н; F3=42кН=42∙10³ Н

А1=1,9 см²=1,9∙10² мм²; А1=3,1 см²=3,1∙10² мм²; Е=2∙10⁵ МПа

Решение

1. Отмечаем участки, как показано на рисунке 7.

2. Определяем значения продольной силы N на участках бруса:

N1=0 ; N2=F1=30 Кн; N3=F1=30кН

N4=F1-F2=-8кН N5=F1-F2-F3=-50кН.

Строим эпюру продольных сил (рисунок 7б).

Рисунок 7

3.Вычисляем значения нормальных напряжений:

σ₁ = =0;

σ₂ = = =158Н/мм²=158МПа

σ₃ = = =96,8Н/мм²=96,8 МПа

σ₄ = = =-25,8Н/мм²=25,8 МПа

σ₅ = = =-163Н/мм²=-163 МПа

Строим эпюру нормальных напряжений (рисунок 7в).

4. Определяем перемещение свободного конца бруса:

∆ℓ=∆ℓ1+∆ℓ2­­+­∆ℓ3+∆ℓ4+∆ℓ5;

∆ℓ2= 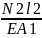= =0,394мм;

∆ℓ3= = =0,0484мм;

∆ℓ4= = =-0,0516мм;

∆ℓ5= = =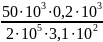-0,161мм;

∆ℓ=0,394+0,0484-0,0516-0,161=0,23 мм.

Брус удлиняется на 0,23 мм.