
- •§ 1. Уравнение непрерывности
- •§ Pvrff,
- •§ 2. Уравнение Эйлера
- •§ 3. Гидростатика
- •§ 4. Условие отсутствия конвекции
- •§ 5. Уравнение Бернулли
- •§ 6. Поток энергии
- •§ 7. Поток импульса
- •§ 8. Сохранение циркуляции скорости
- •§ 9. Потенциальное движение
- •§ 10. Несжимаемая жидкость
- •§ 12. Гравитационные волны
- •§ 13. Внутренние волны в несжимаемой жидкости
- •§ 14. Волны во вращающейся жидкости
- •Глава II
- •§ 15. Уравнения движения вязкой жидкости
- •§ 16. Диссипация энергии в несжимаемой жидкости
- •§17. Течение по трубе
- •§ 18. Движение жидкости между вращающимися цилиндрами
- •§ 19. Закон подобия
- •§ 20. Течение при малых числах Рейнольдса
- •§ 21. Ламинарный след
- •§ 22. Вязкость суспензий
- •§ 23. Точные решения уравнений движения вязкой жидкости
- •§ 24. Колебательное движение в вязкой жидкости
- •§ 25. Затухание гравитационных волн
- •Глава III
- •§ 26. Устойчивость стационарного движения жидкости
- •§ 27. Устойчивость вращательного движения жидкости
- •§ 29. Неустойчивость тангенциальных разрывов
- •§ 30. Квазипериодическое движение и синхронизация частот3)
- •§ 31. Странный аттрактор
- •§ 32. Переход к турбулентности путем удвоения периодов
- •§ 33. Развитая турбулентность
- •§ 34. Корреляционные функции скоростей
- •§ 35. Турбулентная область и явление отрыва
- •§ 36. Турбулентная струя
- •§ 37. Турбулентный след
- •§ 38. Теорема Жуковского
- •Глава IV
- •§ 39. Ламинарный пограничный слой
- •1. Определить толщину пограничного слоя вблизи критической точки (см. § 10) на обтекаемом жидкостью теле.
- •2. Определить движение в пограничном слое при конфузорном (см. § 23) течении между двумя пересекающимися плоскостями (к.. Pohlhausen, 1921).
- •§ 41. Устойчивость движения в ламинарном пограничном слое
- •2) Эта аналогия указана а в. Тимофеевым (1979) и а а Андроновым и а л. Фабрикантом (1979); ниже мы следуем изложению а. В. Тимофеева.
- •8) При V"(y) шг 0 уравнение (41,2) вообще не имеет решений, удовлетворяющих необходимым граничным условиям.
- •§ 42. Логарифмический профиль скоростей
- •§ 43. Турбулентное течение в трубах
- •§ 44. Турбулентный пограничный слой
- •§ 45. Кризис сопротивления
- •§ 46. Хорошо обтекаемые тела
- •§ 47. Индуктивное сопротивление
- •§ 48. Подъёмная сила тонкого крыла
- •S2(£)-Citt) 6-«
- •Глава V
- •§ 49. Общее уравнение переноса тепла
- •§ 50. Теплопроводность в несжимаемой жидкости
- •§ 51. Теплопроводность в неограниченной среде
- •§ 52. Теплопроводность в ограниченной среде
- •§ 53. Закон подобия для теплопередачи
- •§ 54. Теплопередача в пограничном слое
- •ВгТт « - у«р-
- •§ 55. Нагревание тела в движущейся жидкости
- •§ 56. Свободная конвекция
- •§ 57. Конвективная неустойчивость неподвижной жидкости
- •§ 58. Уравнения гидродинамики для жидкой смеси
- •§ 59. Коэффициенты диффузии и термодиффузии
- •§ 60. Диффузия взвешенных в жидкости частиц
- •Глава VII
- •§ 61. Формула Лапласа
- •§ 62. Капиллярные волны
- •§ 63. Влияние адсорбированных пленок на движение жидкости
- •Глава VIII
- •§ 64. Звуковые волны
- •§ 66. Энергия и импульс звуковых волн
- •§ 66. Отражение и преломление звуковых волн
- •§ 67. Геометрическая акустика
- •§ 68. Распространение звука в движущейся среде
- •§ 69. Собственные колебания
- •§ 70. Сферические волны
- •§71. Цилиндрические волны
- •§ 72. Общее решение волнового уравнения
- •Ctjc42-(X-q2- (*/-г,)2'
- •§ 73. Боковая волна
- •§ 74. Излучение звука
- •§ 75. Возбуждение звука турбулентностью
- •V 1г' 4я j дхидх1к
- •§ 76. Принцип взаимности
- •§ 77. Распространение звука по трубке
- •§ 78. Рассеяние звука
- •§ 79. Поглощение звука
- •4. Определить дополнительное поглощение звука, распространяющегося в смеси двух веществ, связанное с диффузией (и. Г. Шапошников и 3. А Гольдберг, 1952).
- •§ 80. Акустическое течение
- •§ 81. Вторая вязкость
- •Глава IX
- •§ 82. Распространение возмущений в потоке сжимаемого газа
- •2) Во избежание недоразумений оговорим, что если перед обтекаемым телом возникает ударная волна, то эта область несколько увеличивается (см. § 122).
- •§ 83. Стационарный поток сжимаемого газа
- •§ 84. Поверхности разрыва
- •§ 85. Ударная адиабата
- •2) Такой выбор системы координат будет подразумеваться везде в этой главе, за исключением § 92.
- •§ 86. Ударные волны слабой интенсивности
- •§ 87] Направление изменения величин в ударной волне 463
- •§ 87. Направление изменения величин в ударной волне
- •§ 88. Эволюционность ударных волн
- •§ 89. Ударные волны в политропном газе
- •1. Получить формулу
- •§ 90. Гофрировочная неустойчивость ударных волн
- •2) Сравните с аналогичной ситуацией для тангенциальных разрывов — задача 2 § 84.
- •1) Эта неустойчивость тоже была указана с. П. Дьяковым (1954); правильное значение нижней границы в (90,17) найдено в. М. Конторовичем (1957).
- •§ 91. Распространение ударной волны по трубе
- •§ 92. Косая ударная волна
- •§ 93. Ширина ударных волн
- •§ 94. Ударные волны в релаксирующей среде
- •§ 96. Слабые разрывы
- •Глава X
- •§ 97. Истечение газа через сопло
- •§ 98. Вязкое движение сжимаемого газа по трубе
- •§ 99. Одномерное автомодельное движение
- •5. Определить движение в изотермической автомодельной волне разрежения.
- •§ 100. Разрывы в начальных условиях
- •§ 101. Одномерные бегущие волны
- •§ 102. Образование разрывов в звуковой волне
- •§ 103. Характеристики
- •§ 104. Инварианты Римана
- •§ 105. Произвольное одномерное движение сжимаемого газа
- •§ 106. Задача о сильном взрыве
- •§ 107. Сходящаяся сферическая ударная волна
- •2) Эта задача была рассмотрена независимо Гудерлеем (о. Guderleu, 1942) и л. Д. Ландау и к. П. Станюковичем (1944, опубликовано в 1955).
- •§ 108. Теория «мелкой воды»
- •Глава XI
- •§ 109. Волна разрежения
- •§ 111. Пересечение ударных волн с твердой поверхностью
- •§ 112. Сверхзвуковое обтекание угла
- •§ 113. Обтекание конического острия
- •Глава XII
- •§ 114. Потенциальное движение сжимаемого газа
- •§ 115. Стационарные простые волны
- •§ 116. Уравнение Чаплыгина (общая задача
- •§ 117. Характеристики плоского стационарного течения
- •§ 118. Уравнение Эйлера — Трикоми. Переход через звуковую скорость
- •§1191 Решение уравнения эйлера —трикоми 619
- •§ 119. Решения уравнения Эйлера — Трикоми вблизи неособых точек звуковой поверхности
- •§ 120. Обтекание со звуковой скоростью
- •§ 121. Отражение слабого разрыва от звуковой линии
- •Глава XIII
- •§ 122. Образование ударных воли при сверхзвуковом обтекании тел
- •§ 123. Сверхзвуковое обтекание заостренного тела
- •§ 124. Дозвуковое обтекание тонкого крыла
- •§ 125. Сверхзвуковое обтекание крыла
- •§ 126. Околозвуковой закон подобия
- •§ 127. Гиперзвуковой закон подобия
- •Глава XIV
- •§ 128. Медленное горение
- •§ 129. Детонация
- •§ 130. Распространение детонационной волны
- •§ 131. Соотношение между различными режимами горения
- •§ 132. Конденсационные скачки
- •Глава XV
- •§ 133. Тензор энергии-импульса жидкости
- •§ 134. Релятивистские гидродинамические уравнения
- •§ 135. Ударные волны в релятивистской гидродинамике
- •§ 136. Релятивистские уравнения движения вязкой и теплопроводной среды
- •§ 137. Основные свойства сверхтекучей жидкости
- •§ 138. Термомеханический эффект
- •§ 139. Уравнения гидродинамики сверхтекучей жидкости
- •§ 140. Диссипативные процессы в сверхтекучей жидкости
- •§ 141. Распространение звука в сверхтекучей жидкости
§ 92. Косая ударная волна
Рассмотрим стационарную ударную волну, отказавшись при этом от подразумевавшегося везде выше выбора системы координат, в которой скорость газа направлена перпендикулярно к данному элементу поверхности волны. Линии тока могут пересекать поверхность такой ударной волны наклонно, причем пересечение сопровождается преломлением линий тока. Касательная составляющая скорости газа не меняется при прохождении через ударную волну, а нормальная составляющая согласно (87,4) падает:
Vu = V2t, f l/i > V2n.
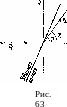
Поэтому ясно, что при прохождении через ударную волну линии тока приближаются к ней (как это показано на рис. 63). Таким образом, преломление линий тока на ударной волне происходит всегда в определенном направлении.
Выберем направление скорости vi газа перед ударной волной в качестве оси х, и пусть ср — угол между поверхностью разрыва и осью х (рис. 63). Возможные значения угла ср ограничены лишь условием, чтобы нормальная составляющая скорости vi
') Выражение (91,7) для произвольной (не политропной) среды и его связь с условиями гофрировочной неустойчивости ударных волн указаны С. Г. Су гаком и В. Е. Фортовым, А. Л, Ни (1981).
превышала скорость звука с\. Поскольку Vi„ = v sin ф, то отсюда следует, что ф может иметь произвольные значения в интервале между я/2 и углом Маха оц:
а, < ф < л/2, sin cci = c\/v\ = 1/Mi.
Движение позади ударной волны может быть как до-, так и сверхзвуковым (меньше скорости звука с2 должна быть лишь нормальная компонента скорости); движение же перед ударной
 волной
—
непременно
сверхзвуковое.
Если
движение
газа
по
обе
стороны
от
ударной
волны
является
сверхзвуковым,
то
все
возмущения
могут
распространяться
вдоль
ее
поверхности
лишь
в
ту
сторону,
ку-х
да
направлена
касательная
к
ней
составляющая
скорости
газа.
В
этом
смысле
можно
говорить
о
«направлении»
ударной
волны
и
различать
по
отношению
к
какому-либо
месту
«исходящие»
из
него
и
«приходящие»
волны
(подобно
тому
как
мы
это
уже
делали
для
характеристик,
вокруг
которых
движение
всегда
является
сверхзвуковым;
см.
§
82).
Если
же
движение
позади
ударной
волны
является
дозвуковым,
то
понятие
о
ее
направлении
теряет,
строго
говоря,
смысл,
так
как
возмущения
могут
распространяться
вдоль
ее
поверхности
во
все
стороны.
волной
—
непременно
сверхзвуковое.
Если
движение
газа
по
обе
стороны
от
ударной
волны
является
сверхзвуковым,
то
все
возмущения
могут
распространяться
вдоль
ее
поверхности
лишь
в
ту
сторону,
ку-х
да
направлена
касательная
к
ней
составляющая
скорости
газа.
В
этом
смысле
можно
говорить
о
«направлении»
ударной
волны
и
различать
по
отношению
к
какому-либо
месту
«исходящие»
из
него
и
«приходящие»
волны
(подобно
тому
как
мы
это
уже
делали
для
характеристик,
вокруг
которых
движение
всегда
является
сверхзвуковым;
см.
§
82).
Если
же
движение
позади
ударной
волны
является
дозвуковым,
то
понятие
о
ее
направлении
теряет,
строго
говоря,
смысл,
так
как
возмущения
могут
распространяться
вдоль
ее
поверхности
во
все
стороны.
Выведем соотношение, связывающее друг с другом две компоненты скорости газа после его прохождения через косую ударную волну; при этом будем предполагать газ политропным.
Непрерывность касательной к волне составляющей скорости означает, что v\ cos ф = v2x cos ф + viu sin ф, или
tgop-.
Ol — V2X
(92,1)
Далее, воспользуемся формулой (89,6); в этой формуле Vi и i>2 обозначают нормальные к плоскости ударной волны составляющие скорости и должны быть теперь заменены на vi sin ф и v%x sin ф — V2y cos ф, так что имеем:
уц gjnФ — v2y cos.cp _ у — 1 "-2
2с1
Y+1
(92,2)
t), sin ф
Из двух написанных соотношений можно исключить угол ф. После простых преобразований получим следующую формулу,
определяющую связь между v2x и v2y (при заданных v\ и С\)
(92,3)
2—G- -^)-^-v
Vly = (Vl - V2xf
Y+ 1 0|
Этой формуле можно придать более изящный вид, если ввести в нее критическую скорость. Согласно уравнению Бернулли и определению критической скорости имеем:
У+1
2
(V
— 1)
Т +
с:
■v2 + -
Y+ 1 1 Y+ 1 Введя эту величину в (92,3), получим:
(92,4)
Чу = (»1 - 4xf
Y-+ 1
viv2X -«;
■»1 - vl°ix + с1
(92,5)
 Уравнение
(92,5)
называют
уравнением
ударной
поляры {A.
Busemann,
1931).
На
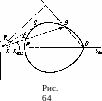
рис.
64
изображен
график
этой
зависимости;
это
есть
кривая
третьего
порядка
(так
называемая
\
строфоида
или
декартов
лист).
Она
пересекает
ось
абсцисс
в
точках
Р
и
Q
(рис.
64),
соответствующих
значениям
v2x
=
c;/rj
и
v2x
=
vii).
Проведя
из
начала
о
координат
луч
(ОВ
на
рис.
64)
под
углом
х
к
оси
абсцисс
по
длине
его
отрезка
до
точки
пересечения
с
кривой
ударной
поляры,
мы
определяем
скорость
газа
за
скачком,
поворачивающим
поток
на
угол
%.
Таких
точек
пересечения
имеется
две
(А
и
В),
т.
е.
заданному
значению
х
отвечают
две
различные
ударные
волны.
Направление
ударной
волны
тоже
может
быть
Уравнение
(92,5)
называют
уравнением
ударной
поляры {A.
Busemann,
1931).
На
рис.
64
изображен
график
этой
зависимости;
это
есть
кривая
третьего
порядка
(так
называемая
\
строфоида
или
декартов
лист).
Она
пересекает
ось
абсцисс
в
точках
Р
и
Q
(рис.
64),
соответствующих
значениям
v2x
=
c;/rj
и
v2x
=
vii).
Проведя
из
начала
о
координат
луч
(ОВ
на
рис.
64)
под
углом
х
к
оси
абсцисс
по
длине
его
отрезка
до
точки
пересечения
с
кривой
ударной
поляры,
мы
определяем
скорость
газа
за
скачком,
поворачивающим
поток
на
угол
%.
Таких
точек
пересечения
имеется
две
(А
и
В),
т.
е.
заданному
значению
х
отвечают
две
различные
ударные
волны.
Направление
ударной
волны
тоже
может
быть
') От точки Q, являющейся двойной точкой кривой, строфоида в действительности продолжается еще. в виде двух уходящих к бесконечным \v2y\ ветвей (не изображенных на рис. 64) с общей вертикальной асимптотой
Ds* —«?M + 2«»,/(Y + 1)
Однако точки этих ветвей не имеют физическою смысла: они дали бы для v2x, vzy значения, при которых v2nlv\n > 1, что невозможно.
сразу определено графически по этой же диаграмме — оно определяется перпендикуляром, опущенным из начала координат на прямую, проведенную из точки Q соответственно через точку В или А (на рис. 64 изображен угол ср для волны, соответствующей точке В). При уменьшении % точка А приближается к точке Р, отвечающей прямому (ср = л/2) скачку с v2 = cl/vi- Точка же В приближается при этом к точке Q, причем интенсивность ударной волны (скачок скорости в ней) стремится к нулю; в пределе, в самой точке Q, угол ср равен, как и следовало, углу Маха ат (угол наклона касательной к поляре к оси абсцисс в этой точке равен я/2 + ai).
Из диаграммы ударной поляры сразу можно вывести важное заключение, что угол отклонения % потока в ударной волне не может превышать некоторого максимального значения %тах, соответствующего луч>, проведенному из точки О касательно к кривой, хтах является, конечно, функцией числа Mi = v\/c\\ мы не приводим ее здесь ввиду ее громоздкости. При Mi = 1 имеем Хтах = 0, а при возрастании Mi угол хтах монотонно растет и при Mi->-сю стремится к конечному пределу. Легко рассмотреть оба предельных случая.
Если скорость V\ близка к с», то вместе с ней близка к с» и скорость v2, а угол % мал; уравнение ударной поляры (92,5) можно тогда приближенно переписать в виде')
X2 = JT3i (у 1 - у2)2 (»1 + Щ - 2с.) (92,6>
(ввиду малости угла % здесь положено v2x та v2, v2y ж с*%). Отсюда элементарным путем найдем2):
= lVY±I^ _ Л3/2= 2?/2 (М, _ П3/2 m 7у Хтах- 3з/2 Ц l) g3/2(Y+1)lMl U ' (»47>
В обратном предельном случае, при Mi -*- со, ударная поляра вырождается в окружность
Легко видеть, что при этом
Хтах = arcsi-n(l/y). (92,8)
1) Можно
легко убедиться в том, что уравнение
(92,6) будет справедли-
вым и для любого
(не политропного) газа, если только
заменить в нем ве-
личину (у + 1)/2 на
параметр а», определенный согласно
(102,2).
2) Отметим,
что эта зависимость /щах
от
Mj
—
1 находится в согласии с
общим законом
подобия (126,7) для околозвуковых течений.
предельное значение %тах(°°) = 45,6° (верхняя кривая на рисунке— аналогичный график для обтекания конуса; см. § 113).
50
30'
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р\П£*-" |
|
|
|
|
|
|
|
|
|
|
|
|
20
Окружность V2 — с* пересекает ось абсцисс между точками Р и Q (рис. 64) и поэтому делит ударную поляру на две ,части, соответствующие до- и сверхзвуковым скоростям газа позади разрыва. Точка пересечения окружности V2 = с* с полярой лежит пра- во* вее точки С, но очень близко к ней; поэтому весь участок РС соответствует переходам к дозвуковым скоростям, а участок CQ (за исключением лишь очень небольшого участка вблизи точки С) — переходам к сверхзвуковым скоростям. /,Изменения давления и плотно- сти в косой ударной волне зависят иуп t.s 2.0 г$ До з$м, только от нормальных к ней ком- понент скорости. Поэтому отноше- • 6 ния р2/р\ и p2/pi при заданных Mi
(92,9)
(92,10)
Р2-Р1
Pi
2(М2 sin2 ф — l)]
(Y — 1)М2 sin* ф-г-2
Эти отношения монотонно возрастают при увеличении угла ф от значения ф = а\ (когда р2/р\ == Рг/pi = 1) до я/2, т. е. по мере перемещения по ударной поляре от точки Q к точке Р.
Приведем еще, для справок, формулу, выражающую угол поворота % скорости через число Mi и угол ф:
ctg
% = tg ф £
(Y+l)Mf
2(М28ш2ф- l)
(92,11)
и формулу, определяющую число М2 = v2/c2 по Mi и ф|
2уМ2
sin2
ф
■
2М2
cos2
ф
(Y-1) 2 + (Y-l)M2sin2?
(92,12)
(при ф = я/2 последнее выражение переходит в (89,9)).
Две ударные волны, определяемые ударной полярой для заданного угла поворота скорости, называют волнами слабого и сильного семейства. Ударная волна сильного семейства (участок РС поляры) обладает большей интенсивностью (большим отношением p2/pi), образует больший угол ф с направлением скорости vi и превращает течение из сверх- в дозвуковое. Волна же слабого семейства (участок QC поляры) обладает
меньшей
интенсивностью,
наклонена
к
потоку
под
меньшим
углом
и
почти
всегда
оставляет
течение
сверхзвуковым.
Для
иллюстрации
на
рис.
66
изображены
зависимости
угла
%
отклонения
скорости
от
угла
ср
наклона
поверхности
разрыва
для
воздуха
(у
=
1,4)
при
нескольких
различных
значениях
числа
Мь
в
том
числе
для
предела
Mi->-oo.
Ветви
кривых,
изображенные
сплошными
линиями,
отвечают
ударным
волнам
сла-
1
t
V.
\V
\ \
ЯК
М2=7-
.
\z=
\
\
\ \
\\\
7/ 'у
/
|~"~"-ч
\ \
-*-г* 4
7
!
\
\
\ \
\i
/
/
j
i
о/
\ \
^ч
ч \
'Л \*
41
1,6/
''4/
\
\ л \
~^ч ч
т
1
1
i
/
/
\,2,
чЧ
~~
45'
40'
35°
30е
25'
20е
10°
20° 30° 40°
50°
60° Угол
наклона
ударной
волны
f
Рис.
66
80°
SO"
70°
бого
семейства,
а
изображенные
пунктиром
—
ударным
волнам
сильного
семейства.
Пунктирная
линия
%
= хтах
—
геометрическое
место
точек
максимального
(при
каждом
заданном
Mi)
угла
отклонения,
а
сплошная
линия
М2
= 1
разделяет
области
сверх-и
дозвукового
течения
позади
разрыва;
узкая
область
между
этими
двумя
линиями
отвечает
ударным
волнам
слабого
семейства,
превращающим,
однако,
течение
из
сверх-
в
дозвуковое.
Разность
значений
угла
ср
на
линиях
%
=
хтах
и
М2
= 1
(при
заданном
Mi)
нигде
не
превышает
4,5°;
разность
же
между
^тах
и
значением
%
—
%зв
на
линии
М2
= 1
(тоже
при
заданном
Mi)
не
превышает
0,5°').
')
Подробные графики и диаграммы, относящиеся
к
ударной
поляре (для у
=
1,4) можно найти в книгах: Липман
Г.
В.,
Рошко
А.
Элементы
газовой динамики. — М.: ИЛ, 1960. [Liepmann
Н.
W.,
Roshko
A.
Elements
of gas dynamics. —
N. Y.:
J. Wiley, 1957];
Oswatitsch
K-
Gas
dynamics. —
N. Y.:
Academic Press, 1956.
