4. Определить дополнительное поглощение звука, распространяющегося в смеси двух веществ, связанное с диффузией (и. Г. Шапошников и 3. А Гольдберг, 1952).

Решение. В смеси имеется дополнительный источник поглощения звука, связанный с тем, что возникающие в звуковой волне градиенты температуры и давления приводят к появлению необратимых процессов термо- и бародиф-фузии (градиента же массовой концентрации, а с ней и чистой диффузии, очевидно, не возникает). Это поглощение определяется членом

в скорости изменения энтропии (59,13) (мы обозначим здесь концентрацию посредством С в отличие от скорости звука с). Диффузионный поток

с k„ из (59,10). Вычисление, аналогичное произведенному в тексте, с исполь­зованием ряда соотношений между производными термодин<"-¹"'егк1тх чин приводит к следующему результату: к выражению (79,6) для фициента поглощения добавляется член

Yd

Da²

р. т

5. Определить эффективное сечение поглощения звука шариком, радиус которого мал по сравнению с Vv/ш.

в согласии с (52,15). В случае же к>% > с² получается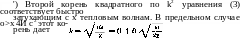

Решение. Полное поглощение складывается из эффектов вязкости и теплопроводности газа. Первый определяется работой стоксовой силы трения при обтекании шарика движущимся в звуковой волне газом (как и в за­даче 3 § 78, предполагается, что шарик не увлекается этой силой). Второй эффект определяется количеством тепла <?, передаваемым в единицу времени от газа шарику (задача 3 § 78): диссипация энергии при передаче тепла q при разности температур V между газом (вдали от шарика) и шариком равна qf'IT. Для суммарного эффективного сечения поглощения получается выражение

_e_i=L[₃v + 2_X(4e.-i)].

§ 80. Акустическое течение

Одно из самых интересных проявлений влияния вязкости на звуковые волны состоит в возникновении стационарных вихре­вых течений в стоячем звуковом поле при наличии твердых пре­пятствий или ограничивающих его твердых стенок. Это движе­ние (его называют акустическим течением) появляется во вто­ром приближении по амплитуде волны; его характерная особен­ность состоит в том, что скорость движения в нем (в простран­стве вне тонкого пристеночного слоя) оказывается не завися­щей от вязкости, — хотя самим своим возникновением оно обя­зано именно вязкости (Rayleigh, 1883).

Свойства акустического течения наиболее типичным образом проявляются в условиях, когда характерная длина задачи (раз­меры препятствий или области движения) малы по сравнению с длиной звуковой волны X, но в то же время велики по сравне­нию с введенной в § 24 глубиной проникновения вязких волн б = у 2v/co:

Х>/>6. (80,1)

Ввиду последнего условия, в области движения можно выде­лить узкий акустический пограничный слой, в котором происхо­дит падение скорости от ее значения в звуковой волне до нуля на твердой поверхности. Поскольку скорость газа в этом слое (как и в самой звуковой волне) мала по сравнению со скоростью звука, а его характерный размер — толщина б — мал по сравне­нию с а (ср. условие (10,17)), то движение в нем можно рас­сматривать как несжимаемое.

Рассмотрим акустический пограничный слой у плоской твер­дой стенки (плоскость xz), причем движение будем считать пло­ским — в плоскости ху (Н. Schlichting, 1932). Приближения, связанные с малой толщиной пограничного слоя, описаны в § 39 и сохраняют силу для рассматриваемого нестационарного дви­жения. Нестационарность приводит лишь к появлению в урав­нении Прандтля (39,5) членов с производными по времени:

(производная dp/dx выражена через скорость U(x,t) течения вне пограничного слоя с помощью уравнения (9,3)). В данном случае

U = v_Q cos kx • cos at = v_Q cos kx • Re е~^ш (80,3)

(/г = ю/с), что соответствует стоячей плоской звуковой волне с частотой со. Искомую скорость v в пограничном слое выразим через функцию тока ф(л;, у, t) согласно

dip дф

^Vx~~dy' ^Vy~ дх~'

чем автоматически удовлетворяется уравнение непрерывности (39,6).

Будем решать уравнение (80,2) последовательными прибли­жениями по малой величине vo — амплитуде колебаний скорости газа в звуковой волне. В первом приближении пренебрегаем квадратичными членами полностью. Решение уравнения

удовлетворяющее требуемым условиям при у = 0 и у = со, есть ₀<1) ₌ R_e |_{0q cos} ^ . _е-ш (\ _ e-*v)},

где

Соответствующая функция тока (удовлетворяющая условию фО> = 0 при у — 0, эквивалентному условию ^о(„^{1) =} 0) есть

^) = ile{v_Qcoskx • g^l)(y)e-^lb,t}, (80,5)

В следующем приближении пишем v = v⁽¹⁾ + v⁽²> и для ско­рости v^(2> получаем из (80,2) уравнение

3t><²> d²vf dU to™ dv«>

~ЬЧ ^v ~bY~ ^{= U} ~~E7 ~ ^v* ~ЬЧ -af ■ ⁽⁸°'⁶⁾

В правой стороне имеются члены с частотами © + (0 = 2(0 и © — ю = 0. Последние приводят к появлению в v⁽²⁾ не завися­щих от времени членов, которые и описывают интересующее нас стационарное движение; ниже мы будем понимать под v⁽²⁾ только эту часть скорости. Соответствующую часть функции тока пишем в виде

^=—sm2kx-^{y) (80,7)

и для функции £⁽²⁾(#) находим уравнение

6²ф<²>'" = 1 - 11 f + 1 Re (&r £<>>"), (80,8)

где штрихи рзначают дифференцирование по у.

Решение этого уравнения должно удовлетворять условиям £^<2)(0) = 0, £^(2)/(0) = 0> эквивалентным требованию v^{2) = v^{2) — О на твердой поверхности. Что же касается условий вдали от стен­ки, то можно лишь потребовать, чтобы скорость v^{2) стремилась к конечному значению (но не к нулю). Подстановка (80,5) в (80,8) и двукратное интегрирование приводят к следующему ре­зультату для производной £^(2)/:

£<²>' (у) = 1 _ 1 е~²У'^й - e-yi⁶ sin -| - -\ е-ш* cos -| +

+ 4^^/e(cos|-sin|).

При у-*~оо она стремится к значению

£<2>'(со) = 3/8, (80,9)

чему отвечает скорость

За²,

о« (оо) = sin 2kx. (80,10)

Этот результат демонстрирует указанное в начале параграфа явление. Мы видим, что вне пограничного слоя возникает (во втором приближении по vo) стационарное движение, скорость ко­торого не зависит от вязкости. Ее значение (80,10) служит гра­ничным условием при определении акустического течения в ос­новной области движения (см. задачу)¹).

Задача

Определить акустическое течение в пространстве между двумя плоско­параллельными стенками (плоскости у = 0 и y = h), в котором имеется стоячая звуковая волна (80,3). Расстояние h между плоскостями (играющее роль характерной длины /) удовлетворяет условиям (80,1) (Rayleigh, 1883).

') Поперечная скорость, отвечающая продольной скорости (80,9), есть ^vf = ~-ycos2kx<_VM

При решении задачи о движении вне пограничного слоя эта скорость воз­никает автоматически в силу уравнения непрерывности, если поставить гра­ничное условие о^' = 0 при у = 0.

²) Другими словами, отношение v₀/c предполагается малым по сравнению со всеми другими малыми параметрами задачи; в частности, v₀U<g_6lh.

Решение. Ввиду малости скорости и⁽²> искомого стационарного дви­жения по сравнению со скоростью звука, его можно считать несжимаемым. ■Более того, ввиду предполагаемой сколь угодной малости скорости Vo в зву-ковой волне (а вместе с ней и скорости v^y ~ ^vo/c)< ^в уравнении движения можно пренебречь квадратичными членами²). Тогда уравнение (15,12) для

функции тока сводится к уравнению

⁴V»-(£+&)>-

'(отметим, что оно возникает из члена с вязкостью, но сама вязкость из него выпадает). Ищем ф^<2) в виде (80,7). Ввиду условия Л < А производные по у велики по сравнению с производными по х; пренебрегая последними, получим для функции £⁽²⁾(#) уравнение

£<²>""=0. (1)

Ввиду очевидной симметрии задачи, течение симметрично относительно плоскости (/•= Л/2. Это значит, что

(*, у) = vf (х, Л - у), vf (х, у) = - vf (х, Л - у),

для чего должно быть

£⁽²⁾ (у) = - £^(2> (А - у)-

Таким решением уравнения (1) является

--*-) +'('ЧУ-

Постоянные А и В определяются граничными условиями

£^<2) (0) = 0, f-^y (0) = 3/8. В результате находим для функции тока выражение

Ч> ' = s n 26* — [у Н s ,

16с L V 2 J (Л/2)² Г

а из него следующие окончательные формулы для распределения скоростей1

(2) ^3ао _пь Г, 3(г/-Л/2)²]

о*' = sin 2kx 1 5 ,

* 16с L (Л/2)² J

Зо²й Г/ Л\ (у - А/2)³ 1

о,7 = ^cos 2kx i i у i s— i.

" 8c IV 2 ) (h/2)² J

Скорость v*® меняет знак на расстоянии (Л/2) (l — 3^-1/2) = 0,423Л/2 от стенки.

Описываемое этими формулами течение состоит из двух рядов вихрей, симметрично расположенных относительно серединной плоскости у = Л/2 и периодичных вдоль осп х с периодом Х/2.