ВгТт « - у«р-

На расстояниях же г < ?vo имеем В_Тт °° г², а членом В,тт можно пренебречь; тогда

Brr » -g- r*q>.

§ 55. Нагревание тела в движущейся жидкости

Термометр, погруженный в неподвижную жидкость, показы­вает температуру, равную температуре жидкости. Если же жид­кость движется, то термометр покажет температуру несколько более высокую. Это обусловливается нагреванием благодаря внутреннему трению тормозящейся у поверхности термометра жидкости.

Общую задачу можно сформулировать следующим образом. Тело произвольной формы погружается в движущуюся жид­кость; по истечении достаточного промежутка времени устано­вится некоторое тепловое равновесие и требуется определить возникающую при этом разность температур Ty=zT_Q между ними.

Решение этой задачи определяется уравнением (50,2), в кото­ром, однако, теперь уже нельзя пренебречь членом, содержащим вязкость, как это было сделано в (53,1); именно этот член опре­деляет интересующий нас здесь эффект. Таким образом, для установившегося состояния имеем уравнение

v / dv. dv. \² *vr-xAT + -^(-_a£ + -₅£).

(55,1)

К нему должны быть присоединены уравнения движения (53,3) самой жидкости и, строго говоря, еще и уравнение теплопровод­ности внутри твердого тела. В предельном случае достаточно малой теплопроводности тела можно пренебречь ею вовсе и тем­пературу каждой точки поверхности тела считать просто равной температуре жидкости в той же точке, получающейся в резуль­тате решения уравнения (55,1) с граничным условием дТ/дп=0, т. е. условием исчезновения потока тепла через поверхность тела. В обратном предельном случае достаточно большой теплопро­водности тела можно приближенно потребовать одинаковости температуры во всех точках его поверхности; производная дТ/дп при этом, вообще говоря, не обращается в нуль на всей поверх­ности и следует требовать исчезновения лишь полного потока тепла через всю поверхность тела (т. е. интеграла от дТ/дп по этой поверхности). В обоих этих предельных случаях коэффи­циент теплопроводности тела не входит явно в решение задачи; ниже мы будем предполагать, что имеем дело с одним из них.

В уравнения (55,1) и (53,3) входят постоянные параметры %, v и с_р и, кроме того, в их решение войдут размеры тела / и скорость U набегающего потока. (Разность же температур Т\ — Г_в не является теперь произвольным параметром, а должна сама быть определена в результате решения уравнений.) Из этих параметров можно составить две независимые безразмерные комбинации, в качестве которых выберем R и Р. Тогда можно утверждать, что искомая разность Т\ — Т₀ равна какой-либо ве­личине с размерностью температуры (в качестве таковой выбе­рем и²/с_р), умноженной на функцию от R и Р:

T\ —

T₀-^-f(R, P).

<-D

(55,2)

(55,3)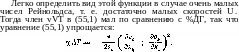

Температура и скорость испытывают заметное изменение на про­тяжении расстояний порядка размеров / тела. Поэтому оценка обеих сторон уравнения (55,3) дает

X (^ri - Т₀) vU²

I² с_рР '

Таким образом, приходим к результату, что при малых R

и²

т, — Г₀ = const -Р—, (55,4)

Ср

где const — численная постоянная, зависящая от формы тела. Отметим, что разность температур оказывается пропорциональ­ной квадрату скорости U.

Некоторые общие заключения о виде функции f (Р, R) в (55,2) можно сделать и в обратном предельном случае больших R, когда скорость и температура меняются только в узком по­граничном слое. Пусть б и б' — расстояния, на которых меняют­ся соответственно скорость и температура; б и б' отличаются друг от друга множителем, зависящим от Р. Количество тепла, выделяемое в пограничном слое в единицу времени благодаря вязкости, дается интегралом (16,3). Отнесенное к единице пло­щади поверхности тела, оно равно по порядку величины vp(C//6)²6 = vpU²/8. С другой стороны, это тепло должно быть равно теплу, теряемому телом и равному потоку

дТ Г, — т₀

Сравнив оба выражения, приходим к результату

Г,-Г₀ = -7^(Р). (55,5)

Ср

Таким образом, и в этом случае функция / оказывается не за­висящей от R; зависимость же ее от Р остается неопределенной.

Задачи

1. Определить распределение температуры в жидкости, совершающей пуазейлевское течение по трубе кругового сечения, стенки которой поддер­живаются при постоянной температуре 7V

Решение. В цилиндрических координатах с осью г по оси трубы имеем

^{*-с-2в[1-(-£-У].}

где v — средняя скорость течения. Подстановка в (55,3) приводит к уравне­нию

1jL( *1Л = _ ^{1662 v} 2 г dr У dr ) R* %cp ^T "

Решение этого уравнения, конечное при г = 0 и удовлетворяющее условию Т = То при г — R, есть

2. Определить разность температур между твердым шаром и обтекающей его жидкостью при малых числах Рейнольдса; теплопроводность шара пред­полагается большой.

Решение. Выбираем сферические координаты г, 9, ф с началом в цен­тре шара и полярной осью вдоль направления скорости и натекающего по­тока Вычисляя компоненты тензора dvi/дхц + dvk/dx_t с помощью формул (15,20) и формулы (20,9) для скорости жидкости, обтекающей шар, получаем уравнение (53,3) в виде

1 д ( _г дТ \ 1 д ( . _йдТ\ _

Т²' дг V- дг ) ⁺ г² sin 9 59 l,^{sln 0} 59 ) ~

= _A-^[cos²9(j5- —+ —)_+7Г_|,

где

л ⁹ 2 ^Р

А = — и² —. 4 с_р

Ищем Г (г, 9) в виде

Г = /(г) cos² 9+ §(/•)

и получаем после отделения частей, зависящей и не зависящей от 9, два уравнения для f и g:

г²£" + 2л£' + 2/ = -Л^-.

Из первого получаем:

' ^— { 4r² г⁴ 12 г« J г³

(член вида const л² опускаем как не исчезающий на бесконечности), после чего второе приводит к решению

_ А (3 R² \ R* 1 R^s\ dR³ c₂R ⁸~~ 2 V2 г^{2 +} 3 г* ⁺ 18 г⁸ ) Зг^{3 +} г ^+Сз>

Постоянные Ci, с₂, с₃ определяются из условий

f ОТ

Т = const и \ — г² sin 9 с(9 = 0 при г = R, что эквивалентно требованию

НЯ) = о, £'(Я) + уПЯ) = 0;

на бесконечности должно быть Т = 7V Находим:

5 2

с, = — -g-Д c₂=-g-A сз = 7^,₀.

Для разности температур шара (T{ = T(R)) и жидкости (Г₀) получаем:

т,-Т - - Р — Г,-7-₀_ ₈ Р—•

Заметим, что найденное распределение температуры оказывается удовле­творяющим и условию дТ/дг = 0 при г — R, т.е. f'(R)= g'{R) = 0. По­этому оно является одновременно и решением той же задачи в случае малой теплопроводности шара.