
- •§ 1. Уравнение непрерывности
- •§ Pvrff,
- •§ 2. Уравнение Эйлера
- •§ 3. Гидростатика
- •§ 4. Условие отсутствия конвекции
- •§ 5. Уравнение Бернулли
- •§ 6. Поток энергии
- •§ 7. Поток импульса
- •§ 8. Сохранение циркуляции скорости
- •§ 9. Потенциальное движение
- •§ 10. Несжимаемая жидкость
- •§ 12. Гравитационные волны
- •§ 13. Внутренние волны в несжимаемой жидкости
- •§ 14. Волны во вращающейся жидкости
- •Глава II
- •§ 15. Уравнения движения вязкой жидкости
- •§ 16. Диссипация энергии в несжимаемой жидкости
- •§17. Течение по трубе
- •§ 18. Движение жидкости между вращающимися цилиндрами
- •§ 19. Закон подобия
- •§ 20. Течение при малых числах Рейнольдса
- •§ 21. Ламинарный след
- •§ 22. Вязкость суспензий
- •§ 23. Точные решения уравнений движения вязкой жидкости
- •§ 24. Колебательное движение в вязкой жидкости
- •§ 25. Затухание гравитационных волн
- •Глава III
- •§ 26. Устойчивость стационарного движения жидкости
- •§ 27. Устойчивость вращательного движения жидкости
- •§ 29. Неустойчивость тангенциальных разрывов
- •§ 30. Квазипериодическое движение и синхронизация частот3)
- •§ 31. Странный аттрактор
- •§ 32. Переход к турбулентности путем удвоения периодов
- •§ 33. Развитая турбулентность
- •§ 34. Корреляционные функции скоростей
- •§ 35. Турбулентная область и явление отрыва
- •§ 36. Турбулентная струя
- •§ 37. Турбулентный след
- •§ 38. Теорема Жуковского
- •Глава IV
- •§ 39. Ламинарный пограничный слой
- •1. Определить толщину пограничного слоя вблизи критической точки (см. § 10) на обтекаемом жидкостью теле.
- •2. Определить движение в пограничном слое при конфузорном (см. § 23) течении между двумя пересекающимися плоскостями (к.. Pohlhausen, 1921).
- •§ 41. Устойчивость движения в ламинарном пограничном слое
- •2) Эта аналогия указана а в. Тимофеевым (1979) и а а Андроновым и а л. Фабрикантом (1979); ниже мы следуем изложению а. В. Тимофеева.
- •8) При V"(y) шг 0 уравнение (41,2) вообще не имеет решений, удовлетворяющих необходимым граничным условиям.
- •§ 42. Логарифмический профиль скоростей
- •§ 43. Турбулентное течение в трубах
- •§ 44. Турбулентный пограничный слой
- •§ 45. Кризис сопротивления
- •§ 46. Хорошо обтекаемые тела
- •§ 47. Индуктивное сопротивление
- •§ 48. Подъёмная сила тонкого крыла
- •S2(£)-Citt) 6-«
- •Глава V
- •§ 49. Общее уравнение переноса тепла
- •§ 50. Теплопроводность в несжимаемой жидкости
- •§ 51. Теплопроводность в неограниченной среде
- •§ 52. Теплопроводность в ограниченной среде
- •§ 53. Закон подобия для теплопередачи
- •§ 54. Теплопередача в пограничном слое
- •ВгТт « - у«р-
- •§ 55. Нагревание тела в движущейся жидкости
- •§ 56. Свободная конвекция
- •§ 57. Конвективная неустойчивость неподвижной жидкости
- •§ 58. Уравнения гидродинамики для жидкой смеси
- •§ 59. Коэффициенты диффузии и термодиффузии
- •§ 60. Диффузия взвешенных в жидкости частиц
- •Глава VII
- •§ 61. Формула Лапласа
- •§ 62. Капиллярные волны
- •§ 63. Влияние адсорбированных пленок на движение жидкости
- •Глава VIII
- •§ 64. Звуковые волны
- •§ 66. Энергия и импульс звуковых волн
- •§ 66. Отражение и преломление звуковых волн
- •§ 67. Геометрическая акустика
- •§ 68. Распространение звука в движущейся среде
- •§ 69. Собственные колебания
- •§ 70. Сферические волны
- •§71. Цилиндрические волны
- •§ 72. Общее решение волнового уравнения
- •Ctjc42-(X-q2- (*/-г,)2'
- •§ 73. Боковая волна
- •§ 74. Излучение звука
- •§ 75. Возбуждение звука турбулентностью
- •V 1г' 4я j дхидх1к
- •§ 76. Принцип взаимности
- •§ 77. Распространение звука по трубке
- •§ 78. Рассеяние звука
- •§ 79. Поглощение звука
- •4. Определить дополнительное поглощение звука, распространяющегося в смеси двух веществ, связанное с диффузией (и. Г. Шапошников и 3. А Гольдберг, 1952).
- •§ 80. Акустическое течение
- •§ 81. Вторая вязкость
- •Глава IX
- •§ 82. Распространение возмущений в потоке сжимаемого газа
- •2) Во избежание недоразумений оговорим, что если перед обтекаемым телом возникает ударная волна, то эта область несколько увеличивается (см. § 122).
- •§ 83. Стационарный поток сжимаемого газа
- •§ 84. Поверхности разрыва
- •§ 85. Ударная адиабата
- •2) Такой выбор системы координат будет подразумеваться везде в этой главе, за исключением § 92.
- •§ 86. Ударные волны слабой интенсивности
- •§ 87] Направление изменения величин в ударной волне 463
- •§ 87. Направление изменения величин в ударной волне
- •§ 88. Эволюционность ударных волн
- •§ 89. Ударные волны в политропном газе
- •1. Получить формулу
- •§ 90. Гофрировочная неустойчивость ударных волн
- •2) Сравните с аналогичной ситуацией для тангенциальных разрывов — задача 2 § 84.
- •1) Эта неустойчивость тоже была указана с. П. Дьяковым (1954); правильное значение нижней границы в (90,17) найдено в. М. Конторовичем (1957).
- •§ 91. Распространение ударной волны по трубе
- •§ 92. Косая ударная волна
- •§ 93. Ширина ударных волн
- •§ 94. Ударные волны в релаксирующей среде
- •§ 96. Слабые разрывы
- •Глава X
- •§ 97. Истечение газа через сопло
- •§ 98. Вязкое движение сжимаемого газа по трубе
- •§ 99. Одномерное автомодельное движение
- •5. Определить движение в изотермической автомодельной волне разрежения.
- •§ 100. Разрывы в начальных условиях
- •§ 101. Одномерные бегущие волны
- •§ 102. Образование разрывов в звуковой волне
- •§ 103. Характеристики
- •§ 104. Инварианты Римана
- •§ 105. Произвольное одномерное движение сжимаемого газа
- •§ 106. Задача о сильном взрыве
- •§ 107. Сходящаяся сферическая ударная волна
- •2) Эта задача была рассмотрена независимо Гудерлеем (о. Guderleu, 1942) и л. Д. Ландау и к. П. Станюковичем (1944, опубликовано в 1955).
- •§ 108. Теория «мелкой воды»
- •Глава XI
- •§ 109. Волна разрежения
- •§ 111. Пересечение ударных волн с твердой поверхностью
- •§ 112. Сверхзвуковое обтекание угла
- •§ 113. Обтекание конического острия
- •Глава XII
- •§ 114. Потенциальное движение сжимаемого газа
- •§ 115. Стационарные простые волны
- •§ 116. Уравнение Чаплыгина (общая задача
- •§ 117. Характеристики плоского стационарного течения
- •§ 118. Уравнение Эйлера — Трикоми. Переход через звуковую скорость
- •§1191 Решение уравнения эйлера —трикоми 619
- •§ 119. Решения уравнения Эйлера — Трикоми вблизи неособых точек звуковой поверхности
- •§ 120. Обтекание со звуковой скоростью
- •§ 121. Отражение слабого разрыва от звуковой линии
- •Глава XIII
- •§ 122. Образование ударных воли при сверхзвуковом обтекании тел
- •§ 123. Сверхзвуковое обтекание заостренного тела
- •§ 124. Дозвуковое обтекание тонкого крыла
- •§ 125. Сверхзвуковое обтекание крыла
- •§ 126. Околозвуковой закон подобия
- •§ 127. Гиперзвуковой закон подобия
- •Глава XIV
- •§ 128. Медленное горение
- •§ 129. Детонация
- •§ 130. Распространение детонационной волны
- •§ 131. Соотношение между различными режимами горения
- •§ 132. Конденсационные скачки
- •Глава XV
- •§ 133. Тензор энергии-импульса жидкости
- •§ 134. Релятивистские гидродинамические уравнения
- •§ 135. Ударные волны в релятивистской гидродинамике
- •§ 136. Релятивистские уравнения движения вязкой и теплопроводной среды
- •§ 137. Основные свойства сверхтекучей жидкости
- •§ 138. Термомеханический эффект
- •§ 139. Уравнения гидродинамики сверхтекучей жидкости
- •§ 140. Диссипативные процессы в сверхтекучей жидкости
- •§ 141. Распространение звука в сверхтекучей жидкости
§ 53. Закон подобия для теплопередачи
Процессы теплопередачи в жидкости осложняются по сравнению с теплопередачей в твердых телах возможностью движения жидкости. Погруженное в движущуюся жидкость нагретое тело охлаждается значительно быстрее, чем в неподвижной жидкости, где теплопередача происходит только с помощью процессов теплопроводности. О движении неравномерно нагретой жидкости говорят как о конвекции.
Будем предполагать, что имеющиеся в жидкости разности температур достаточно малы для того, чтобы ее физические свойства можно было считать не зависящими от температуры. С другой стороны, эти разности будут предполагаться настолько большими, чтобы по сравнению с ними можно было пренебречь изменениями температуры, обусловленными выделением тепла, связанным с диссипацией энергии путем внутреннего трения (см. § 55). Тогда в уравнении (50,2) может быть опущен член, содержащий вязкость, так что остается
~ + WT = %AT, (53,1)
где % — х/рСр — температуропроводность. Это уравнение вместе с уравнением Навье-Стокса и уравнением непрерывности пол-
ностью описывает конвекцию в рассматриваемых условиях. Ниже мы будем рассматривать стационарное конвективное движение1)- Тогда все производные по времени выпадают, и мы получаем следующую систему основных уравнений:
vvr = XAr, (53,2)
(vv)v=-V-^- + vAv, divv = 0. (53,3)
В эту систему, в которой неизвестными функциями являются v, Г и р/р, входят всего два постоянных параметра: v и Кроме того, решение этих уравнений зависит, через посредство граничных условий, еще от некоторого характерного параметра длины I, скорости U и характерной разности температур 7\ — Го. Первые два определяют, как всегда, размеры фигурирующих в задаче твердых тел и скорость основного потока жидкости, а третий— разность температур между жидкостью и твердыми телами.
При составлении безразмерных величин из имеющихся в нашем распоряжении параметров возникает вопрос о том, какую размерность следует приписать температуре. Для этого замечаем, что температура определяется уравнением (53,2), являющимся линейным и однородным по Г. Поэтому температура может быть умножена без нарушения уравнений на произвольный постоянный множитель. Другими словами, единицы для измерения температуры могут быть выбраны произвольным образом. Возможность такого преобразования температуры может быть учтена формально посредством приписывания ей некоторой особой размерности, которая бы не входила в размерности остальных величин. Таковой является как раз размерность градуса — единицы, в которой температура обычно и измеряется.
Таким образом, конвекция характеризуется в рассматриваемых условиях пятью параметрами со следующими размерностями:
[v] = [%] = см2/с, [С/] = см/с, М = см, [Т{ — Г0] = град.
Из них можно составить две независимые безразмерные комбинации. В качестве таковых мы выберем число Рейнольдса R =» = Ul/v и число Прандтля, определяемое как отношение
P=v/5c. (53,4)
4)
Для того чтобы конвекция могла быть
стационарной, необходимо, строго
говоря, чтобы в соприкасающихся с
жидкостью твердых телах находились
источники тепла, поддерживающие их
при постоянной температуре.
2)
Иногда пользуются числом
Пекле
(Peclet),
определяемым
как Оно сводится к произведению RP,
Что касается числа Прандтля, то оно представляет собой просто некоторую материальную константу вещества и не зависит от свойств самого потока. У газов это число — всегда порядка единицы. Значения же Р для различных жидкостей лежат в более широком интервале. У очень вязких жидкостей Р может достигать очень больших значений. Приведем в качестве примера значения Р при 20 °С для ряда веществ:
воздух . вода . . спирт . глицерин ртуть .
0,733 6,75 16,6 7250 0,044
Подобно тому как было сделано в § 19, мы можем теперь заключить, что в стационарном конвекционном потоке (заданного типа) распределение температуры и скорости имеет вид
/(f. *.р). 7j = *(-b *)• <53'5>
Безразмерная функция, определяющая распределение температуры, зависит как от параметров от обоих чисел R и Р; распределение же скоростей — только от числа R, поскольку оно определяется уравнениями (53,3), в которые теплопроводность не входит вовсе. Два конвекционных потока подобны, если их числа Рейнольдса и Прандтля одинаковы.
Теплопередачу между твердыми телами и жидкостью характеризуют обычно так называемым коэффициентом теплопередачи а, определяемым как отношение
а
= т
q
т
, (53,6)
где q — плотность потока тепла через поверхность тела, а ^ — — Т0 — характерная разность температур твердого тела и жидкости. Если распределение температуры в жидкости известно, то коэффициент теплопередачи легко определить, вычисляя плотность потока тепла q — —кдТ/дп на границе жидкости (производная берется по нормали к поверхности тела).
Коэффициент теплопередачи является размерной величиной. В качестве безразмерной величины, характеризующей теплопередачу, пользуются числом Нуссельта
N = al/%. (53,7)
Из соображений подобия следует, что для каждого данного типа конвекционного движения число Нуссельта является определенной функцией только от чисел Рейнольдса и Прандтля:
N = /(R,P). (53,8)
Эта функция приобретает тривиальный вид при конвекции с достаточно малыми числами Рейнольдса. Малым R соответствуют малые скорости движения. Поэтому в первом приближении в уравнении (53,2) можно пренебречь членом, содержащим скорость, так что распределение температуры определяется уравнением АТ" = 0, т. е. обычным уравнением стационарной теплопроводности в неподвижной среде. Коэффициент теплопередачи не может, очевидно, зависеть теперь ни от скорости, ни от вязкости жидкости и потому должно быть просто
N = const, (53,9)
причем при вычислении этой постоянной можно рассматривать жидкость как неподвижную.
Задача
Определить распределение температуры в жидкости, совершающей пуазей-левское течение по трубе кругового сечения, температура стенки которой меняется вдоль длины трубы по линейному закону.
Решение. Условия течения одинаковы во всех сечениях трубы; и распределение температуры можно искать в виде Т = Аг+ /(/•), где Аг — температура стенки (выбраны цилиндрические координаты с осью г по оси трубы). Для скорости имеем согласно (17,9)
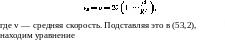 Решение
этого уравнения, не имеющее особенностей
при г
=
0
и
удовлетворяющее условию f
=
0 при г
—
R,
есть
Решение
этого уравнения, не имеющее особенностей
при г
=
0
и
удовлетворяющее условию f
=
0 при г
—
R,
есть
'«--^[4-Ш'+т(*)Т-
Плотность потока тепла
q — %
дТ дг
= -~pcpvRA.
•R *
Она не зависит от теплопроводности.
