§ 134. Релятивистские гидродинамические уравнения

Уравнения движения содержатся, как известно, в уравнениях

дТ^к

-рг = 0. (134,1)

дх

выражающих собой законы сохранения энергии и импульса той физической системы, к которой относится тензор T^ik. Воспользо­вавшись выражением (133,2) для Р^к, мы получим отсюда урав­нения движения жидкости; при этом, однако, необходимо допол­нительно учесть сохранение числа частиц, не содержащееся в уравнениях (134,1). Подчеркнем, что тензор энергии-импульса (133,2) не учитывает никаких диссипативных процессов (в том числе вязкости и теплопроводности); поэтому речь идет об урав­нениях движения идеальной жидкости.

Для формулирования уравнения, выражающего сохранение числа частиц в жидкости (уравнения непрерывности), введем 4-вектор тока частиц п¹. Его временная компонента есть плот­ность числа частиц, а пространственные компоненты составляют трехмерный вектор тока частиц. Очевидно, что 4-вектор п' дол­жен быть пропорционален 4-скорости и,¹, т. е. иметь вид

п¹ = пи⁽, (134,2)

где п — скаляр; из его определения ясно, что п — собственная плотность числа частиц³⁴). Уравнение непрерывности выражается просто равенством нулю 4-дивергенции вектора тока:

д(пи³⁵)

0. (134,3>

дх'

Возвратимся к уравнениям (134,1). Дифференцируя выраже­ние (133,2), получим

дТ^к diwu") „ du_t dp

^^_Ui.__ ₊ ^_i.___₌₌₀. (134,4)

Умножим это уравнение на и\ т. е. спроецируем его на направ­ление 4-скорости. Помня, что щи' — 1, а потому щди³⁶/дх^к = О, находим

i^>_„*^ = 0. (134,5>

дх дх

Заменив тождественно wu^k = nu^k(w/n) и воспользовавшись уравнением непрерывности (134,3), переписываем это уравнение в виде

ft Г д w 1 др 1 _п

пи г ^ = 0.

1дх^к п п дх^к J

Согласно известному термодинамическому соотношению для теп­ловой функции имеем

d^.=Td± + ±dp (134,6)

(Т— температура, о — энтропия, отнесенная к единице собствен­ного объема)³⁷). Отсюда видно, что выражение в квадратных скобках есть производная Тд(о/п) /дх^к. Опустив множитель пТ, приходим, таким образом, к уравнению

_B*_^.i_3BJ_i _{= 0}, (134,7)

дх п ds п

выражающему адиабатичность движения жидкости (d/ds озна­чает дифференцирование вдоль мировой линии движения дан­ного элемента жидкости). С помощью уравнения непрерывности (134,3) его можно представить в эквивалентном виде

— au^l = Q, (134,8)

дх

т. е. как равенство нулю 4-дивергенции потока энтропии си'.

Спроецируем теперь уравнение (134,1) на направление, нор­мальное к и¹. Другими словами, составим их комбинацию¹)

i

дТ* _k dT_k

_т — щи—_г = 0

дх^к дх¹

(выражение в левой стороне тождественно обращается в ноль при скалярном умножении на и¹). Простое вычисление приводит к уравнению

,. ди, др ъ др

™*1?=17-^в'"1?- ⁽¹³⁴'⁹⁾

Три пространственные компоненты этого уравнения представ­ляют собой релятивистское обобщение уравнения Эйлера (вре­менная же компонента есть следствие первых трех).

Уравнение (134,9) может быть представлено в другом виде в случае изэнтропического движения (подобно преобразованию от (2,3) к (2,9) для нерелятивистского уравнения Эйлера). При о/п — const имеем, согласно (134,6),

др ^ д w

дх¹ дх¹ п

и уравнение (134,9) принимает вид

« 7Т(—"*) = ТТ —• (134,10)

дх \п ) дх п

Если движение к тому же еще и стационарно (все величины не зависят от времени), то пространственные компоненты

(134,10) дают

V<vY)(^v) _{+ C}^ = 0.

Умножив это уравнение скалярно на v, после простых преоб­разований получим (vV) (yw/n) — 0. Отсюда следует, что вдоль каждой из линий тока постоянна величина

yw/n = const.

(134,11)

Это — релятивистское обобщение уравнения Бернулли¹).

Не предполагая изэнтропическое течение стационарным, легко видеть, что уравнения (134,10) имеют решения вида

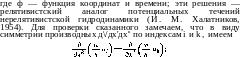умножив это равенство скалярно на и" и раскрыв производную в правой стороне, действительно вернемся к уравнению (134,10). Пространственные и временная компоненты равенства (134,12) дают:

w _r, w , d<f _A

у—v=vm, су г--зг = 0-

■ nc ^ ' n ¹ dt

Первое из них в нерелятивистском пределе дает обычное усло­вие потенциальности, а второе — уравнение (9,3) (с соответ­ствующим переобозначением <р/ст->-ф).

Рассмотрим распространение звука в среде с релятивистским уравнением состояния (т. е. в котором давление сравнимо с плот­ностью внутренней энергии, включающей в себя энергию покоя). Гидродинамические уравнения звуковых волн могут быть линеа­ризованы; при этом удобнее исходить непосредственно из записи уравнений движения в исходном виде (134,1), а не из эквива­лентных им уравнений (134,8—9). Подставив выражения (133,3) компонент тензора энергии-импульса и сохранив везде лишь величины первого порядка малости по амплитуде волны, полу­чим систему уравнений

de' dt

= — wdiv\

— — = -Vd'

c² dt ^xp '

(134,13)

где штрихом отмечены переменные части величин в волне. Исключив отсюда v, найдем:

at²

д³⁸е'

с³⁹г\р\

Наконец, написав ё = (де/др)_ллр', получим для р' волновое уравнение со скоростью звука ')

^{«=<ш:: ('«.»»}

(индекс «ад» указывает, что производная должна быть взята для адиабатического процесса, т. е. при постоянном о/п). Эта формула отличается от соответствующего нерелятивистского вы­ражения тем, что вместо обычной плотности массы здесь стоит е/с⁴⁰. Для ультра релятивистского уравнения состояния р = е/3 скорость звука и = с/л/З.

Наконец, скажем несколько слов о гидродинамических урав­нениях при наличии существенных гравитационных полей, т. е. в общей теории относительности. Они получаются из уравнений (134,8—9) просто путем замены обычных производных кова-риантными ⁴¹)

_WU^k_{Uf. * = -рг - тт- (*"'): ' = °- (134,15)}

дх дх

Выведем из этих уравнений условие механического равнове­сия в гравитационном поле. При равновесии гравитационное поле статично; можно выбрать такую систему отсчета, в которой вещество неподвижно («^а = 0, и° = £₀<Г^1/2), все величины не за­висят от времени, а смешанные компоненты метрического тен­зора равны нулю (goa = 0). Пространственные компоненты уравнения (134,15) дают тогда

_шГо_ыо_{ц =}±_?_䧙^ ЁР_

^{а0 и} 2 g₀₀ дх^а дх*'

или

w дх^а 2 дх^а

1 dp _ I

ngoo- (134,16)

') Которая в этой главе будет обозначаться посредством и.

Это и есть искомое уравнение равновесия. В нерелятивист­ском предельном случае w = рс⁴², g₀₀ — 1 + 2q>/c⁴³ (ip — ньютонов­ский гравитационный потенциал), и уравнение (134,16) перехо­дит в

Чр = — рУф, т. е. в обычное гидростатическое уравнение.

Задачи

1. Найти решение гидродинамических уравнений, описывающее одномер­ную нестационарную простую волну.

Решение. В простой волне все величины могут быть выражены в виде функции любой одной из них (см. § 101). Написав уравнения движения в виде

6Тоо дТы _ дТу дТ_и __п

cdt дх ' cdt дх

и считая 7"оо, 7\н, ^тч функциями друг от друга, получим соотношение dTdodTii = (dToi)². В него надо подставить

^roo = ^eul + Р^ии ^T0[=^wua^uu ^гп =«"i + Р"о>

2 2

учитывая при этом, чтощ — u, = 1 (при вычислении удобно ввести параметр т) согласно и₀ = ch r|, »i = — sh ti). В результате вычисления получается:

Arth — = ± — \ — de (2)

С С J W

(и — скорость звука). Далее, из (1) находим:

дх dT_m

dt dT,

00

и, вычисляя эту производную, получим:

Формулы (2), (3) и определяют искомое решение.

2. Написать гидродинамические уравнения для ультрарелятивистской сре­ды с неопределенным числом частиц (которое само определяется условиями термодинамического равновесия).

Решение. Условие термодинамического равновесия, определяющее чис ла частиц в такой среде состоит в равенстве нулю всех химических потен­циалов. Тогда е — То + р = 0, т. е. w = Та, а согласно термодинамическому выражению дифференциала тепловой функции (при заданном — единичном — объеме и нулевых химических потенциалах) dw = Tda -f dp; комбинируя обе формулы, получим: dp = adTⁱ). Уравнение (134,5) (в котором еще не ис­пользовалось уравнение непрерывности) приводит к уравнению адиабатично-сти в форме (134,8). Уравнение же (134,9) принимает вид

k дТи_{ дТ

U г-= _г.

дх^к дх¹

') При ультрарелятивистском уравнении состояния р = е/3 из написан­ных формул легко найти, что е оо Г⁴, а оо Т^а, т. е. те же законы, которые справедливы для черного излучения (см. V § 63), —как и следовало ожи­дать.