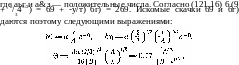§ 121. Отражение слабого разрыва от звуковой линии

Рассмотрим, снова с помощью уравнения Эйлера — Трикоми, отражение слабого разрыва от звуковой линии.

Будем считать, что падающий на звуковую линию слабый разрыв («приходящий» по отношению к точке их пересечения) — обычного типа, возникающего, скажем, при обтекании острых

углов, т. е. разрыв первых производных скорости по координа­там. Он отражается от звуковой линии в виде другого разрыва, характер которого, однако, заранее неизвестен и должен быть определен путем исследования течения в окрестности точки пе­ресечения. Последнюю выбираем ниже в качестве начала коор­динат х, у, а ось х — вдоль направления скорости газа в этой точке; тогда ей соответствует начало координат и в плоскости годографа.

Слабые разрывы расположены, как мы знаем, вдоль харак­теристик. Пусть приходящему разрыву соответствует в пло-

У /а

/

/

4

а)

- Слабый разрыв ■ Звуковая линия.

б)

h

А г I \

d 'а ' С

Рис. 125

скости годографа характеристика Оа (рис. 125,а). Непрерыв­ность координат х, у на разрыве означает, что должны быть непрерывными первые производные Ф„, Фе. Напротив, вторые производные от Ф -выражаются через первые производные от скорости по координатам и потому должны испытывать разрыв. Обозначая скачки величин квадратными скобками, имеем, таким образом: на Оа:

[<ГУ = [Фе] = 0; [Фее], [Ф_вчЬ [Ф J Ф 0. (121,1)

Сами же функции Ф в областях / и 2 по обе стороны от харак­теристики Оа не должны иметь на ней никаких особенностей. Та­кое решение можно построить с помощью второго члена в (118,6) с k —11/12, пропорционального квадрату разности (1—4г)³/90²) (второе же независимое решение Фц/12 имеет на характеристике особенность — см. ниже); первые производные этой функции на характеристике обращаются в нуль, а вто­рые — конечны. Кроме того, в Ф могут войти такие частные ре­шения уравнения Эйлера — Трикоми, которые не приводят ни к каким особенностям течения в физической плоскости. Наиболее низким по степеням Э и п таким решением является От) (§ 119). Таким образом, вблизи характеристики Оа ищем Ф в виде

Ф_а1 = -Л_ч9-^'^(-|,

o_a2 = -^e-ceⁿ'⁶6²F(|-, -Ц.

3; |). 3; б).

(121,2)

где индексы а\ и а2 указывают окрестности по обе стороны ха­рактеристики (в областях / и 2); А, В, С — постоянные, и снова введено обозначение

t ₌ l _i!!L

(на характеристике | = 0).

Мы увидим ниже, что в зависимости от знака произведения АВ могут иметь место два случая: слабый разрыв отражается в виде слабого же разрыва другого (логарифмического) харак­тера или в виде ударной волны малой интенсивности.

Отражение в виде слабого разрыва

Рассмотрим сначала первый из этих случаев (Л. Д. Ландау, Е. М. Лифшиц, 1954). Отраженному от звуковой линии слабому разрыву соответствует в плоскости годографа вторая характе­ристика (Ob на рис. 125,а). Вид функции Ф вблизи этой харак­теристики устанавливается путем аналитического продолжения функций (121,2) согласно формулам (118,11—13). Однако при 11/12 функция F\ теряет смысл и поэтому непосредственно воспользоваться этими формулами нельзя. Вместо этого надо положить в них сначала &= 11/12+ е, после чего устремить в к нулю. В соответствии с общей теорией гипергеометрического уравнения при этом появляются логарифмические члены.

В результате вычисления (с помощью (118,13)) для функции Ф вблизи характеристики Ob в области 3 получается следующее выражение (с точностью до членов второго порядка по \ вклю­чительно) :

Ф_Ьз = - Л0г, + £(- 0)^и/б a² InШ + с₀ + с,Е + с₂|²}, (121,3)

* где Со, Си С2 — числовые постоянные¹). Аналогичное преобразо­вание (с помощью (118,11)) функции Фаг от окрестности харак­теристики Оа к окрестности характеристики Ob дает функцию Ф_Ь2, отличающуюся от (121,3) лишь заменой В на С/2. Коорди­наты х, у точек характеристики в физической плоскости вычис-

) Значение этих постоянных:

с„ = -2⁹ • 3⁴/385 = - 108, с, = 288/7 = 41,1, с₂ = 4,86.

ляются как производные (118,4), взятые при £ = 0. Так, исходя из (121,3) найдем

*₌_ле--!^(-еГ,

* (121,4)

. ( 39 \^2/3 В ( 11 , с, \, ыЫб

а дифференцирование функции Фь₂ даст такие же выражения с С/2 вместо В. Условие непрерывности координат х, у на ха­рактеристике Ob приводит, следовательно, к соотношению

С = 2В. (121,5)

Далее, для осуществления рассматриваемой картины отраже­ния должны отсутствовать предельные линии в плоскости годо­графа (и тем самым — нефизические области в этой плоскости), т. е. якобиан Д нигде не должен проходить через нуль. Вблизи характеристики Оа якобиан вычисляется с помощью функций

2. и оказывается положительным (главный член в нем: Д «Л²). Вблизи же характеристики Ob вычисление с помощью

3. дает

Д ~ А² - 16 (|)"⁶ ЛЯГ,"⁴ In |||. (121,6)

При приближении к характеристике логарифм стремится к —с», и главным является второй член. Поэтому из условия Д > 0 имеем А В > 0, т. е. А и В должны иметь одинаковый знак.

Наконец, для определения формы звуковой линии нам пона­добятся выражения для Ф вблизи оси ц = 0. Выражение, при­годное в окрестности верхней части этой оси, получается просто преобразованием гипергеометрической функции в Ф (121,2) в гипергеометрические функции аргумента 1 —- g = 4r)^s/98², обра­щающегося в нуль при п^О¹). Сохранив лишь члены наиболее низких степеней по г\, получим

^Ф_а ^{= -Атф-} _r(23/^2f₂₎^(ffi_17/12) ^{Д9"/6=-Лг|8-б',25В8"/6- (121,7)}

Аналитическое же продолжение в область нижней части оси дает

Ф_с=- Лг,8 — 6,25- УзВ8^11/6 (121,8)

(вычисления аналогичны выводу формулы преобразования (118,13)).

Теперь можно определить форму всех интересующих нас ли­ний. На характеристиках имеем, отбрасывая члены более высо-

*) Это преобразование приведено, например, в § е Математического при­ложения в III — формула (е, 7).

кого порядка: # =—Л0, у = —Лт]. Мы условились считать, что приходящему слабому разрыву отвечает верхняя характеристика (6 >0). Поскольку скорость газа направлена в положительном направлении оси х, то этот разрыв, для того чтобы быть прихо­дящим, должен лежать в полуплоскости х <с 0. Отсюда следует, что постоянная Л, а с нею и В должны быть положительными. Уравнение линии слабого разрыва в физической плоскости будет

_у = (|)^2/3Л^1/3(-х)^2/3=1,31Л^1/3(-_Л)^2/3. (121,9)

Отраженный же разрыв, соответствующий нижней характери­стике, дается уравнением')

-#=1,31Л^1/Зл:^2/3 (121,10)

(см. рис. 125,6; обозначение линий и областей на этом рисунке Соответствует обозначениям на рис. 125, а).

Уравнение звуковой линии получается из функций (121,7—8). Дифференцируя по ц и 0 и положив затем г\ = 0, получим из (121,7) уравнение той части линии, на которой 0 > 0:

х = -Л0, у = — Л.. 6,25В0^г,/6,

откуда

y=-UABA-^5l6(- xf\ (121,11)

Это — нижняя часть звуковой линии на рис. 125,6. Аналогич­ным образом из (121,8) находим уравнение верхней части этой линии:

0 = 11,4УЗ ВА-^ътх^ъ'\ (121,12)

Таким образом, оба слабых разрыва и обе ветви звуковой ли­нии имеют в точке пересечения О общую касательную (ось у), причем две ветви звуковой линии лежат по разные стороны оси у.

На приходящем разрыве испытывают скачок производные от скорости по координатам. В качестве характерной величины рас­смотрим скачок'производной (дг\/дх)_у. Имея в виду, что

( дх\ \ _ д(т|, у) ^ <?(т|, у) ,д(х, у) 1 <?^гФ

\дх )_у д (х, у) д (г), в) / д (т), 6) Д 39²

и воспользовавшись формулами (121,2), (121,5), получим для искомого скачка:

При приближении к точке пересечения он растет как (—#)^-1/4.

') С учетом первых поправочных членов (вторые члены в формулах (121,4)) уравнение отраженного разрыва:

- у = 1.31А¹ V³ - Ю,58Л -^5/V⁵. (121, 10а)

На отраженном же слабом разрыве производные скорости вообще не испытывают скачка, но распределение скоростей имеет своеобразную логарифмическую особенность. Вычислив из функ­ции (121,3) (сохранив в ней лишь первый член в скобках) ко­ординаты х и у в функции от tj, 0, можно представить зависи­мость ц от х при заданном у вблизи отраженного разрыва в следующем параметрическом виде:

т/. (121,14)

_ц = Ш- + -Л^-^1у^ А 1 -у А \у\ 6Л

где £ играет роль параметра, а Хо = хо(у)— уравнение линии разрыва в физической плоскости.

Отражение в виде ударной волны

Перейдем к рассмотрению другого случая — отражения сла­бого разрыва от звуковой линии в виде ударной волны (Л. П. Горькое, Л. П. Питаевский, 1962)').

^{e + f n3/2}

е=^т~т- 021,15)

Этот случай возникает, если произведение АВ < 0. Из (121,6) видно, что в этом случае имеется две предельные линии, экспо­ненциально близкие к характеристике Ob: якобиан А обращается в нуль при

Ля (2/3)^1/6 16|В|ч

¹⁶¹ Ю1

Заранее очевидно, что экспоненциально близкими к характери­стике будут и границы нефизической области на плоскости годо­графа (Obi и ОЬг на рис. 126,а), и тем самым будет экспонен­циально мала интенсивность ударной волны.

Пренебрегая экспоненциально малыми значениями £ на ли­ниях ОЬ₂ и ОЬ₃, мы получим для координат х, у на них те же выражения, которые мы имели на двух сторонах характеристики Ob в предыдущем случае. Поэтому условие непрерывности коор­динат на ударной волне во всяком случае приводит к прежнему соотношению (121,5). Соответственно, остается прежним и выра­жение (121,13) для скачка производной от скорости на падаю­щем разрыве. Снова приняв, что этому разрыву отвечает верхняя характеристика Оа на плоскости годографа, будем по-прежнему иметь А > 0, так что теперь В < 0. Из (121,13) видно, следо­вательно, что физическим критерием происхождения двух слу-

') Принципиальная возможность такого отражения отмечалась ранее Г у* дерлеем (К. G. Guderley, 1948).

чаев отражения слабого разрыва является знак скачка произ­водной скорости на падающем разрыве.

Остаются прежними (при пренебрежении экспоненциально малыми поправками) уравнения (121,9—10) линий падающего (слабого) и отраженного (ударной волны) разрывов. Но ввиду другого знака постоянной В меняется расположение этих линий на физической плоскости — как это показано на рис. 126,6.

а)

б)

В

Рис. 126

Для определения интенсивности ударной волны (т. е. скач­ков величин 68 и 8ц на ней) надо обратиться к полной системе граничных условий, которым должно удовлетворять на ударной волне решение уравнения Эйлера — Трикоми. Они были сформу­лированы уже в § 120: условия (120,9—11). Из них последнее, уравнение ударной поляры, принимает вид (68)² = т](6г|)², где 69 = 062 — 0»з, 6rj = Г|62 — Цьз — экспоненциально малые скачки величин на ударной волне (индексы 62 и &3 относятся к линиям ОЬг и 06₃ на плоскости годографа, т. е. соответственно к перед­ней и задней сторонам ударной волны на физической плоскости). Отсюда

60 = Ул6г,; (121,16)

выбор знака при извлечении корня определяется тем, что одно­временно с уменьшением скорости газа при его прохождении через ударную волну должно происходить приближение линий тока к поверхности разрыва.

В соответствии с (121,15) ищем уравнения линий 06₂ и ОЬз в плоскости годографа в виде

6 + 1 ту³/² = a_b2101 е-», 0 + 4 г,^,/2 = - %> 19 |в-в

(121,17)

где а — (аь2 + а_Ьъ)/2; переменные п, 9 выражены через коорди­наты на физической плоскости согласно х « —Л9, у » —Ац. Определение коэффициента а требует учета также и всех осталь­ных граничных условий, причем в них должны учитываться чле­ны как линейные, так и квадратичные по экспоненциально ма­лой величине ехр(—в). Не приводя этих довольно громоздких вычислений, укажем лишь их результат: а&₂ = «бз — а = 5,2,