
- •§ 1. Уравнение непрерывности
- •§ Pvrff,
- •§ 2. Уравнение Эйлера
- •§ 3. Гидростатика
- •§ 4. Условие отсутствия конвекции
- •§ 5. Уравнение Бернулли
- •§ 6. Поток энергии
- •§ 7. Поток импульса
- •§ 8. Сохранение циркуляции скорости
- •§ 9. Потенциальное движение
- •§ 10. Несжимаемая жидкость
- •§ 12. Гравитационные волны
- •§ 13. Внутренние волны в несжимаемой жидкости
- •§ 14. Волны во вращающейся жидкости
- •Глава II
- •§ 15. Уравнения движения вязкой жидкости
- •§ 16. Диссипация энергии в несжимаемой жидкости
- •§17. Течение по трубе
- •§ 18. Движение жидкости между вращающимися цилиндрами
- •§ 19. Закон подобия
- •§ 20. Течение при малых числах Рейнольдса
- •§ 21. Ламинарный след
- •§ 22. Вязкость суспензий
- •§ 23. Точные решения уравнений движения вязкой жидкости
- •§ 24. Колебательное движение в вязкой жидкости
- •§ 25. Затухание гравитационных волн
- •Глава III
- •§ 26. Устойчивость стационарного движения жидкости
- •§ 27. Устойчивость вращательного движения жидкости
- •§ 29. Неустойчивость тангенциальных разрывов
- •§ 30. Квазипериодическое движение и синхронизация частот3)
- •§ 31. Странный аттрактор
- •§ 32. Переход к турбулентности путем удвоения периодов
- •§ 33. Развитая турбулентность
- •§ 34. Корреляционные функции скоростей
- •§ 35. Турбулентная область и явление отрыва
- •§ 36. Турбулентная струя
- •§ 37. Турбулентный след
- •§ 38. Теорема Жуковского
- •Глава IV
- •§ 39. Ламинарный пограничный слой
- •1. Определить толщину пограничного слоя вблизи критической точки (см. § 10) на обтекаемом жидкостью теле.
- •2. Определить движение в пограничном слое при конфузорном (см. § 23) течении между двумя пересекающимися плоскостями (к.. Pohlhausen, 1921).
- •§ 41. Устойчивость движения в ламинарном пограничном слое
- •2) Эта аналогия указана а в. Тимофеевым (1979) и а а Андроновым и а л. Фабрикантом (1979); ниже мы следуем изложению а. В. Тимофеева.
- •8) При V"(y) шг 0 уравнение (41,2) вообще не имеет решений, удовлетворяющих необходимым граничным условиям.
- •§ 42. Логарифмический профиль скоростей
- •§ 43. Турбулентное течение в трубах
- •§ 44. Турбулентный пограничный слой
- •§ 45. Кризис сопротивления
- •§ 46. Хорошо обтекаемые тела
- •§ 47. Индуктивное сопротивление
- •§ 48. Подъёмная сила тонкого крыла
- •S2(£)-Citt) 6-«
- •Глава V
- •§ 49. Общее уравнение переноса тепла
- •§ 50. Теплопроводность в несжимаемой жидкости
- •§ 51. Теплопроводность в неограниченной среде
- •§ 52. Теплопроводность в ограниченной среде
- •§ 53. Закон подобия для теплопередачи
- •§ 54. Теплопередача в пограничном слое
- •ВгТт « - у«р-
- •§ 55. Нагревание тела в движущейся жидкости
- •§ 56. Свободная конвекция
- •§ 57. Конвективная неустойчивость неподвижной жидкости
- •§ 58. Уравнения гидродинамики для жидкой смеси
- •§ 59. Коэффициенты диффузии и термодиффузии
- •§ 60. Диффузия взвешенных в жидкости частиц
- •Глава VII
- •§ 61. Формула Лапласа
- •§ 62. Капиллярные волны
- •§ 63. Влияние адсорбированных пленок на движение жидкости
- •Глава VIII
- •§ 64. Звуковые волны
- •§ 66. Энергия и импульс звуковых волн
- •§ 66. Отражение и преломление звуковых волн
- •§ 67. Геометрическая акустика
- •§ 68. Распространение звука в движущейся среде
- •§ 69. Собственные колебания
- •§ 70. Сферические волны
- •§71. Цилиндрические волны
- •§ 72. Общее решение волнового уравнения
- •Ctjc42-(X-q2- (*/-г,)2'
- •§ 73. Боковая волна
- •§ 74. Излучение звука
- •§ 75. Возбуждение звука турбулентностью
- •V 1г' 4я j дхидх1к
- •§ 76. Принцип взаимности
- •§ 77. Распространение звука по трубке
- •§ 78. Рассеяние звука
- •§ 79. Поглощение звука
- •4. Определить дополнительное поглощение звука, распространяющегося в смеси двух веществ, связанное с диффузией (и. Г. Шапошников и 3. А Гольдберг, 1952).
- •§ 80. Акустическое течение
- •§ 81. Вторая вязкость
- •Глава IX
- •§ 82. Распространение возмущений в потоке сжимаемого газа
- •2) Во избежание недоразумений оговорим, что если перед обтекаемым телом возникает ударная волна, то эта область несколько увеличивается (см. § 122).
- •§ 83. Стационарный поток сжимаемого газа
- •§ 84. Поверхности разрыва
- •§ 85. Ударная адиабата
- •2) Такой выбор системы координат будет подразумеваться везде в этой главе, за исключением § 92.
- •§ 86. Ударные волны слабой интенсивности
- •§ 87] Направление изменения величин в ударной волне 463
- •§ 87. Направление изменения величин в ударной волне
- •§ 88. Эволюционность ударных волн
- •§ 89. Ударные волны в политропном газе
- •1. Получить формулу
- •§ 90. Гофрировочная неустойчивость ударных волн
- •2) Сравните с аналогичной ситуацией для тангенциальных разрывов — задача 2 § 84.
- •1) Эта неустойчивость тоже была указана с. П. Дьяковым (1954); правильное значение нижней границы в (90,17) найдено в. М. Конторовичем (1957).
- •§ 91. Распространение ударной волны по трубе
- •§ 92. Косая ударная волна
- •§ 93. Ширина ударных волн
- •§ 94. Ударные волны в релаксирующей среде
- •§ 96. Слабые разрывы
- •Глава X
- •§ 97. Истечение газа через сопло
- •§ 98. Вязкое движение сжимаемого газа по трубе
- •§ 99. Одномерное автомодельное движение
- •5. Определить движение в изотермической автомодельной волне разрежения.
- •§ 100. Разрывы в начальных условиях
- •§ 101. Одномерные бегущие волны
- •§ 102. Образование разрывов в звуковой волне
- •§ 103. Характеристики
- •§ 104. Инварианты Римана
- •§ 105. Произвольное одномерное движение сжимаемого газа
- •§ 106. Задача о сильном взрыве
- •§ 107. Сходящаяся сферическая ударная волна
- •2) Эта задача была рассмотрена независимо Гудерлеем (о. Guderleu, 1942) и л. Д. Ландау и к. П. Станюковичем (1944, опубликовано в 1955).
- •§ 108. Теория «мелкой воды»
- •Глава XI
- •§ 109. Волна разрежения
- •§ 111. Пересечение ударных волн с твердой поверхностью
- •§ 112. Сверхзвуковое обтекание угла
- •§ 113. Обтекание конического острия
- •Глава XII
- •§ 114. Потенциальное движение сжимаемого газа
- •§ 115. Стационарные простые волны
- •§ 116. Уравнение Чаплыгина (общая задача
- •§ 117. Характеристики плоского стационарного течения
- •§ 118. Уравнение Эйлера — Трикоми. Переход через звуковую скорость
- •§1191 Решение уравнения эйлера —трикоми 619
- •§ 119. Решения уравнения Эйлера — Трикоми вблизи неособых точек звуковой поверхности
- •§ 120. Обтекание со звуковой скоростью
- •§ 121. Отражение слабого разрыва от звуковой линии
- •Глава XIII
- •§ 122. Образование ударных воли при сверхзвуковом обтекании тел
- •§ 123. Сверхзвуковое обтекание заостренного тела
- •§ 124. Дозвуковое обтекание тонкого крыла
- •§ 125. Сверхзвуковое обтекание крыла
- •§ 126. Околозвуковой закон подобия
- •§ 127. Гиперзвуковой закон подобия
- •Глава XIV
- •§ 128. Медленное горение
- •§ 129. Детонация
- •§ 130. Распространение детонационной волны
- •§ 131. Соотношение между различными режимами горения
- •§ 132. Конденсационные скачки
- •Глава XV
- •§ 133. Тензор энергии-импульса жидкости
- •§ 134. Релятивистские гидродинамические уравнения
- •§ 135. Ударные волны в релятивистской гидродинамике
- •§ 136. Релятивистские уравнения движения вязкой и теплопроводной среды
- •§ 137. Основные свойства сверхтекучей жидкости
- •§ 138. Термомеханический эффект
- •§ 139. Уравнения гидродинамики сверхтекучей жидкости
- •§ 140. Диссипативные процессы в сверхтекучей жидкости
- •§ 141. Распространение звука в сверхтекучей жидкости
Глава XI
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ РАЗРЫВА
§ 109. Волна разрежения
Линия пересечения двух ударных волн является в математическом отношении особой линией двух функций, описывающих движение газа. Такой же особой линией является край всякого острого угла на поверхности обтекаемых газом тел. Оказывается возможным исследовать движение газа вблизи особой линии в самом общем виде (L. Prandtl, Th. Meyer, 1908).
Рассматривая область вблизи небольшого участка особой линии, мы можем считать последнюю прямой, которую мы выберем в качестве оси z цилиндрической системы координат г, ф, г. Вблизи особой линии все величины существенным образом зависят от угла ф. Напротив, от координаты г они зависят лишь слабо, и при достаточно малых г зависимостью от г можно вообще пренебречь. Несущественна также зависимость величин от координаты г, — изменением картины течения вдоль небольшого участка особой линии можно пренебречь.
Таким образом, мы должны исследовать стационарное движение, при котором все величины являются функциями только от
ds
ф. Уравнение сохранения энтропии vVs = 0 дает иф — = 0, откуда s = const1), т. е. движение изэнтропично. Поэтому в уравнении Эйлера можно писать Vw вместо Vp/p: (vV)jf = —Vw. В цилиндрических координатах получаем три уравнения:
г d<f г ~~ ' г dtp ~r г г d(f ' ф д<?
Из последнего имеем vz — const; без ограничения общности можно положить Vz — 0 и рассматривать движение как' плоское, — это сводится просто к соответствующему выбору скорости движения системы координат вдоль оси z. Первые два уравнения переписываем в виде
/ dvm \ 1 dp dw "о Ы" + Ч = - у ^ = - • (109,2)
') Если положить Уф = 0 (вместо ds/d(p = 0), то, как легко заключить из написанных ниже уравнений движения, получится v, = 0, vz Ф 0. Такое движение соответствовало бы пересечению поверхностей тангенциальных разрывов (со скачком скорости vz) и ввиду неустойчивости таких разрывов не представляет интереса.
Подставляя (109,1) в (109,2), получаем:
dv9 dvr dw
V* dy + Vr dq> ~ dq> "
или, интегрируя:
2,2
w
+
"ф
°r
=
const. (109.3)
Заметим, что равенство (109,1) означает, что rotv = 0, т. е. движение потенциально; в связи с этим и имеет место уравнение Бернулли (109,3).
Далее, уравнение непрерывности div(pv) = 0 дает
Р°' + т£ - р & + ^) + о, % = 0. (109,4) Используя (109,2), получим отсюда:
Но производная dp/dp, которую правильнее писать в виде (др/др) s, есть квадрат скорости звука. Таким образом,
Этому уравнению можно удовлетворить двумя способами. Во-первых, может быть
dom
-dV + vr-o.
 Тогда
из (109,2) имеем р = const,
р
= const,
а
из (109,3) получаем, что и v2
=
v2.-\-
Vy
= const,
т.
е. скорость постоянна по абсолютной
величине. Легко видеть, что и направление
скорости в этом случае постоянно. Угол
х,
образуемый
скоростью с некоторым заданным
направлением в плоскости движения,
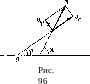
равен (рис. 96)
Тогда
из (109,2) имеем р = const,
р
= const,
а
из (109,3) получаем, что и v2
=
v2.-\-
Vy
= const,
т.
е. скорость постоянна по абсолютной
величине. Легко видеть, что и направление
скорости в этом случае постоянно. Угол
х,
образуемый
скоростью с некоторым заданным
направлением в плоскости движения,
равен (рис. 96)
X = qp + arctg-^. (109,6)
"Г
Дифференцируя это выражение по ф и используя (109,1—2), получаем после простого преобразования:
При р = const имеем, действительно, % = const. Таким образом, приравнивая нулю первый множитель в (109,5), мы получаем просто тривиальное решение — однородный поток.
Во-вторых, уравнению (109,5) можно удовлетворить, положив 1 = v2Jc2, т. е. уФ = ±с. Радиальная же скорость определится из (109,3). Обозначая в этом уравнении const посредством доо,
получаем:
Оф=±с, vr = i ^/2 (wq — w) с2 •
В этом решении перпендикулярная к радиус-вектору составляющая vv скорости в каждой точке равна по величине местной скорости звука. Полная же скорость v = д/у2 + а2, следовательно, больше скорости звука. Как абсолютная величина скорости, так и ее направление меняются от точки к точке. Поскольку скорость звука не может пройти через нуль, то ясно, что непрерывная функция иф(ср) должна быть равна везде -f-c или же везде —с. Выбирая соответствующим образом направление отсчета угла ф, мы можем условиться считать, что у,р == с. Что касается выбора знака у vr, то мы увидим ниже, что он диктуется физическими соображениями и должен быть положительным. Таким
образом:
уф = с, vr = V2 {w0 — w) — с2. (109,8)
Из уравнения непрерывности (109,4) имеем dq> =—d{pv^)/pvr. Подставив сюда (109,8) и интегрируя, получим:
(109,9)
J р л/2 (w0 — w) — с2
Если известно уравнение состояния газа и уравнение адиабаты (напомним, что s = const), то с помощью этой формулы можно определить зависимость всех величин от угла ф. Таким образом, формулы (109,8—9) полностью определяют движение газа.
Займемся теперь более подробным изучением полученного решения. Прежде всего заметим, что прямые ф = const пересекают в каждой точке линии тока под углом Маха (его синус равен Уф/у = cfv), т. е. являются характеристиками. Таким образом, одно из двух семейств характеристик (в плоскости х, у) представляет собой пучок выходящих из особой точки прямых и обладает в данном случае важным свойством — вдоль каждой из них все величины остаются постоянными. В этом смысле рассматриваемое решение играет в теории плоского стационарного движения такую же роль, какую играет изученное в § 99 автомодельное движение в теории нестационарных одномерных течений. Мы вернемся еще к этому вопросу в § 115.
Из (109,9) видно, что (рс)'<0 (' обозначает дифференциро-. вание по ф). Написав и замечая, что производная d(pc)/dp положительна (см. (99,9)), мы находим, что производная р' < 0; вместе с нею отрицательны и производные р' — с2р', до' — р'/р. Далее, из того, что производная до' отрицательна, следует, что абсолютная величина скорости 0 = у2(и>о — w)— возрастающая функция ср. Наконец, из (109,7) следует, что /' > 0. Таким образом, получаем следующие неравенства:
i£.<0, -^<0, -т->0, $L>0. (109,10) d<f dip ' dcp ^ dtp v
Другими словами, в направлении обхода вокруг особой точки, совпадающем с направлением обтекания, плотность и давление падают, а вектор скорости возрастает по абсолютной величине и поворачивается в направлении обхода.
Описанное движение часто называют волной разрежения; ниже мы будем пользоваться этим термином.
Легко видеть, что волна разрежения не может иметь места во всей области вокруг особой линии. Действительно, поскольку v есть монотонно возрастающая функция ср, то при полном обходе вокруг начала координат (т. е. при изменении ср на 2я) мы получили бы для v значение, отличное от исходного, что нелепо. Ввиду этого истинная картина движения вокруг особой линии должна представлять собой совокупность секториальных областей, разделённых плоскостями ср = const, являющимися поверхностями разрывов. В каждой из таких областей происходит либо движение, описываемое волной разрежения, либо движение с постоянной скоростью. Число и характер этих областей для различных конкретных случаев будут установлены в следующих параграфах. Сейчас укажем лишь, что граница между волной разрежения и областью однородного течения должна быть непременно слабым разрывом. Действительно, эта граница не может быть тангенциальным разрывом (разрывом скорости vr), так как на ней не обращается в нуль нормальная к ней компонента скорости уф = с. Она не может также быть ударной волной, так как нормальная компонента скорости (vv) по одну сторону от такого разрыва должна была бы быть больше, а по другую — меньше скорости звука, между тем как в данном случае с одной из сто? рон границы мы во всяком случае имеем уф = с.
Из сказанного можно вывести важное следствие. Возмущения, вызывающие образование слабых разрывов, исходят от особой линии (оси г) и распространяются по направлению от нее. Это значит, что ограничивающие волну разрежения слабые разрывы должны быть «исходящими» по отношению к этой линии, т. е. компонента скорости vr касательная к слабому разрыву должна бьггь положительна. Таким образом, мы оправдали сделанный в (109,8) выбор знака у vr.
Применим теперь полученные формулы к политропному газу. В таком газе w = c2/(y—1); уравнение же адиабаты Пуассона можно написать в виде
pc-»»v-'» = const, рс~2У«У-" = const (109,11)
(ср. (99,13)). Пользуясь этими формулами, представим интеграл (109,9) в виде
Vy+l С dc
где с» — критическая скорость (см. (83,14)). Отсюда
Ф = д/-у~т arccos -j- + const, или, выбирая начало отсчета <р так, чтобы было const = 0:
iV = c = c,cos д/-£=±ф. (109,12)
Согласно формуле (109,8) получаем отсюда:
»r=Vf^c-Sin Vttt45- <109>13>
Далее, воспользовавшись уравнением адиабаты Пуассона в виде (109,11), находим зависимость давления от угла ф:
_2V_
p=^.(cos д/ттгф)¥-' • (109,14)
Наконец, для угла х (109,6) имеем:
X = ? + arctg(^/-^}ctg д/Х^1ф) {109,15)
(угол х отсчитывается от того же направления, от которого от-считывается ф).
Поскольку должно быть vr > 0, с > 0, то угол ф в этих формулах может меняться только в пределах между ф = 0 и
ф = фтах, ГДе
qw = f VlF=T\ (109,16)
Это значит, что волна разрежения может занимать сектор с углом раствора, не превышающим фтах; так, для двухатомного газа (воздух) этот угол равен 219,3°. При изменении ф от 0 до фтах угол % меняется от я/2 до фтах. Таким образом, направление скорости в волне разрежения может повернуться нэ угол, не превышающий фтах — я/2 (для воздуха 129,3°).


Y+ 1
у — 1 * umax>
иф = с = 0,
т. е. скорость направлена по радиусу и достигает своего предельного значения итах (см. § 83).
На рис. 97 даны графики величин р/р», c*/v и % как функции угла ф для воздуха (у = 1,4).
Полезно заметить форму, ко- Рис. 98
торую имеет определяемая формулами (109,12—13) кривая в плоскости vx, vy (так называемый годограф скоростей). Это — дуга эпициклоиды, построенной между ОКРУЖНОСТЯМИ раДИуСОВ V = С* И V = Umax (РИС. 98) .
Задачи
1. Определить форму линий тока в волне разрежения. Решение. Уравнение линий тока для двухмерного движения в полярных координатах есть dr/vr — rd<p/v . Подставляя сюда (109,12—13)
:'о
(c°s
д/^+уф)
V+I Y-1
Эти линии тока представляют собой семейство подобных кривых, обращенных своей вогнутостью в сторону начала координат, являющегося центром подобия.
2. Определить наибольший возможный угол между слабыми разрывами, ограничивающими волну разрежения, при заданных значениях Vi, ct скорости газа и скорости звука на первом из них.
Решение. Для соответствующего первому разрыву значения угла ф находим из (109,12):
*-у*
+
1 с,
arccos^
Значения же фг ■= фти, так что искомый угол равен
Л/:
' V + 1 с
Фг — Ф1 = Д/ г. f arcsln -J'
Критическая скорость с« выражается через Vi, Cj уравнением Бернулли л. °> С» ■ °? V + 1 2
Наибольший возможный угол поворота скорости газа в волне разрежения получится соответственно с помощью (109,15) как разность Хш.х =■ = X(«Pi) — X(<Pj):
VY + 1 . .с, -- arcstn —• arcsm —i-. Y — 1 c, vi
Как функция от fi/Ci, Xmax имеет наибольшее значение при t>i/ct = 1
Xmax- 2 V V Y — 1 )' При t/i/ci->-oo Xmax стремится к нулю, как
_ 2 с, Xmax у — 1 о, '
§ НО. Типы пересечений поверхностей разрыва
Ударные волны могут пересекаться друг с другом; это пересечение происходит вдоль некоторой линии. Рассматривая движение в окрестности небольших участков этой линии, мы можем считать ее прямой, а поверхности разрывов — плоскими. Таким образом, достаточно рассмотреть пересечение плоских ударных волн.
Линия пересечения разрывов представляет собой в математическом отношении особую линию (как уже указывалось в начале § 109). Вся картина движения вокруг нее складывается из ряда секториальных областей, в каждой из которых имеется либо однородный поток, либо описанная в § 109 волна разрежения. Ниже излагается общая классификация возможных ти нов пересечения поверхностей разрывов ').
Прежде всего необходимо сделать следующее замечание. Если по обе стороны ударной волны движение газа является сверхзвуковым, то (как было указано в начале § 92) можно говорить о «направлении» ударной волны и соответственно этому различать ударные волны, «исходящие» от линии пересечения, и волны, «приходящие» к ней. В первом случае касательная составляющая скорости направлена от линии пересечения, и можно сказать, что возмущения, вызывающие образование разрыва, исходят от этой линии. Во втором же случае возмущения исходят из какого-то места, постороннего по отношению к линии пересечения.
Если по одну из сторон от ударной волны движение является дозвуковым, то возмущения распространякЗтея в обе стороны вдоль ее поверхности и понятие о направлении волны т"ёряет, строго говоря, смысл. Для нижеследующих рассуждений существенно, однако, что вдоль такого разрыва могут распространяться исходящие от места пересечения возмущения. В этом смысле подобные ударные волны в излагаемых ниже рассуждениях играют ту же.роль, что и чисто сверхзвуковые исходящие волны, и под исходящими ударными волнами ниже подразумеваются обе эти категории волн.
На следующих ниже рисунках изображаются картины течения в плоскости, перпендикулярной к линии пересечения. Без ограничения общности можно считать, что движение происходит в этой плоскости. Параллельная линии пересечения (а потому и всем плоскостям разрывов) компонента скорости должна быть одинакова во всех областях вокруг линии пересечения и поэтому надлежащим выбором системы координат может быть всегда обращена в нуль.
Укажем, прежде всего, некоторые заведомо невозможные конфигурации.
')
Она была дана Л.
Д.
Ландау
(1944),
а в некоторых пунктах (относящихся
к взаимодействию ударных волн с
тангенциальными и слабыми разрывами)
дополнена С.
П.
Дьякдзым
(1954).
2)
Чтобы не загромождать текст однообразными
рассуждениями, мы ге будем приводить
аналогичные соображения для случаев,
когда имеются области дозвукового
движения и уходящей волной является
в действительности ударная волна,
граничащая с дозвуковой областью.

 Далее,
поскольку пересечение не может оказывать
обратного влияния на приходящие ударные
волны, то одновременное пересечение
(вдоль общей линии) более чем двух таких
волн, возникающих от каких-то
посторонних причин, было бы невероятной
случайностью. Таким образом, в картине
пересечения могут участвовать всего
лишь одна или две приходящие ударные
волны.
Далее,
поскольку пересечение не может оказывать
обратного влияния на приходящие ударные
волны, то одновременное пересечение
(вдоль общей линии) более чем двух таких
волн, возникающих от каких-то
посторонних причин, было бы невероятной
случайностью. Таким образом, в картине
пересечения могут участвовать всего
лишь одна или две приходящие ударные
волны.
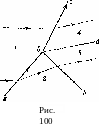
Весьма существенно следующее обстоятельство: протекающий мимо точки пересечения газ может пройти лишь через одну исходящую из этой точки ударную волну или волну разрежения. Пусть, например, газ проходит через следующие друг за другом две исходящие из точки О ударные волны, как это показано на рис. 99, в. Поскольку позади волны Оа нормальная компонента скорости v2n < с2< то тем более была бы меньше с2 нормальная к волне Ob компонента скорости в области 2 в противоречии с основным свойством ударных волн. Аналогичным образом убеждаемся в невозможности прохождения газа через следующие одна за другой исходящие из точки О две волны разрежения или волну разрежения и ударную волну.
Эти соображения, очевидно, не распространяются на приходящие к точке пересечения ударные волны.
Теперь мы можем приступить к перечислению возможных типов пересечений.
На рис. 100 изображено пересечение, в котором участвует всего одна приходящая ударная волна Оа; две другие ударные волны Ob и Ос являются исходящими. Этот случай можно рассматривать как разветвление одной ударной волны на две1). Легко видеть, что наряду с двумя уходящими ударными волнами должен возникнуть еще и один расположенный между ними тангенциальный разрыв Od, разделяющий потоки газа, протекшего соответственно через Ob или Ос2). Действительно, волна Оа возникает от посторонних причин и потому является полностью заданной. Это значит, что имеют определенные заданные значения термодинамические величины (скажем, р, р) и скорость v в областях 1 и 2. Поэтому в нашем распоряжении остаются всего две величины — углы, определяющие направления разрывов Ob и Ос. С их помощью, однако, вообще говоря, нельзя удовлетворить четырем условиям (постоянство р, р и двух компонент скорости) в области 3—4, которые требовались бы при отсутствии тангенциального разрыва Od. Введение же последнего уменьшает число условий до двух (постоянство давления и направления скорости).
Разветвиться может, однако, отнюдь не произвольная ударная волна. Приходящая ударная волна определяется (при заданном термодинамическом состоянии газа 1) двумя параметрами, например, числом Mi натекающего потока и отношением давлений р\/рг. Разветвление оказывается возможным лишь в определенной области плоскости этих двух переменных3).
•)
Следует отметить, что разветвление
ударной волны на одну ударную же волну
и одну волну разрежения невозможно
(без труда можно убедиться в том, что
при таком пересечении нельзя было бы
согласовать друг с другом изменения
давления и изменения направлений
скорости в обеих исходящих волнах).
2)
Как всегда тангенциальный разрыв в
действительности размывается в
турбулентную область.
')
Определение этой области связано с
громоздкими алгебраическими или
численными расчетами. Повторим лишний
раз о необходимости следить при этом
за «направлением» ударных волн. Случаи,
в которых имелись бы две приходящие и
одна уходящая ударные волны представлял
бы собой пересечение двух разрывов,
возникающих от посторонних причин и
потому приходящих к месту пересечения
с заданными значениями всех параметров.
Их слияние в одну волну возможно лишь
при вполне определенном соотношении
между этими произвольными параметрами,
что являлось бы невероятной
случайностью.
 В
первом случае столкновение двух ударных
волн приводит к возникновению двух
ударных же волн, исходящих из точки
пересечения. Выполнение всех необходимых
условий снова требует возникновения
тангенциального разрыва, расположенного
В
первом случае столкновение двух ударных
волн приводит к возникновению двух
ударных же волн, исходящих из точки
пересечения. Выполнение всех необходимых
условий снова требует возникновения
тангенциального разрыва, расположенного
между уходящими ударными волнами.
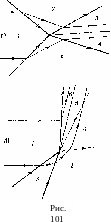
Во втором случае вместо двух ударных волн возникают одна ударная волна и одна волна разрежения.
Две сталкивающиеся ударные волны определяются тремя параметрами (например, М, и отношениями pi/p2, Р\1рг). Описанные типы пересечений возможны лишь в определенных областях значений этих параметров. Если же значения параметров лежат вне этих областей, то до столкновения ударных волн должно произойти их разветвление.
Рассмотрим, далее, типы пересечений, которые могут возникнуть при падении ударной волны на тангенциальный разрыв.
На рис. 102, а изображено отражение ударной волны от границы раздела между движущимся и неподвижным газами. Область 5 есть область неподвижного газа, отделенная от движущегося газа тангенциальным разрывом. В обоих граничащих с нею областях / и 4 давление должно быть одинаковым (равным р5). Поскольку же в ударной волне давление возрастает, то ясно, что она должна отразиться от тангенциального разрыва в виде волны разрежения 3, понижающей давление до первоначального значения. В точке пересечения тангенциальный разрыв терпит излом.
Пересечение ударной волны с тангенциальным разрывом, по другую сторону которого скорость жидкости отлична от нуля, но дозвуковая, вообще невозможно. Действительно, в дозвуковую область не могут проникнуть ни ударная волна, ни волна разрежения; поэтому в дозвуковой области может быть только тривиальное течение с постоянной скоростуо, так что тангенциальный разрыв не может иметь излома. Отражение ударной волны в виде волны разрежения невозможно, так как это неизбежно вызвало бы излом тангенциального разрыва; отражение в виде ударной волны тоже невозможно, поскольку при этом нельзя было бы удовлетворить условию равенства давлений на тангенциальном разрыве.
Если же течение по обе стороны тангенциального разрыва сверхзвуковое, возможны две различные конфигурации. В одном случае (рис. 102, б) наряду с падающей на тангенциальный разрыв ударной волной возникают еще и отраженная и преломленная ударные волны; тангенциальный разрыв терпит излом.

6) »)
• Ударная
вша
Тангещиапьный разрыв
Слабый разрыв
Линия тока
Рис. 102
В другом случае (рис. 102, в) возникают отраженная волна разрежения и прошедшая в другую среду преломленная ударная волна. Обе эти конфигурации возможны только в определенных областях значений параметров падающей ударной волны и тангенциального разрыва1).
Взаимодействие двух тангенциальных разрывов может привести к конфигурации без приходящих»ударных волн, а лишь с двумя уходящими (что невозможно, как было указано выше, в отсутствии тангенциальных разрывов). В области / на рис. 103 газ покоится; конфигурация возможна, очевидно, лишь при сверхзвуковом течении в областях 2 и 5.
Остановимся кратко на пересечениях ударной волны с приходящим от постороннего источника слабым разрывом. Здесь могут представиться два случая в зависимости от того, является ли движение за ударной волной сверх- или дозвуковым. В первом случае (рис. 104, а) слабый разрыв преломляется на ударной волне, проходя в пространство позади нее (сама же ударная волна в точке пересечения излома не имеет; ее форма имеет лишь особенность более высокого порядка —того же характера,
') Эти две конфигурации в известноу смысле обобщают случаи, изображенные на рис. 100 и 101,6.
что и особенность на слабом разрыве). Кроме того, изменение энтропии в ударной волне должно привести к возникновению позади нее еще и слабого тангенциального разрыва, на котором испытывают скачок производные энтропии.


Рис. 103 Рис. 104
логарифмической особенностью). Кроме того, как и в предыдущем случае, позади ударной волны возникает слабый тангенциальный разрыв энтропии.')
Сказанное относительно взаимодействия ударных волн со слабым разрывом справедливо и для взаимодействия со слабыми тангенциальными разрывами. Если течение в области за ударной волной сверхзвуковое, в ней возникают слабый и слабый тангенциальный разрывы. Если же течение за ударной волной дозвуковое, то в нем возникает лишь преломленный слабый же тангенциальный разрыв.
Наконец, упомянем еще о взаимодействии слабых разрывов с тангенциальными. Если течение по обе стороны тангенциального разрыва сверхзвуковое, наряду с падающим возникают отраженный и преломленный слабые разрывы. Если же течение по другую сторону тангенциального разрыва дозвуковое, слабый разрыв в него не проникает, происходит «полное внутреннее отражение» слабого разрыва.
') Детальное количественное исследование пересечений ударных волн со слабыми разрывами дано Дьяковым С. Л.— ЖЭТФ, 1957, т. 33, с. 948, 962.
