§ 105. Произвольное одномерное движение сжимаемого газа

Рассмотрим теперь общую задачу о произвольном одномерг ном изэнтропическом движении сжимаемого газа (без ударных волн) и покажем прежде всего, что эта задача может быть све­дена к решению некоторого линейного дифференциального урав­нения.

Всякое одномерное движение (движение, зависящее всего от одной пространственной координаты) непременно потенциально, так как всякую функцию v (x,t) можно представить в виде про­изводной v(х, t) = д<р(х, t)/dx. Поэтому мы можем воспользо,-ваться в качестве первого интеграла уравнения Эйлера уравне­нием Бернулли (9,3):

ir + -_- ^{+ a,==0}-

С помощью этого равенства получаем для дифференциала d(p: d<V = ^dx + ^dt = vdx — (-у- + w) dt.

Независимыми переменными являются здесь х и t; произведем теперь переход к новым независимым переменным, выбрав в ка­честве таковых v и w. Для этого производим преобразование Лежандра; написав

dy = d(xv) — xdv — d[t + + td {w +-if) и введя вместо потенциала qp новую вспомогательную функцию X = Ф — *» + /(а» + 4")'

получаем:

dx = — х dv + td (а> + =tdw + (vt — x) dv,

где % рассматривается как функция от v и w. Сравнив это соот­ношение с равенством d% = -4^- dw -f- ^r^dv, имеем:

ИЛИ

_t==lL _x===vJtL_^L (105 П

dw ' dw dv v » /

Если функция %(v, w) известна, то по этим формулам опреде­лится зависимость к и к от координаты х и времени t.

Выведем теперь уравнение, определяющее %. Для этого исхо­дим из неиспользованного еще уравнения непрерывности

dp , д , _ч др . др . dv „

-|_Г+_Ж(Р«)=_Ж+^+Р_Ж-=0.

Преобразуем это уравнение к переменным v, ш. Написав частные производные в виде якобианов, имеем:

д(р, х) д (г, р) д (/, у) ___ _п

d(t, х) ¹ д (t, х) д (t, х)

или, умножая на d(t, х)/d(w, v):

д(р,х) д (/, р) .a (t, v) q

<Э (а>, о) ' д (да, и) ~" 5 (да, о)

При раскрытии этих якобианов надо иметь в виду следующее. Согласно уравнению состояния газа плотность р есть функция каких-либо двух других независимых термодинамических вели­чин; например, можно рассматривать р как функцию от w и s. При s = const тогда будет просто р = р(ш); существенно при этом, что в переменных v, w плотность оказывается не завися­щей от v. Раскрывая якобианы, получаем поэтому

dp дх dp dt , dt ~

dw dv dw dv dw

Подставляя сюда для / и х выражения (105,1), получаем после сокращений:

р dw V dw dv² J ' . dw¹ При s = const имеем dw = dp/р. Поэтому можно написать

dp dp dp p

dw dp dw c² '

Окончательно получаем для % следующее уравнение:

(скорость звука с надо рассматривать здесь как функцию от и>). Задача об интегрировании нелинейных уравнений движения приведена, таким образом, к решению линейного уравнения.

Применим полученное уравнение к политропному газу. Здесь с⁸ (у—\)w, и основное уравнение (105,2) принимает вид

Это уравнение может быть проинтегрировано в общем виде элв- к 3-_Y

ментарным образом, если число _ | является целым четным числом:

7^Г = 2,г, Y = |r¥f- " = 0, 1, 2 (105,4)

Этому условию как раз удовлетворяют одноатомный (у = 5/3, и = 1) и двухатомный (у = 7/5, п = 2) газы. Вводя я вместо у, переписываем (105,3) в виде

Будем обозначать функцию, удовлетворяющую этому урав­нению при заданном я, посредством %_п- Для функции %₀ имеем|

^2w oV^ + ^T^⁰-

Введя вместо да переменную u — -y/2w, получаем:

д²Хо д²Хо ди² dv²

Но это есть обычное волновое уравнение, общее решение кото­рого есть: хо = Ы" + f)+ /г(и — у), где fi, /₂ — произвольные функции. Таким образом,

Xo = fi(V2a^-) + f_a(V2i»-o). (105,6)

Покажем теперь, что если известна функция %„, то функцию Хл+1 можно получить простым дифференцированием. В самом деле, дифференцируя уравнение (105,5) по ш, получаем после перегруппировки членов:

2 _£L (_дХ«Л , 2/г + З д ( дхп \ _ (дхп\ _ _п

2п+\ ^w dw² \ dw J ^ 2п+\ dw \ dw ) do² \ dw ) ^U"

Если ввести вместо v переменную

, /2ге + 3

^v = ^с'V^+T¹

то получим для d%_n/dw уравнение

_ _w JL (J2__\ + JL fJ____) -ЛГ-^) = о,

2 (re + 1) + 1 dw² \ dw ) dw \ dw J dv'² \ dw J

совпадающее с уравнением (105,5) для функции %_n+i(w, v'). Та­ким образом, мы приходим к результату, что

Применяя эту формулу п раз к функции (Ю5,6), получаем искомое общее решение уравнения (105,5):

ЗС = (fi (л/2(2я+ 1)ш + v) + /2 (л/2(2я+ 1)ш - v)},

или

_%т- fFiW2{2n+l)w + v)+_F₂W2(2n+l)w-v)) _g,

dwⁿ~^l \ Уда У

где Fi, ^2 — снова две произвольные функции. Если ввести вместо до скорость звука согласно

с² 2п + 1 о

то решение (105,8) примет вид

Х-(тк)""{7М«+*ПП-) + 7'.(«--ЯТт)}- ^,,05'⁹» Выражения

о v — 1

стоящие в качестве аргумента в произвольных функциях, пред­ставляют собой не что иное, как инварианты Римана (104,3), постоянные на характеристиках.

В применениях часто возникает необходимость в вычислении значений функции %(v, с) на характеристике. Для этой цели слу­жит следующая формула¹):

_{f-E-Y-'j-L/ffe±—Е_^)\ -Ц- '<* + «>, (,05,10)}

') Проще всего эту формулу можно вывести с помощью теории функций комплексного переменного, используя теорему Коши. Для произвольной функ­ции F{c -\- и) имеем:

/ д F(c + u) ^

V с дс ) с

_{= 2}-> f а Ч- + _{= 2}„-! <n-l)l * MV£+«)_ V дс² J с 2т j у₂ (z — с²)^п

где интеграл берется в плоскости комплексного переменного z по контуру, охватывающему точку г = с^г. Положив теперь и «= с + а и произведя в ин­теграле подстановку -д/'г =2? — с, получим:

!£ + ■ .

1 («-DI £ ^ +

где теперь контур интегрирования по £ охватывает точку £ = с; снова при­меняя теорему Коши, находим, что этот интеграл совпадает с написанным в тексте выражением.

_{\cdcj \с V 2n+lJ) 2""}¹ _дс"-¹ _с^{п v} _'

при

с + а

(а — произвольная постоянная).

Д==-

Выясним теперь, в каком взаимоотношении с найденным здесь общим решением газодинамических уравнении находится решение, описывающее простую волну. Последнее отличается тем свойством, что в нем v и w являются определенной функцией друг от друга, v = v(w), и поэтому обращается тождественно в нуль якобиан

д (a, w)

д (х, t)

Между тем при преобразовании к переменным v, w нам при­шлось разделить уравнение движения на этот якобиан, в резуль­тате чего решение, для которого Д = 0, оказалось потерянным. Таким образом, простая волна не содержится непосредственно в общем интеграле уравнений движения, а является их особым интегралом.

Для понимания природы этого особого интеграла существен­но, однако, что он может быть получен из общего интеграла пу­тем своеобразного предельного перехода, тесно связанного с фи­зическим смыслом характеристик как линий распространения малых возмущений. Представим себе, что область плоскости v, w, в которой функция %(v, w) отлична от нуля, стягивается к очень узкой в (пределе — к бесконечно узкой) полосе вдоль одной из характеристик. Производные от х в поперечных к характери­стике направлениях пробегают при этом значения в очень широ­ком (в пределе — бесконечном) интервале, поскольку % очень быстро убывает в этих направлениях. Такого рода решения %(v,w) уравнений движения заведомо должны существовать. Действительно, рассматриваемые как «возмущение» в плоскости v, w они удовлетворяют условиям геометрической акустики и, как должно быть для таких возмущений, расположены вдоль характеристики.

Из сказанного ясно, что при такой функции у_и время t = = d%/dw будет пробегать сколь угодно большой интервал зна­чений. Производная же от % вдоль характеристики будет неко­торой конечной величиной. Но вдоль характеристики (например, одной из характеристик Г_) имеем:

dJ— j 1 dp dw j 1 dw q

dv pc dw dv с dv

Поэтому производная от % no v вдоль характеристики (обозна* чим ее как —f(v)) есть

d%_ __дг iJlLJlE. —4- ri2L f (_r,\

dv да ~ dw dv dv dw ^{1 yyh}

Выражая частные производные от х через х и t согласно (105,1), получим отсюда соотношение x = (v + c)t + f(v), т. е. как раз уравнение (101,5) простой волны. Соотношение же (101,4), уста­навливающее связь между у и с в простой волне, автоматически выполняется в силу постоянства /_ вдоль характеристики Г_

В § 104 было показано, что если в некоторой части плоскости х, t решение уравнений движения сводится к постоянному те­чению, то в граничащих с нею областях должна иметься простая волна. Поэтому движение, описывающееся общим решением (105,8), может следовать за постоянным движением (в частно­сти, за областью покоя), лишь через промежуточную стадию простой волны. Граница между простой волной и общим реше­нием, как и всякая граница между областями двух аналитически различных решений, есть характеристика. При решении различ­ных конкретных задач возникает необходимость в определении значения функции %(w,v) на этой граничной характеристике.

Условие сшивания простой волны с общим решением на гра­ничной характеристике получается подстановкой выражений (105,1) для х и t в уравнение простой волны x—(v±c)t-\-+ f(v); это дает

#±.£₊„„_о.

Кроме того, в простой волне (и на граничной характеристике) имеем:

, , dp . dw или ±с — dw/dv. Подставив это в написанное условие, получим:

dv ⁺ dw dv dv ^v'

откуда окончательно

% = -\f(v)dv, (105,11)

чем и определяется искомое граничное значение %. В частности, если простая волна центрирована в начале координат, т. е. / (у) = 0, то х = const; поскольку функция х вообще определена лишь с точностью до аддитивной постоянной, то в этом случае можно, не уменьшая общности, положить на граничной харак­теристике х = 0.

Задачи

1. Определить движение, возникающее при отражении центрированной волны разрежения от твердой стенки.

Решение. Пусть волна разрежения возникает в момент / = 0 в точке t = 0 1 распространяется в положительном направлении оси х; она дойдет

при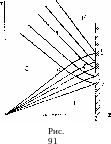

до стенки через промежуток времени t = l/со, где I — расстояние до стенки. На рис. 91 изображена диаграмма характеристик для процесса отражения волны В областях 1 я 1' газ неподвижен, в области 3 движется с постоян­ной скоростью v =*—U¹). Область 2 есть падающая волна разрежения (в прямолинейными характеристиками С+), а 5 — отраженная волна (с пря­молинейными характеристиками С_). Область 4 есть «область взаимодей­ствия», в которой должно быть най­дено решение; попадая в эту область, прямолинейные характеристики иск­ривляются. Это решение вполне оп­ределяется граничными условиями на отрезках аЬ и ас. На ab (т. е. на стенке) должно быть v — О при х = I; ввиду (105,1) имеем отсюда условие

в = 0.

Граница же ас с волной разрежения есть отрезок характеристики С_; по­этому на нем

у — 1 v

2п+ 1

dv

■ const,

а поскольку в точке а имеем v ««= 0, с — со, то const = со. На этой границе должно быть х = 0, так что имеем условие

*~° ^при 5ГТТ*^Св-

Легко убедиться в том, что функция вида (105,9), удовлетворяющая этим условиям, есть

/(2л+1) / д \»^-1PlY о V 2l"\

чем и определяется искомое решение.

Уравнение характеристики ас есть (см. задачу § 103)

2п+1

15

■ (2я + 1) <у + 2 (я + 1) /(JSa.)⁵*"⁷

Ее пересечение с характеристикой Ос

2(я+1) ~^С°~ 2я+1

U

to

определяет момент исчезновения падающей волны:

п + \

Д2п+1)^я+Ч

[(2п + I) с₀ ~ U]

На рис. 91 предполагается, что U < 2с₀/(у+ 1); в противном случае ха­рактеристика Ос направлена в сторону отрицательных х (рис. 92). Процесс

') Если волна разрежения возникает от поршня, который начинает вы­двигаться из трубы с постоянной скоростью, то U есть скорость поршня.

взаимодействия падающей и отраженной волн длится при этом бесконечное (а не конечное, как на рис. 91) время.

Функция (I) описывает также и взаимодействие двух одинаковых цен­трированных волн разрежения, вышедших в момент времени t = 0 из точек к <== 0 и х = 21 и распространяющихся навстречу друг другу, как это оче­видно из соображений симметрии (рис. 93) ').

Рис. 92 Рис. 93

2. Вывести уравнение, аналогичное уравнению (105,3), для одномерного изотермического движения идеального газа.

Решение. Для изотермического движения в уравнении Бернулли вме­сто тепловой функции w стоит величина

Sdp 2С ^rfP 2, „

где с\ = (др/др)_т — квадрат изотермической скорости звука; у идеального газа в изотермическом случае с_т — const. Выбрав эту величину (вместо ш) в качестве независимой переменной, получим тем же способом, что и в тексте, для функции х следующее линейное уравнение с постоянными коэффициен­тами:

2 д²Х , дХ_ _ д²% _ _п ^Ст др.^{2 +} d|i dv²