§ 63. Эффект де Гааза — ван Альфена

Магнитная восприимчивость металла в слабых магнитных полях (Bfi<^7\ В—магнетон Бора, В—магнитная индукция) не может быть вычислена в общем виде. Дело в том, что в рамках теории ферми-жидкости можно рассматривать только парамагнитную (спиновую) часть восприимчивости: эта часть определяется электронами проводимости вблизи ферми-поверх­ности, поскольку спины электронов в глубине распределения взаимно скомпенсированы. В диамагнитную же (орбитальную) часть восприимчивости вносят вклад все электроны, в том числе из глубины распределения, где понятие квазичастиц в теории ферми-жидкости уже теряет смысл. Между, тем обе части вос­приимчивости, вообще говоря, одного порядка величины, а ре­альный физический смысл имеет только их сумма.

Обратимся к «сильным» полям, когда

Т^В5<^р, (63,1)

^J) Фактически кристаллические решетки всех металлов обладают центром инверсии.

2) Ср. V § 60, где этот эффект рассматривался для идеального электрон­ного газа.

т. е. интервалы между уровнями Ландау сравнимы с темпера­турой, но все еще малы по сравнению с химическим потенциа­лом. В этом случае пара- и диамагнитная части намагничен­ности вообще не могут быть разделены, но здесь ситуация меняется в том отношении, что в намагниченности металла появляется осцилляционная зависимость от напряженности поля (эффект де Гааза—ван Альфена)²). Монотонная часть намагни­ченности и здесь зависит от всех электронов в металле и не может быть вычислена в рамках теории ферми-жидкости. Осцил­лирующая же часть намагниченности определяется, как мы увидим, лишь электронами проводимости в окрестности ферми-поверхности и может быть рассмотрена в общем виде (И. М.Лиф-шиц, А. М. Косеет, 1955). Именно эта часть и будет интере­совать нас здесь.

Осцилляционная зависимость намагниченности от поля яв­ляется следствием квантования уровней энергии орбитального движения электронов. Но квантованию подвергаются только состояния, отвечающие движению электронов по замкнутым (в k-пространстве) траекториям. Поэтому вклад в осцилляцион-ную часть термодинамических величин возникает только от электронов проводимости на замкнутых сечениях изоэнергети-ческих поверхностей плоскостями, перпендикулярными заданному направлению поля. Мы будем считать, что на этих сечениях выполняется условие квазиклассичности, т. е. что определяе­мые равенством (62,8) числа п велики:

heSl\e\B^>\. (63,2)

Для типичных ферми-поверхностей в металлах линейные раз­меры сечений ~1/а, так что S~a~², и тогда условие (63,2) заведомо выполняется (ср. примечание на стр. 279).

Квазиклассические уровни даются (с учетом спина) выра­жением (62,9), где е„(/г_г) — решения уравнения (62,8); каждому уровню отвечает число состояний, даваемое формулой (58/10). Поэтому статистическая сумма, определяющая термодинамичес­кий потенциал Q (функция р, Т и объема V системы), имеет вид

Индекс s нумерует отдельные листы изоэнергетической поверх­ности; этот индекс и знак суммирования по нему ниже для краткости опускаем. Интегрирование по dk_z производится по такому интервалу, чтобы в него были включены все различные (т.. е. за исключением их периодических повторений) сечения всех листов изоэнергетических поверхностей.

Прежде всего выделим из Q осциллирующую с полем часть (обозначим ее Й), преобразовав сумму (63,3) с помощью фор­мулы Пуассона¹):

Первый член этой формулы, примененной к (63,3), дает неос-циллирующий вклад в Q; опустив его, пишем

/=1а=±1

где Iia—осциллирующая часть интеграла

СО

I_la = j dn j In 11 + exp e™^iln dk₂. (63,6)

0

и введено также обозначение р_а = Р—o6£J3.

Для дальнейшего преобразования введем функцию

"(в,^)=^с-|т7р¹-Т (⁶³>⁷>

(ср. (62,8)) и перейдем от интегрирования по dn в (63,6) к ин* тегрированию по d&:

со

h =jjln{l+exp^|e^|^de; (63,8)

о

выбор нижнего предела интегрирования по de (условно поло­женного равным нулю) безразличен, так как в интеграле все равно будет существенна лишь окрестность значения е = р„.

Поскольку функция 'n(e, k_z) велика, экспоненциальный мно­житель в подынтегральном выражении в (63,8) —быстро осцил­лирующая функция k_z. Эти осцилляции погашают интеграл по dk_z, и потому основной вклад в него возникает от тех областей переменной k_z, в которых функция я(е, k_z) меняется наиболее медленно (так что и осцилляции наиболее медленны). Другими словами, основной вклад в интеграл дают области вблизи то­чек экстремумов п как функции от k_z (при каждом заданном е). Пусть k_zex(e)—одна из таких точек; вблизи нее вычисляем интеграл методом перевала: в показателе экспоненты пишем

n(e, k_z)&n_tx(e) + j(?^^(k— k_zexy, n_ex(e)=n(e, &_гех(е)),

а в неэкспоненциальных множителях берем их значение при К — Кех- В результате найдем, что каждая из экстремальных точек дает в интеграл вклад

_{П +"»*ИЪFrlSt"'}^ир _{К * *} *•}

замена дп (е, &_г)/3е на dn_eJdz допустима, поскольку в точке экстремума dnjdk₂ = 0. Знаки + или — в показателе экспонен­ты относятся соответственно к случаям, когда k_zsx является точкой минимума или максимума функции п (е, k₂)^х). Преобра­зуем это выражение интегрированием по частям, написав

ехр (2ш7л_ех) ds = ~d ехр (2га7я_ех (е))

и учитывая, что медленно меняющуюся функцию \d²n/dkl\_ex мож­но не дифференцировать. Проинтегрированный член не приводит к осцилляционной зависимости от поля; опустив его, имеем

7 V ^e±inli Г ехр(2я«Яех)Дв _{/ftq m}

lex

где суммирование производится по всем экстремальным точкам (смысл которых будет еще обсужден ниже).

Множитель ехр(2ш'/п_ех) в числителе подынтегрального выраже­ния—быстро осциллирующая функция е. Эти осцилляции по­гашают интеграл по de везде, за исключением области &—Цо~Т, в которой быстро меняется знаменатель. Сама же функция п_ех (е) в этой области меняется плавно и потому может быть представ­лена в виде

"ех (б) « «ех (И-а) + "ех (Ца) (е — Ца);

множитель же |д²л/д£²,|₁Г_х^1/2 просто заменяется его значением при е = |л₀. После этого, перейдя от интегрирования по е к интег­рированию по х = (е—]x_a)jT и заменив нижний предел —ц_а/Т на —со (поскольку u./r^>l), получим²)

^г) Перевальный интеграл вида ^ e^!az' dz вычисляется путем замены

z = ue^lIt-'⁴ или г = ие~'^Я/'⁴ при а > 0 или а < 0, после чего интегрирование по d« распространяется от —оо до оо. ²) Использовано значение интеграла

е^1аг . in

■dz = -

е^г -f- 1 sh яа

Эту формулу можно получить, рассмотрев интеграл по замкнутому контуру в плоскости комплексного г, составленному из вещественной оси, прямой 1тг = 2я и двух бесконечно удаленных «боковых» отрезков (для обеспечения сходимости на последних вещественный параметр а заменяем на а —1'0). Ин­теграл по этому контуру определяется вычетом в полюсе z = m, откуда нахо­дим /—_е-^2яа/ = — 2я«е-^яа.

- _v ехр [2я«7л_ех (Иа) ± ⁽'«/4] ,

При суммировании этого выражения по а = ± 1 можно везде (кроме экспоненциального множителя) заменить р_а на р, по­скольку по предположению (63,1) 6В<^р. В фазовом же (экспо­ненциальном) множителе такая замена недопустима: ввиду большой величины функции п_ех(е) уже относительно малое из­менение ее аргумента приводит к заметному изменению фазы; здесь, однако, достаточно разложить п_ех(Р±рВ) по степеням 6В, ограничившись линейными членами. В результате получим

ехр [2niln_ex (ц.) ± in/4]

х

X sh-^l[2n²/7n;_x(p)]cos[2n/6B|_exn;_x(p)], (63,10)

где H_ex = £(6zex)- Остается выяснить смысл входящих в это выражение величин и подставить его в (63,5).

Согласно определению (63,7), функция п_ех (е) связана с экстре­мальным значением 5_ех (е) площади сечения изоэнергетической поверхности 5 (е, k_z) как функции k₂, а ее значение при е = р есть площадь экстремального сечения ферми-поверхно­сти. Для иллюстрации на рис. 15 изо­бражены экстремальные (два максималь­ных и одно минимальное) сечения ган-телеобразной ферми-поверхности; они пер­пендикулярны направлению поля, указан­ному стрелкой. Суммирование по ех в (63,10) производится по всем экстремальным замкнутым сечениям всех листов ферми-поверхности. Мы введем также, для упрощения записи формул, циклотронную массу электрона проводимости при его движении по экстремальной замкнутой траектории. Согласно определению (57,6), эта масса

2n

d&

fa dS (е, k_z) | _ fa , >

"2^ ^ех W,

пг =

In. k

где S_ex(e) = S(e, k_zex(e)); последнее равенство снова связано с тем, что в точке экстремума 6\S(e, k_z)jdk_z = Q.

В результате приходим к следующей окончательной формуле для осциллирующей части термодинамического потенциала:

^соз(я7^Ц|, (63,11)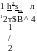

Q = 2S (-l)'Q/cos

a»S(n, k_z)\

ex / = 1

dki

q ₌ 2У(тЩ^Ь12

^l~ „7/2 *З_т./

Я = 1п*Тт*/т$В

(т—истинная масса электрона, знаки + или —в аргументе косинуса относятся соответственно к случаям минимальных или максимальных сечений)¹).

Намагниченность М (магнитный момент единицы объема) вычисляется как производная²)

М = -1§§. (63,12)

При этом дифференцированию в (63,11) должны подвергаться лишь наиболее быстро меняющиеся множители — косинусы. Ввиду анизотропии ферми-поверхности (т* и 5_ех зависят от направления поля) направление М не совпадает, вообще говоря, с направлением В. Для осциллирующей части продольной (в направлении поля) намагниченности находим

ех

Выражения (63,11) и (63,13)—сложные осциллирующие функции магнитного поля, причем они содержат, вообще говоря, члены различной периодичности: члены, происходящие от каж­дого из экстремальных сечений ферми-поверхности имеют свой

^{6Q = <6Я> = - -1 J <j> 6А dV.}

мент, по onpej >лучим

бй = — бВ ^ MdV,

Введя теперь магнитный момент, по определению <j> = с rot М, и произведя интегрирование по частям, получим

эффект де гааза — ван альфена

423

период по переменной 1/5, равный

Отметим, что эти периоды не зависят от температуры.

Температурная же зависимость амплитуд осцилляции опреде­ляется множителем X/sh Я. При X ^> 1 амплитуды убывают экс­поненциально, и осцилляции фактически исчезают. При множитель X/shX~l, и порядок величины амплитуд опреде­ляется остальными множителями в Q, и М^, к этому случаю и относятся все последующие оценки.

Для грубой оценки положим

т* ~т, p. ~ fakp/tn, S ~ k_F,

где k_P~\/a—линейные размеры ферми-поверхности. Тогда по­лучим

й-к^-иЦИ)". Л~_лР(М)"\ (вэ.19

где n~kp — плотность числа электронов. Что же касается мо­нотонно зависящей от поля части намагниченности (обозначим ее М), то ее можно оценить, положив

'М~хВ~р^В~прШ, (63,16)

где х—«монотонная» часть магнитной восприимчивости, оценен­ная, например, по формуле для восприимчивости электронного газа в слабых полях (см. V § 59). Соответственно монотонная часть термодинамического потенциала й ~ VMB~VnyL (ВВ/р,)². Сопоставление написанных выражений показывает, что осцилли­рующая часть термодинамического потенциала мала по сравне­нию с его монотонной магнитнЪй частью:

Й/5~(ВВ/|1)»/*<^1,

и тем более—по сравнению с его значением Q₀~Vn\L в отсут­ствие поля: Q/fi₀ ~ (6Б/р)⁵/². Осциллирующая же часть нама­гниченности, напротив, велика по сравнению с ее монотонной частью

(11/рЯ)«/а^1.

По поводу всей изложенной теории осцилляции намагничен­ности следует отметить, что она относится к электронной жид­кости в идеальном кристалле, и в ней не учитывается возможное влияние на эффект, процессов рассеяния электронов проводи­

мости на фононах и на дефектах решетки (например, на атомах примесей). Эти процессы приводят к неопределенности в энергии электронов: Аг~%/т ~hv_P/l (где т — время между столкновениями; /—длина свободного пробега; v_F—скорость электронов). Размытие же резких уровней энергии приводит, в свою очередь, к сглаживанию осцилляции намагниченности.

Условие допустимости пренебрежения про- Н цессами рассеяния состоит в малости не-

определенности Ае по сравнению с интер­валами между уровнями, т. е. должно быть:

_А-У

ftw_B^hv_F/L (63,17)

r\^Ji При Т—*0 допустимы (условием (63,1))

е сколь угодно малые значения В (точнее—

ограниченные лишь условием (63,17)). При

~_д этом намагниченность М может, в прин-

_{Рис ]6} ципе, стать сравнимой с самой индукцией

В (так как М/В ~ % (fx/pS)'/²-), но еще раньше становится большой (по модулю) магнитная восприимчивость % = дМ/дН*). Действительно, снова заметив, что дифференциро­ванию должны подвергаться только осциллирующие множители, найдем

|Х|~Х((л/РЯ)³/². (63,18)

В такой ситуации осцилляции намагниченности приводят к появлению на кривой зависимости макроскопической напря­женности Н = В — 4лМ (В) от индукции В ряда последователь­ных перегибов, как это показано схематически на рис. 16 (А.В. Pippard, 1963). Но условие термодинамической устойчи­вости требует, чтобы было²)

™) >0.

дВ Jt.vl^