§ 15. Двухчастичная функция Грина

К другим важным понятиям диаграммной техники мы при­дем, рассмотрев усредненное по основному состоянию Т-про-изведение четырех гейзенберговских о|з-операторов *):

*„,_й = <ттдда?>. (15,1)

Эту функцию называют двухчастичной функцией Грина (в отли­чие от функции Грина (7,9), называемой в этой связи одно-частичной).

Для применения теории возмущений и построения диаграм­мной техники надо снова перейти к ^-операторам в представ­лении взаимодействия. Как и в случае функции G, это приве­дет к появлению множителя S под знаком Т-произведения: •

Кз4,₁₂ = ^г_Г<ТФ„зад⁺₁П₂5>. (15,2)

В нулевом приближении (т.е. при 5 = 1) это выражение распа­дается на сумму произведений двух сверток, выражающихся через С⁽⁰⁾-функции:

Kiln = GM - Gg?G2». (15,3)

Дальнейшее обсуждение свойств определенной таким обра­зом двухчастичной функции Грина будем проводить в импуль­сном представлении.

Для однородной системы функция K_Si, is зависит фактически лишь от трех независимых разностей аргументов, например, от Х₃—Х₂, Х₄—Х₂, Х_г—Х₂. В импульсном представлении это свойство выражается тем, что компонента разложения Фурье по всем переменным X_it Х₄ содержит б-функцию:

j К_и, _i2exp {i(P,X, + P₄X₁-P_IX_i-/>₁X₁)}<Wf_i.. .d*X_f =

= {2nyo^(P₃ + P_i-P₁-P₂)K_y6,_af_i(P₃, P_t\ Pi, P_t). (15,4) В этом легко убедиться, заметив, что Р зХ₃ + Р₄Х₄— P₁X_i — P₂X₂ —

= Р₃ (Х₃-Х₂) + Р₄ (Х₄—Х₂)—Р_х (Х-Х₂)-Х, {Р, + Р₂-Р₃-Р₄),

*) Мы снова применяем упрощенные обозначения, где индексы 1, 2, ... обозначают совокупности 4-координат и спинового индекса: Х_га, Л"₂р\ ... (ср. примечание на стр. 66). В полной записи

К34, is = Куй, ав (-^8> Х₄; Xf, Xj),

и перейдя к интегрированию по Х₃—Х₄, Х₄—Х₂, X_t — X₂, Х₂. Отметим, кстати, что формулу обратного фурье-преобразования

можно записать как

(15,5)

Определенную таким образом функцию К_у&, а$(Рз>^Р1< ^ри ^Рг) мы и будем называть двухчастичной функцией Грина в импульс­ном представлении; ее аргументы связаны равенством

P. + P^Ps + P,.

В нулевом приближении имеем для нее (в соответствии с (15,3))

_{=*(2") V}⁽_{«' (К-К) G?i (Рх) GW*)-*}^w_{(Pi-Pt) Gy% (P,) G}⁽_{ia (Pi)],}

(15,6)

т. е. К сводится к сумме двух произведений одночастичных гриновских функций.

В следующих приближениях теории возмущений появляются члены, сводящиеся к введению поправок к этим одночастичным функциям.^ Наряду с ними, однако, возникают также и члены, не укладывающиеся в произведения G-функций. Именно эта часть двухчастичной функции Грина представляет самостоятель­ный интерес. Для ее выделения представим К. в виде

Ка^. «,«, (Рг, P_t\ Pi, P_t) = (2я)« [6⁽⁴⁾ (Я_г-Р_а) G_a^ (Рг) G^P,) -- 8<« {Pi~P_t) Ga₃a₂ (Л) G«_tai (Рг)] +

+ ОалЛ^р₃)ОалЛ^р*)Лм₁, р.рЛЛ, Л; ^ри Л)0_Э1в1(^) Gp,_a, (я,).

(15,7)

Определенную таким образом функцию Г называют вершинной функцией.

Согласно определению (15,1), двухчастичная функция Грина в пространственно-временном представлении антисимметрична по отношению к перестановкам аргументов (вместе со спино­выми индексами) первой и второй пары: 1 и 2 или 3 и 4. От­сюда следует аналогичное свойство симметрии для функции Грина и вершинной функции в импульсном представлении:

Г₇б, ар (Р₃, Р«; Pi, P_t) = - r_6v, _ар (P., Р₃\ Pi, P_t) =»

= -Tyt.fia(P_a,P_tlP_t,P₁). (15,8)

Смысл выделения четырех G-множителей в определении Г (последний член в (15,7)) становится ясным, если проследить за характером диаграмм, возникающих при раскрытии выра­жения (15,2) для двухчастичной функции Грина. Следующие ниже рассуждения снова предполагают парное взаимодействие между частицами.

В нулевом приближении функции К сопоставляются ди­аграммы

Р =Р Р — Р

^г i — ^г 2 ^r 8 — ^Г 2

отвечающие двум членам в (15,6). В первом порядке теории возмущений появляются диаграммы типов ^х)

представляющие собой поправки к каждому из отдельных мно­жителей в (15,6). Кроме них, однако, появляются также ди­аграммы, не разбивающиеся на две отдельные части:

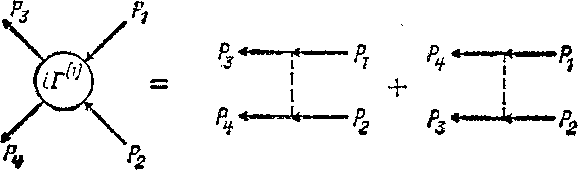
(15,9)

Четыре стрелки Р_± Р₄ отвечают четырем G-множителям в

последнем члене в (15,7), а «внутренняя» часть диаграмм опре­деляет (в первом порядке) вершинную функцию—кружок в ле­вой стороне диаграммного равенства (15,9). Раскрыв эти ди­аграммы в аналитическом виде, получим

Г%«э(^з. Р₄; Pi, /⁵2) = -S_av6_R6c/(P₁-P₃) + 6_a66p_v(7 (Pi-P₄).

Диаграммы более высоких порядков содержат поправки трех категорий: 1) дальнейшие поправки к двум не соединенным между собой сплошным линиям, 2) поправки собственно-энер­гетического типа к концевым линиям на диаграммах (15,9), 3) поправки, образующие фигуру, заменяющую собой пунктир­ную линию на диаграммах (15,9); сумма всех возможных таких

^J) Как и в случае одночастичной функции Грина, множитель <S>^-1 в определении (15,2) приводит к исчезновению диаграмм, содержащих отсоеди­ненные замкнутые петли сплошных линий.

§ 15]

ДВУХЧАСТИЧНАЯ ФУНКЦИЯ ГРИНА

79

(15,10)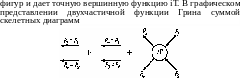

жирные линии изображают точные G-функции, а кружок условно обозначает вершинную функцию.

Вычисление вершинной функции в различных порядках тео­рии возмущений должно производиться по сформулированным в § 13 правилам диаграммной техники, причем должны рас­сматриваться диаграммы с четырьмя внешними концами (а не с двумя, как при вычислении G). Правило 3), определяющее общий знак диаграммы, должно быть дополнено следующим указанием: если непрерывными последовательностями сплошных линий связаны концы 1 с 4 и 2 с 3 (вместо 1 с 3 и 2 с 4), то знак диаграммы меняется на обратный.

Изобразим, для примера, все диаграммы, определяющие вер­шинную функцию во втором порядке теории возмущений:

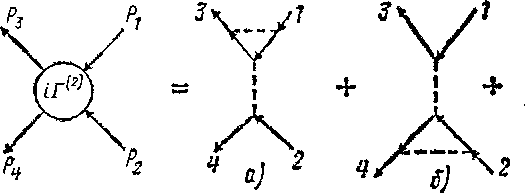
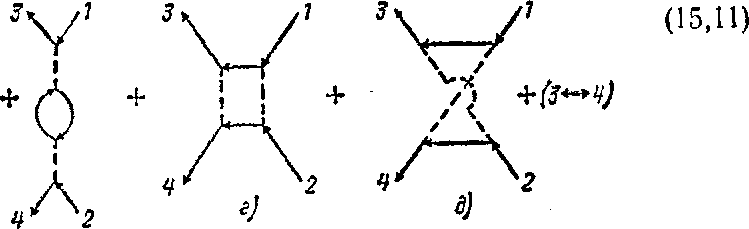
*) Оно аналогично уравнению Дайсона в квантовой электродинамике (см. IV § 104).

Собственно-энергетическая и вершинная функции (2 и Г) не независимы; они связаны друг с другом определенным инте­гральным уравнением (так называемым уравнением Дайсона)¹).

Для его вывода воспользуемся уравнением (9,5), справед­ливым (как было отмечено там же) и при учете взаимодействия частиц. Разница по сравнению с выводом в § 9 состоит, однако, в том, что теперь г|)-оператор удовлетворяет уравнению (7,8). Опустив в последнем член с внешним полем и подставив из него производную dW/dti .в (9,5), получим

('1г ⁺ 2^ ⁺ ^^0ар(Х"^Х2)~^{базб<4> (Х}*~^Х*⁾⁼⁼

=- i [(ту; (х_а) и (Xi - х,) % (х₃) d*x, ■ w_a (x_f) Щ (х₂))=

^{=— t. 5 Kya, vp (X}₃^{, Xi, X}₃^,X₂^)U _i3^d*X₃^{. (15,12)}

Это равенство решает, в принципе, поставленный вопрос, так как К выражается через Г согласно (15,7). Остается лишь пе­рейти к импульсному представлению. Для этого умножим ра­венство (15,12) на exp[iP (Х — Х₂)] и проинтегрируем по dⁱ(X_i — Х₂), представив /С₃₁-,_зг в виде (15,5), a U₁₃ в виде (13,9). Тогда интегрирование по 4-координатам дает б-функции, кото­рые устраняются интегрированием по 4-импульсам. В резуль­тате получим

_[0(о,-_1(/)₎₀₍р₎_₁]_бар==

Л; р₃+р*-р,Р)и(р-рУ-^?± (15,13)

с G^m(P) из (9,7).

Теперь осталось выразить К через Г. Подставив (15,7) в (15,13), получим окончательно уравнение Дайсона в виде

баз [С'⁰'"¹ (P)-G-¹ (Р)] = б_ар2 (Р) =

= U (0) п (ц) б_ар + i8_an j UiP-PJ G (PJ -|^- +

+ J r_va. vp (P_s ,Pi, Р₃+Р*-Р,Р)0 (P₃) G (P_t) G (P₃ +P,-P)X

хи(Р-РУ^0^. (15,14)

Здесь n(p) — точная плотность системы как функция ее хими­ческого потенциала; этот множитель возникает от интегриро­вания G-функции по формуле (7,24) (при этом учитывается, что данная G-функция возникла от свертки, в которой Ч^г+ стоит слева от Ф). Отметим, что первый член в правой стороне урав­нения (15,14) есть 2_а (14.11).