X) Чтобы не разбивать изложения, доказательство этой теоремы отложиы на конец параграфа.

3 Е. М. Лифшнц, л. П. Питаевскнй

— 00

Для большей компактности записи формул введем обозначение U (Хх-Хз) = U (_Г1-г₂) б (13,4)

Тогда!)

где dⁱX = dtd³x.

Чтобы усреднить по теореме Вика, выпишем отдельно опе­раторы и изобразим все нужные варианты сверток:

Согласно сказанному выше, опущены члены, содержащие свертку ^4<J • Попарно сворачиваемые (соединенные дугами) операторы надо переставить к соседству друг с другом. Так, первый из написанных членов означает произведение

<гвд> <w+¥₄> <твд>,

а последний

- <W.f ₄⁺> < ТВД>

Свертки произведений ^-операторов различных аргументов за­меняются согласно

4yF₃⁺ s (тад⁺>= , Ч^4 = -/^4 и т.п.

Свертки же -ф-операторов одинаковых аргументов представляют собой пространственную плотность числа частиц в идеальном газе (обозначим ее через п⁽⁰⁾), понимаемую как функцию хими­ческого потенциала²):

*) Здесь и ниже для упрощения записи особенно громоздких выражений с ловимся опускать индекс у ¥₀, а цифровыми индексами 1, 2, ... обозначать совокупность значений аргумента X и спинового индекса:

²) Такие свертки всегда происходят от т^-операторов, входящих в состав одного и того же оператора взаимодействия V. Поэтому в таких членах ¥+ всегда стоит слева от W■

_<У⁺_{У> = п»>(ц)= °У • (13,5)}

Таким образом, получим

Ш% = | J d*X, d*X_x • U _м[- G<°₃>G№> - GJOTGS>+

+ W^e>Gi?Gg) + fn<°>Gi?Gff].

Эти четыре члена попарно равны друг другу — они отличаются лишь обозначением переменных интегрирования Х₃ и Х₄. В ре­зультате множитель 1/2 исчезает и, таким образом, поправка первого порядка в функции Грина содержит всего два члена:

Структуру этих членов удобно изобразить графически с по­мощью следующих диаграмм Фейнмана:

Юй> = $ ^ulin^MV-G^G^X.d^X,. (13,6)'

5 hoi

гра

Q

< ^!< и < ■ (13,7)

14 2 1 3 4 2 ^v

На этих диаграммах сплошная линия 4<—2 означает свертку

YiWt (т. е. функцию tG₄?); цифры указывают номера перемен­ных Х₄ и Х₂, от которых зависят свертываемые операторы, а направление стрелки отвечает направлению от Ч*^-"¹" к W в свертке.

Свертка двух операторов, зависящих от одних и тех же

переменных (т. е. плотность n^W)), изображается соответственно петлей—сплошной линией, «замкнутой на себя». Пунктирная

линия 3 4 означает множитель U_3i. По всем переменным,

обозначенным у внутренних точек диаграммы (точки пересече­ния линий), подразумевается интегрирование. Переменные (X_t и Х₂), обозначенные у «внешних концов» диаграммы, остаются свободными.

Члены первого порядка, происходящие из (13,3), изобрази­лись бы диаграммами, распадающимися на две отдельные ча­сти— прямой отрезок (t'G„p) и фигуру с замкнутыми петлями сплошных линий, например,

Вдумавшись в способ свертывания операторов и структуру со­ответствующих диаграмм, можно понять происхождение обще­го правила: во всех порядках теории возмущений роль множи­теля <5>~¹ в (12,14) сводится к тому, что должны учитывать­ся лишь «связные» диаграммы с двумя внешними концами, не содержащие «отсоединенных» петель без внешних концов, не связанных с другими частями диаграммы ни сплошными, ни пунктирными линиями (ср. аналогичную ситуацию в квантовой электродинамике —IV § 100).

Сокращение коэффициента 1/2 в (13,6) есть проявление об­щего правила: не надо учитывать (в членах n-го порядка) мно­житель 1/п!, происходящий от разложения (13,1), и множитель 2~^в, возникающий от коэффициентов 1/2 в (13,2). Действительно, диаграммы n-го порядка содержат по п пунктирных линий

i k. Множитель 1/п! сокращается от приведения членов,

отличающихся перестановками пар чисел i, k между всеми п пунктирными линиями. Множитель же 2~^п сокращается от пе­рестановок чисел i, k между концами каждой из этих линий.

Окончательные правила диаграммной техники мы сформу­лируем для вычисления функции Грина не в координатном, а сразу в импульсном представлении, наиболее важном для физи­ческих применений.

Переход к импульсному представлению осуществляется путем разложения Фурье (7,21—22), которое запишем в «четырехмер­ном» виде^J)

G{X)=^G{P)e~^^, G(P)=$G(X)*™d*X, (13,8)

где «4-импульс» Р = (со, р), a PX = &t—рг. Аналогичным обра­зом разложим также и потенциал взаимодействия:

U (X) =3 (0 U{r) = $U (Q) е-^-Ц , (13,9)

где Q— (q_Q, q); при этом U (Q) совпадает с компонентой трех­мерного разложения

^{U(Q) = U(q) = J U(r)e-^d4. (13,10)}

Ввиду четности функции U (г) очевидно, что U (—q) = t7(q).

Произведем это разложение для поправки первого порядка Gi2=G2p(Xj — Х₂). Для этого умножаем равенство (13,6) на exp[iP(X_f—Х₂)] и интегрируем его по dⁱ(X_i — Х₂).

В первом члене пишем

_eiP (х,-х₂) _{= е}1Р &_±-Х,)_е(Р (Х_а-Х_г)

^]) Используя для удобства изложения и обозначений четырехмерную тер­минологию, подчеркнем 'лишний раз, что она не имеет здесь никакого отно­шения к релятивистской инвариантности!

и, заменив переменные интегрирования, получаем in^m J G^(X₁-X₃)e^№№-^)^(X_i-X₃)x X S G% (X₃-X_t) d* (X₃-X_t) J U (X₃-X_t) d'(X_a-X,).

Первые два интеграла дают G^_y(P)G_y%(P), а третий равен 1/(0) = ^ U (г) d³x—значению U (q) при q = 0. Аналогичным образом, во втором члене пишем

_eiP (X, -X,) _ glP {X_t -X,) _eiP (X_t- X,) glP (X,-Х_г)

и после перехода к интегрированию по Xf—Х₃, Х₃—Х₄, Х₄—Х_а получаем

^{- G$ (Р) S G$ (X) (У (X) eipx d*X • Gel (P).}

Оставшийся интеграл выражается через фурье-компоненты функ­ций С$5 и U с помощью формулы для фурьё-компонент произ­ведения двух функций*)

^f(X)g(X)e^dⁱX = ^f(P₁)g(P-P_i)-^. (13,11)

Таким образом, для поправки первого порядка в функции Грина в импульсном представлении окончательно находим

iG§ (Р) = in»» U (0) G«_y (Р) G$ (Р) -

-J G<»> (Р) G$ (Р,) G$(P) (7 (p-_Pl) @. (13,12)

Каждому из двух членов в (13,12) ставится в соответствие определенная диаграмма Фейнмана, и выражение (13,12) запи­сывается в виде

₉

<М* ! + ЛА (13,13)

р«—^—р

а) а)

^г) Для доказательства этой формулы надо подставить в ее левую сторону сами функции }(Х) и g(X) в виде фурье-разложений:

J / (X) g (X) d*X = $f (К) g (P.) ^(P ^'"^ * d*X ^p-. чтегрирование no d^lX осуществляется по формуле

^e^ipxdⁱX = (2n)ⁱ6W(P),

где «четырехмерная» б-функция 6<⁴> определяется как произведение б-функ« ций от компонент «4-вектора» Р. Возникающий множитель 6<⁴>(Р—Pi~P%) устраняется интегрированием по d*Pz, и мы приходим к правой сторон* (13,11).

Точки пересечения линий называют вершинами диаграммы. Каждая диаграмма имеет 2п вершин, где п—порядок теории возмущений. В каждой вершине сходятся две сплошные и одна пунктирная линии. Каждой сплошной линии приписывается свой «4-импульс» Р в направлении, указанном стрелкой (при­чем вдоль каждой непрерывной последовательности сплошных линий направление стрелок не меняется). Каждой пунктирной линии приписывается 4-импульс Q, причем и для этих линий условно выбирается какое-либо (любое) направление стрелки ¹). В вершинах диаграммы выполняется «закон сохранения 4-им-пульса»: сумма 4-импульсов входящих линий равна сумме 4-им-пульсов выходящих из вершин линий. Вершине приписывается также и определенный спиновый индекс а. Каждая диаграмма имеет две внешние линии (входящую и выходящую), 4-импульс которых есть аргумент искомой функции Грина G_ag(P); выхо­дящей и входящей внешним линиям приписываются также спи­новые индексы аир этой функции. Остальные линии диаграммы называют внутренними.

Аналитическая запись членов, отвечающих каждой диаграм­ме, производится по следующим правилам:

1. Каждой сплошной линии между вершинами аир ста­вится в соответствие множитель t'G„^(P), каждой пунктирной линии—множитель —Ш (Q). Замкнутой петле с одной верши­ной сопоставляется множитель п⁽⁰⁾(р:).

2. В каждой вершине выполняется закон, сохранения 4-им-пульса. По остающимся неопределенными 4-импульсам внутрен­них линий производится интегрирование по сКР/(2я)⁴. В каждой вершине производится суммирование по паре немых спино­вых индексов — по одному от каждого из соседних С^<0)-множи-телей.

3. Общий множитель, с которым диаграмма входит в t'G_ap, равен (—\)^L, где L—число содержащихся в ней замкнутых петель сплошных линий с более чем одной вершиной.

Здесь все свертки равны iGl₂\ iGk-i, ь а последняя равна

*) «Временные» компоненты 4-векторов Q = (<7o> ч)> вообще говоря, отлич­ны от нуля, но функция U (Q), по определению (13, 10), от q₀ не зависит. Условность направления пунктирной линии связана с четностью функции U(-Q) = U(Q).

Последнее правило имеет следующее происхождение. Замкну­тая петля с k > 1 вершинами происходит от свертки 1|з-опера-торов вида

— iGkl- Что касается петель с одной вершиной, то их правиль­ный знак учитывается уже введением п^т по правилу 1.

Для примера изобразим совокупность диаграмм, определя­ющих поправку второго порядка в функции Грина:

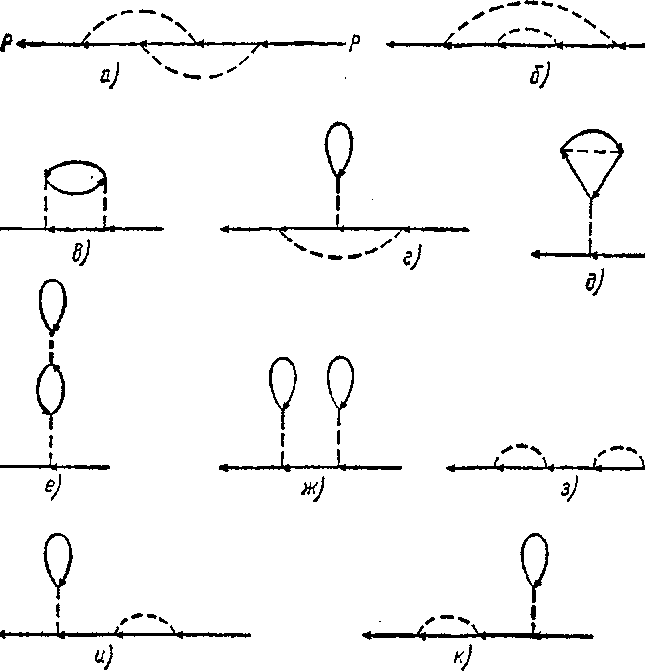
(13,14)

Наконец, вернемся к теореме Вика и дадим ее доказатель­ство в применении к «макроскопическому пределу» (т. е. при V —*- со или, что то же при заданной плотности системы, при N—^со), который только и существен в статистических при­менениях.

Рассмотрим, например, среднее от произведения четырех ^-операторов типа

<%№А> = ут £ <a_Pla_P2a_p⁺₃a_P⁺₁>exp(...) (13,15) pi •■■ Pi

(ф-операторы представлены в виде (9,3); очевидные, но громозд­кие показатели экспонент не выписываем). В этой сумме отличны от нуля лишь члены, в которых содержится по одинаковому числу операторов а_р и а_р с одинаковыми значениями импуль­сов. Среди них есть члены, в которых импульсы равны попарно, например, _Pl = p₄ и р₂ = р₃. Эти члены отвечают попарной

свертке

и выражаются суммой вида

"т/г £ <flp₁flp⁺,><ep.flp.> ^ехР (•••)•

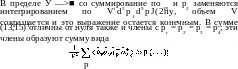но после перехода в ней к интегрированию один множи­тель 1/V остается, и в пределе V—> со выражение обращается в нуль.

Ясно, что этот результат имеет общий характер: в пределе V—>оо в среднем значении от произведения гр-операторов не обращаются в нуль лишь результаты попарных сверток.

Отметим, что в изложенном доказательстве по существу не использовалось, что усреднение производится именно по основ­ному состоянию, и поэтому оно остается справедливым и при усреднении по любому квантовому состоянию системы¹).